图像预处理笔记

目录

• 1. 图像的显示与存储原理
  • 1.1 颜色空间
  • 1.2 存储
• 2 图像增强的目标
  • 2.1 点运算：基于直方图的对比度增强
  • 2.2 形态学处理
  • 2.3 空间域处理：卷积 CNN （平滑、边缘检测、锐化等）
  • 2.4 频率域处理：傅里叶变换、小波变换

1. 图像的显示与存储原理

1.1 颜色空间

RGB颜色空间
加法混色，越叠加越亮（白）
3个通道 RGB，一个图片数据有3维，长宽和通道，立方体色彩空间
一个像素的颜色值 (b,g,r)
取值范围
[0, 255], 归一化后 [0.0, 1.0]

CMY（K） 颜色空间
减法混色，越叠加越黑
4个通道, 青，品红，黄，黑。 CMY为立方体色彩空间
一个像素颜色值 (c, m, y, k)
取值范围
[0, 255], 归一化后 [0.0, 1.0]

HSV颜色空间
人类视觉概念比较接近，用于画家配色操作
3个要素 Hue 色调，颜色种类；Saturation 饱和度，颜色的纯度，Value 明度，颜色明亮度。圆椎形的色彩空间，下顶点是黑色，中间向上是黑到白的渐变，上面越往圆的边缘颜色纯度越高，圆一周是不同种类的颜色
一个像素颜色值 (h, s, v) 可以与 RGB 进行转换
取值范围
([0, 255]), 归一化后 ([0.0, 1.0])

CIE－XYZ颜色空间
国际照明协会1931基于人类颜色视觉感知的直接测定，对颜色的感知不均匀，比如对蓝色的区分种类要比绿色多出很多
用于摄影

1.2 存储

RGB 三通道彩色图 存储为 3维空间，包含3个2维单通道 (([0, 255]))
灰度图 转换方法例如 (Gray = R*0.3 + G*0.59 + B*0.11)

2 图像增强的目标

预处理的目标是图像增强。
让你看的更清晰，该看的东西能看到。转换为更适合人或机器分析处理的形式。突出对人或机器分析有意义的信息比如色差很小，让色差变化大一点，有层次更容易看到有用的东西。或者让光线均匀等，无意义的东西就是噪声去掉。还有灰度调整主要是对比度增强。
其实就是更方便算法处理和分析，能够得到更有意义的结果

深度学习数据增强是训练时样本不够造数据。人脸识别训练时如果样本不够，采用原图翻转的方法增加数据应该是数据增强而不是图像增强。

• 图像处理方法
  • 空间域处理
    • 点运算 － HE CLAHE，基于直方图对整体色差调整，每个点色彩的调整跟周围或多或少还是有点关系
    • 形态学运算 - 膨胀、腐蚀
    • 临域运算 - 每个点跟周围点比较或者一块进行运算，卷积、金字塔
  • 频率域处理
    • 傅里叶变换 - 为了快速计算空间域上的卷积，空间域上的卷积是频率域上的乘，乘完作逆变换
    • 小波变换 - 哈尔小波

2.1 点运算：基于直方图的对比度增强

对点的灰度或者颜色等进行统计直方图，然后使用统计上的 bin划分，每个 bin 区间上出现的灰度的频数

直方图均衡化
光线不均匀的图，进行非线性的拉伸。每个 bin 区间内的直方图的累加，使得 bin 之间的累积值大致相等。但是为什么？在统计上有什么意义？

如果光线特别不均匀，有的地方特别亮或者特别暗，可以先做局部直方图均衡，具体地来说固定块区域做直方图均衡然后按特定步长滑动依次做直方图均衡。每个点得到多次赋值后求平均值。即自适应直方图均衡 AHE

AHE 却可能把相对均匀区域的噪声给放大。CLAHE方法进行修剪掉高的部分，把整个直方图垫高。直方图均衡赋值的时候考虑相邻块的灰度，以保证颜色的过渡较连续。如果得到的图还是突兀，得到的图可以与原图做混色，每个像素点可以与原图相加取平均值进行滤色混合。

2.2 形态学处理

沿着边， A-B 腐蚀。B 沿着 A 的边添加是膨胀。
先腐蚀再膨胀，去掉目标外的孤立点。先膨胀，去掉目标内的孔。

2.3 空间域处理：卷积 CNN （平滑、边缘检测、锐化等）

[sumlimits_{k,l} I(x+k, y+l)f(k,l)＝h(x,y) ]

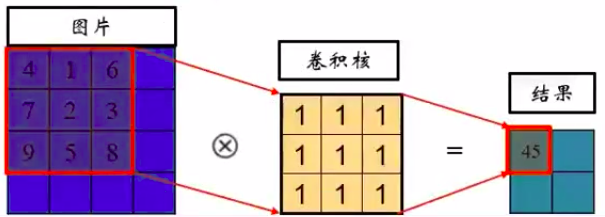
(f(k,l)) 是卷积核，扫描窗，与原图对应位置相乘，然后对结果相加，然后得到的值给 x,y 所在的位置上。这里传统的卷积核是经验。深度学习的卷积核是学习出来的。

边界填充 补零用的比较多。但也不能太多，所以不要用大卷积核处理小区域。边界复制。是否可以对矩阵左边界与右边界循环卷积？ 或者把右端填充左边界等，也是可以的。

均值滤波
扫描窗内求平均值。缺陷是没有很好地去噪声，也破坏了细节。让图像模糊。平均值的通病? 既解决不了outlier又掩盖细节。

中值滤波 对原图区域像素排序，取中间值。就是中位数？统计中中位数可以解决均值的缺点。简单的滤波方法里，中值滤波效果比较好。

高斯滤波 模拟人眼，关注中心区域。参数卷积参数坐标x,y和标准差(sigma)。滤波处理的图像与原图叠加。关注中心的区域更加清晰，其它区域模糊。类似人眼

[G_{sigma}(x,y)=frac{1}{2pi sigma^2}e^{-frac{x^2+y^2}{2sigma^2}} ]

(sigma)越小关注区域越集中，与高斯分布比较对应。(sigma)越大关注区域越大，整个图越模糊。模糊图用于高斯金字塔。场景，给定一个看起来很远很远造成模糊的图，保留哪些像素能够接近原图。用高斯滤波一层层处理效果比较好。高斯滤波更多的用于构建高斯金字塔。

平滑高斯滤波
一个(m imes m) 的图像，卷积核 (k imes k) 步长为 (n)，时间复杂度为 ((m^2 imes k^2)/(n imes n))。二维卷积拆分成两个相同的一维卷积，列卷积和行卷积。对卷积核进行拆分，可以减少计算，二维为 (k imes k) 次计算，一维卷积为 (2k) 次计算

[frac{1}{2pi sigma^2}e^{-frac{x^2+y^2}{2sigma^2}}=left(frac{1}{sqrt{2pi sigma^2}}e^{-frac{x^2}{2sigma^2}} ight)left(frac{1}{sqrt{2pi sigma^2}}e^{-frac{y^2}{2sigma^2}} ight) ]

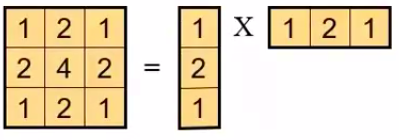
梯度滤波
Prewitt
垂直边缘检测，使用水平方向有明显变化如 -1 0 1 而垂直方向均值平滑的卷积核。水平边缘检测使用垂直方向有明显变化而水平方向均值平滑的卷积核。

Sobel
使用高斯代替上面的均值平滑，允许在另一个方向上有高斯变化

Laplacian
二阶微分算子，导数极值 (Delta=frac{partial^2f}{partial x^2}+frac{partial^2f}{partial y^2})

对于边缘检测，像素值快速变化的区域
对于团块的检测，找到一个点明显高于或才低于周边的像素点

卷积核要求所有值和为0。这样能保证不会检测出完全光滑的区域，如果完全光滑的区域，像素值都一个与卷积核运算结果也为0

这个卷积方法能够找到图像中的细节，与原图叠加后，能使原图的细节够清晰，实现锐化。

其它锐化滤波，先卷积一个突出的部分，再减去平均的部分，使细节更突显。

其它

PCA 降维是用的矩阵分解。卷积一般不算是降维。卷积和张量，卷积核要跟被卷积图像匹配得了。

卷积维度降低是保留重要特征，把不重要的去掉了。

彩色图像滤波一层一层的做，做完再合起来。

2.4 频率域处理：傅里叶变换、小波变换

空间域卷积＝频率域乘积。可以使计算更快。
高斯金字塔
图像变小，如果直接下采样，图像过度会很不好。比如四个像素只取一个值。损失信息比较多。
先做平滑高斯滤波(变模糊(高斯模糊))再做降采样。这样降采样变小的图像柔和很多。模糊但是柔和，就是图像过度比较好。

目标检测，目标可能是在图像上较大的部分，也可能是较小的部分。高斯金字塔逐级降采样的过程，在大尺度上找小特征，在小尺度上找大特征。高斯金字塔本质上为信号的多尺度表示法。

拉普拉斯金字塔
高斯处理之后的图像 (G_{i+1})，进行上采样 UP((G_{i+1})otimes mathcal{G}_{k imes k})。与处理之前的图像 (G_i) 进行做差比较，得到采样丢失的细节 (L_i)。
(L_i=G_i-UP(G_{i+1})otimes mathcal{G}_{k imes k})
依次计算出来的 (L_i) 就是拉普拉斯金字塔。
(L_i) 用于图像恢复的时候进行叠加。有了最后的高斯金字塔处理后的小图，和拉普拉斯金字塔(L_i) 就可以恢复图像。反操作即可。对小图上采样然后高斯模糊，叠加拉普拉斯金字塔。最终能够恢复原图。上采样的方法是一个像素周围填充0，或者都取一样的值等方法。
(G_i=UP(G_{i+1})otimes mathcal{G}_{k imes k}+L_i)

频率域分析
傅里叶变换
任何一个信号波可以由足够多的不同的频率和幅值的正余弦波组成
(Asin(omega x) + B cos(omega x))
连续变换，波形的叠加

[F(omega)=intlimits_{-infty}^infty f(t)e^{-iomega t}mathrm{d}t ]

逆变换

[f(t)=frac{1}{2pi}intlimits_{-infty}^infty F(omega) e^{iomega t}mathrm{d} omega ]

离散傅里叶变换
离散傅里叶变换

[F(omega)=sumlimits_{t=-infty}^infty f_t e^{-omega t} ]

二维

[F(u, v)=sumlimits_{x=0}^{M-1}sumlimits_{y=0}^{N-1} f(x,y) e^{-i2pi(frac{ux}{M}+frac{vy}{N})} ]

对应到图像是由不同频率的条纹组成。规律：图像上连续，频谱上是离散的点。图像上离散，频谱上是很多的点。靠近圆点是频率低的，低通的，条纹间隔大的。越向外，是频率高的，高通的，条纹密的，是原图的细节部分。

还有相位滤波，频段滤波。

解决信号不平稳的方法，使用短时傅里叶加窗口，窗口内认为是平稳的。窗口过宽，能够知道频率，不好判断点在哪；窄了，知道点在哪个窗口，不能够了解频率。

规律：频率分辨率高的时候，时间分辨率低，反之变然

小波变换

Haar 小波用的比较多