二叉树的遍历 详解及实现

在之前的博文中我们讲解了二叉树的使用——《哈夫曼压缩》，那么，我们对于二叉树的操作不仅仅局限于创造，二叉树是一种储存处理方式，但是，我们不能仅仅是存储数据，那么，我们今天就来讲解一下从二叉树中读取数据的方法及操作。

二叉树的遍历方式有三种：
1.先根序：根 、左子树、右子树
2.中根序：左子树、根 、右孩子
3.后根序：左子树、右子树、根

现在通过一个例子来为，我让大家清晰了解们这三种遍历方法：

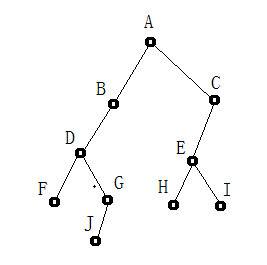
对于这个二叉树来说：
先根序遍历结果：A B D F G J C E H I
中根序遍历结果：F D J G B A H E I C
后根序遍历结果：F J G D B H I E C A

现在我们来构造一个二叉树，然后对这个二叉树进行遍历操作：
首先，我们按照我们之前博文中一直有的惯例，上手先编写"mec.h"：

#ifndef _MEC_H_
#define _MEC_H_

typedef unsigned char boolean;
typedef boolean u8;

#define TRUE		1
#define FALSE		0

#define NOT_FOUND		-1

#define SET(v, i) (v |= (1 << ((i) ^ 7)))
#define CLR(v, i) (v &= ~(1 << ((i) ^ 7)))
#define	GET(v, i) (((v) & (1 << ((i) ^ 7))) != 0)

#endif

之后，我们再来构建二叉树“单节点”结构体：

typedef struct BTREE {
	int data;
	struct BTREE *left;
	struct BTREE *right;
}BTREE;

那么，我们要构建二叉树，就要从键盘输入一个字符串，再读取字符串判断字符串输入是否合理，再根据正确的字符串构建二叉树。
而这里通过字符串构建二叉树就要用到我们之前的博文——《表达式的处理》以及《哈夫曼压缩》两篇博文中的知识了。
现在我们来规定下输入字符串的正确格式如下：
A(B,C)
A(B,)
A(,B)
A(B)
A(,)
A()

那么，要实现通过输入的字符串构建二叉树，就要通过字符串来画状态变迁图：
那么，根据状态变迁图，我们来用宏定义所有可能出现的状态：

#define BTREE_STATUS_BEGIN		1
#define BTREE_STATUS_END		2
#define BTREE_STATUS_ROOT		3
#define BTREE_STATUS_LEFT		4
#define BTREE_STATUS_RIGHT		5
#define BTREE_STATUS_COMMA		6
#define BTREE_STATUS_CHILD		7

现在我们来构建一个表示完整二叉树的结构体：

typedef struct BTREE_ARG {
	int status;				//这个成员表示当前节点的状态
	int index;				//这个成员表示遍历字符串时用的下标
	boolean ok;				//这个成员表示遍历到当前位置字符串表达是否正确
	boolean finished;		//这个成员用来表示字符串是否遍历到末尾
	BTREE *root;			//这个成员用来存储第一个节点的信息
	BTREE *tmp;				//这个成员用来表示当前的节点的信息
	boolean whichChild;		//这个成员用来表示当前节点为父节点的“左孩子”还是“右孩子”
	MEC_STACK *nodeStack;	//这个成员用来存储父节点的首地址
	int breaketMatch;		//这个成员用来表示括号是否匹配
}BTREE_ARG;

现在来编写一个宏表示“左孩子”还是“右孩子”，以满足上面结构体内whichChild成员的赋值：

#define LEFT_CHILD		0
#define RIGHT_CHILD		1

因为我们读取的字符串可能出现错误，所以我们采用《表达式的处理》那一篇博客中的处理方式——编写“mecErr.c”和“mecErr.h”:
mecErr.h:

#ifndef _MEC_ERROR_H_
#define _MEC_ERROR_H_

void showError();

#endif

mecErr.c:

#include <stdio.h>

#include "mecError.h"

const char *errMess;	//这个变量在我们根据字符串构建二叉树中会用到

void showError() {
	if (NULL == errMess) {
		printf("No Error!
");
		return;
	}
	printf("Error:%s
", errMess);
}

我们再来思考一下，因为我们要在遍历字符串遇到新的有效节点时访问它的父节点，以便使父节点的孩子指针指向新节点，所以，我们用到了堆栈的处理方法，因为我们在之前的博文中已经进行过讲解，所以，这里就直接将代码复制过来：
mecStack.h:

#ifndef _MEC_STACK_H_
#define _MEC_STACK_H_

#include "mec.h"

typedef struct MEC_STACK {
	void **stack;
	int capacity;
	int top;
}MEC_STACK;

boolean initStack(MEC_STACK **stack, int capacity);	//初始化堆栈   函数
void destoryStack(MEC_STACK **stack);				//销毁堆栈     函数
boolean isStackEmpty(const MEC_STACK *stack);		//判栈空       函数
boolean isStackFull(const MEC_STACK *stack);		//判栈满       函数
boolean push(MEC_STACK *stack, void *data);			//将数据入栈   函数
void *pop(MEC_STACK *stack);						//将数据出栈   函数
void *readTop(const MEC_STACK *stack);				//读取栈顶指针 函数

#endif

mecStack.c:

#include <stdio.h>
#include <malloc.h>

#include "mec.h"
#include "mecStack.h"

void *readTop(const MEC_STACK *stack) {
	if (NULL == stack || isStackEmpty(stack)) {
		return NULL;
	}
	
	return stack->stack[stack->top - 1];
}

void *pop(MEC_STACK *stack) {
	if (NULL == stack || isStackEmpty(stack)) {
		return NULL;
	}
	
	return stack->stack[--stack->top];
}

boolean push(MEC_STACK *stack, void *data) {
	if (NULL == stack || isStackFull(stack)) {
		return FALSE;
	}
	stack->stack[stack->top++] = data;
	
	return TRUE;
}

boolean isStackFull(const MEC_STACK *stack) {
	return stack != NULL && stack->top >= stack->capacity;
}

boolean isStackEmpty(const MEC_STACK *stack) {
	return stack != NULL && stack->top <= 0;
}

void destoryStack(MEC_STACK **stack) {
	if (NULL == stack || NULL == *stack) {
		return;
	}
	
	free((*stack)->stack);
	free(*stack);
	
	*stack = NULL;
}

boolean initStack(MEC_STACK **stack, int capacity) {
	MEC_STACK *res;
	
	if (NULL == stack || NULL != *stack || capacity <= 0) {
		return FALSE;
	}
	
	res = (MEC_STACK *) calloc(sizeof(MEC_STACK), 1);
	res->stack = (void **) calloc(sizeof(void *), capacity);
	res->capacity = capacity;
	res->top = 0;
	
	*stack = res;
	
	return TRUE;
}

那么，大体我们都准备好了，我们现在来编写根据字符串构建二叉树的函数：

boolean createBTreeByString(const char *str, BTREE **btree) {
	BTREE_ARG arg = {
		BTREE_STATUS_BEGIN, // int status;
		0,					// int index;
		TRUE,				// boolean ok;
		FALSE,				// boolean finished;
		NULL,				// BTREE *root;
		NULL,				// BTREE *tmp;
		LEFT_CHILD,			// boolean whichChild;
		NULL,				// MEC_STACK *nodeStack;
		0,					// int breaketMatch;
	};

	if (NULL == btree || NULL != *btree) {
		return FALSE;
	}

	initStack(&arg.nodeStack, strlen(str));					//这个初始化堆栈函数在上面编写的"mecStack.h"文件中声明

	while (arg.ok && !arg.finished) {
		arg.index += skipBlank(str + arg.index);			//跳过字符串中空格函数，我们在下面内容中进行编写
		if (BTREE_STATUS_BEGIN == arg.status) {
			dealBtreeStatusBegin(str[arg.index], &arg);		//处理开始状态函数，我们在下面内容中进行编写
		} else if (BTREE_STATUS_END == arg.status) {
			dealBtreeStatusEnd(&arg, btree);				//处理结束状态函数，我们在下面内容中进行编写
		} else if (BTREE_STATUS_LEFT == arg.status) {
			dealBtreeStatusLeft(str[arg.index], &arg);		//处理左括号状态函数，我们在下面内容中进行编写
		} else if (BTREE_STATUS_ROOT == arg.status) {
			dealBtreeStatusRoot(str[arg.index], &arg);		//处理根节点状态函数，我们在下面内容中进行编写
		} else if (BTREE_STATUS_COMMA == arg.status) {
			dealBtreeStatusComma(str[arg.index], &arg);		//处理小数点状态函数，我们在下面内容中进行编写
		} else if (BTREE_STATUS_CHILD == arg.status) {
			dealBtreeStatusChild(str[arg.index], &arg);		//处理孩子状态函数，我们在下面内容中进行编写
		} else if (BTREE_STATUS_RIGHT == arg.status) {
			dealBtreeStatusRight(str[arg.index], &arg);		//处理右括号状态函数，我们在下面内容中进行编写
		}
	}

	if (FALSE == arg.ok) {		// 要销毁生成了一半的二叉树中的节点！这就牵扯到二叉树的遍历了（这篇博文通过“后根序”方式实现）
		destroyBtree(arg.root);
		arg.root = NULL;
	}
	destoryStack(&arg.nodeStack);							//销毁堆栈函数，在上面编写的"mecStack.h"文件中声明

	return arg.ok;
}

那么，我们现在来编写处理各种状态的函数：
1.处理开始状态的函数：

void dealBtreeStatusBegin(int ch, BTREE_ARG *arg) {
	if (isalpha(ch)) {
		arg->root = arg->tmp = createOneNode(ch);
		++arg->index;
		arg->status = BTREE_STATUS_ROOT;
	} else {
		errMess = "出师未捷身先死";
		arg->ok = FALSE;
	}
}

2.处理结束状态函数：

void dealBtreeStatusEnd(BTREE_ARG *arg, BTREE **root) {
	if (arg->breaketMatch != 0) {						//因为我们等会遇到左括号会使这个变量加1，遇到右括号使这个变量减1，所以在结束时应该为0，而在我们处理右括号时会解决左括号缺失的问题，所以，这里只会是因为缺右括号
		errMess = "括号不匹配之缺少右括号";
		arg->ok = FALSE;
		return;
	}
	*root = arg->root;									//这里的赋值是为了等会在主函数中销毁整个二叉树
	arg->finished = TRUE;
}

3.处理左括号状态函数：

void dealBtreeStatusLeft(int ch, BTREE_ARG *arg) {
	if (isalpha(ch)) {
		processAlpha(ch, arg);							//处理字母函数，在之后代码中编写
	} else if (',' == ch) {
		processComma(arg);								//处理逗号函数，在之后代码中编写
	} else if (')' == ch) {
		processRightBracket(arg);						//处理右括号函数，在之后代码中编写
	} else {
		errMess ="非法字符!"
		arg->ok = FALSE;
	}
}

3.1.处理字母函数：

void processAlpha(int ch, BTREE_ARG *arg) {
	BTREE *parent;

	parent = (BTREE *) readTop(arg->nodeStack);
	if (arg->whichChild == RIGHT_CHILD && parent->right != NULL) {
		errMess = "孩子个数不满足要求！";
		arg->ok = FALSE;
		return;
	}
	
	arg->tmp = createOneNode(ch);					//创造新节点函数，在之后代码中编写
	if (LEFT_CHILD == arg->whichChild) {
		parent->left = arg->tmp;
	} else {
		parent->right = arg->tmp;
	}
	++arg->index;
	arg->status = BTREE_STATUS_CHILD;
}

3.1.1.创造新节点函数：

BTREE *createOneNode(int ch) {
	BTREE *res = calloc(sizeof(BTREE), 1);
	res->data = ch;
	res->left = res->right = NULL;

	return res;
}

3.2.处理逗号函数：

void processComma(BTREE_ARG *arg) {
	arg->whichChild = RIGHT_CHILD;
	++arg->index;
	arg->status = BTREE_STATUS_COMMA;
}

3.3.处理右括号函数：

void processRightBracket(BTREE_ARG *arg) {
	if (--arg->breaketMatch < 0) {
		errMess = "括号不匹配之缺少左括号!";				
		arg->ok = FALSE;
		return;
	}

	pop(arg->nodeStack);
	++arg->index;
	arg->status = BTREE_STATUS_RIGHT;
}

4.处理根节点状态函数：

void dealBtreeStatusRoot(int ch, BTREE_ARG *arg) {
	if ('(' == ch) {
		processLeftBracket(arg);				//处理左括号函数，在之后代码中编写
	} else if (0 == ch) {
		arg->status = BTREE_STATUS_END;
	} else {
		errMess = "非法字符!";
		arg->ok = FALSE;
	}
}

4.1.处理左括号函数：

void processLeftBracket(BTREE_ARG *arg) {
	arg->breaketMatch++;
	push(arg->nodeStack, arg->tmp);
	arg->whichChild = LEFT_CHILD;
	++arg->index;
	arg->status = BTREE_STATUS_LEFT;
}

5.处理小数点状态函数：

void dealBtreeStatusComma(int ch, BTREE_ARG *arg) {
	if (isalpha(ch)) {
		processAlpha(ch, arg);
	} else if (')' == ch) {
		processRightBracket(arg);
	} else {
		errMess = "非法字符!";
		arg->ok = FALSE;
	}
}

6.处理孩子状态函数：

void dealBtreeStatusChild(int ch, BTREE_ARG *arg) {
	if ('(' == ch) {
		processLeftBracket(arg);
	} else if (')' == ch) {
		processRightBracket(arg);
	} else if (',' == ch) {
		processComma(arg);
	} else {
		errMess = "非法字符!";
		arg->ok = FALSE;
	}
}

7.处理右括号状态函数：

void dealBtreeStatusRight(int ch, BTREE_ARG *arg) {
	if (',' == ch) {
		processComma(arg);
	} else if (')' == ch) {
		processRightBracket(arg);
	} else if (0 == ch) {
		arg->status = BTREE_STATUS_END;
	} else {
		errMess = "非法字符!";
		arg->ok = FALSE;
	}
}

8.跳过字符串中空格函数：

int skipBlank(const char *str) {
	int index;

	for (index = 0; str[index] && isspace(str[index]); index++) {
		;
	}

	return index;
}

那么，到目前位置，我们通过字符串构建二叉树的操作已经基本完成了，因为我们接下来的销毁不完整二叉树（字符串中间错误，构造了一半二叉树）和展示二叉树各节点储存的数值，就需要我们遍历二叉树，那么，现在我们来编写今天的主要讲解的内容——二叉树的遍历问题：

在上面我们将结果二叉树的遍历一共右三种最基本的形式：
先根序、中根序、后根序
那么，在编写展示二叉树各节点存储的信息时，我们将这三种方法都来实现一遍：
1.（先根序版）展示函数：

void travelFirstRoot(const BTREE *root) {
	if (NULL == root) {
		return;
	}
	printf("%c ", root->data);
	travelFirstRoot(root->left);
	travelFirstRoot(root->right);
}

2.（中根序版）展示函数：

void travelMiddleRoot(const BTREE *root) {
	if (NULL == root) {
		return;
	}
	travelMiddleRoot(root->left);
	printf("%c ", root->data);
	travelMiddleRoot(root->right);
}

3.（后根序版）展示函数：

void travelLastRoot(const BTREE *root) {
	if (NULL == root) {
		return;
	}
	travelLastRoot(root->left);
	travelLastRoot(root->right);
	printf("%c ", root->data);
}

以上的递归，可能有的同学觉得看不明白，这就需要同学们自己动手来跟着代码实现一遍，这样，就会更深一步理解这里递归函数的妙处了。

那么，在完成了一切操作之后，我们一定要记得销毁二叉树，否则会造成“内存泄漏”，浪费计算机内存！
现在来编写销毁二叉树函数：

void destroyBtree(BTREE *root) {
	if (NULL == root) {					//当根节点首地址为NULL时，则在上一次递归中完成了对叶子节点的释放（对于叶子节点知识不清楚的，请观看本人博文——《哈夫曼压缩》）
		return;
	}
	destroyBtree(root->left);
	destroyBtree(root->right);
	free(root);
}

那么，现在我们来总结一下我们今天所编写的工具函数：
btree.h:

#ifndef _MEC_B_TREE_H_
#define _MEC_B_TREE_H_

#include "mec.h"

typedef struct BTREE {
	int data;
	struct BTREE *left;
	struct BTREE *right;
}BTREE;

#define BTREE_STATUS_BEGIN		1
#define BTREE_STATUS_END		2
#define BTREE_STATUS_ROOT		3
#define BTREE_STATUS_LEFT		4
#define BTREE_STATUS_RIGHT		5
#define BTREE_STATUS_COMMA		6
#define BTREE_STATUS_CHILD		7

boolean createBTreeByString(const char *str, BTREE **btree);
void travelFirstRoot(const BTREE *root);
void travelMiddleRoot(const BTREE *root);
void travelLastRoot(const BTREE *root);
void destroyBtree(BTREE *root);

#endif

btree.c:

#include <stdio.h>
#include <ctype.h>
#include <string.h>
#include <malloc.h>

#include "mec.h"
#include "btree.h"
#include "mecStack.h"
#include "mecError.h"

void destroyBtree(BTREE *root) {
	if (NULL == root) {
		return;
	}
	destroyBtree(root->left);
	destroyBtree(root->right);
	free(root);
}

void travelLastRoot(const BTREE *root) {
	if (NULL == root) {
		return;
	}
	travelLastRoot(root->left);
	travelLastRoot(root->right);
	printf("%c ", root->data);
}

void travelMiddleRoot(const BTREE *root) {
	if (NULL == root) {
		return;
	}
	travelMiddleRoot(root->left);
	printf("%c ", root->data);
	travelMiddleRoot(root->right);
}

void travelFirstRoot(const BTREE *root) {
	if (NULL == root) {
		return;
	}
	printf("%c ", root->data);
	travelFirstRoot(root->left);
	travelFirstRoot(root->right);
}

typedef struct BTREE_ARG {
	int status;
	int index;
	boolean ok;
	boolean finished;
	BTREE *root;
	BTREE *tmp;
	boolean whichChild;
	MEC_STACK *nodeStack;
	int breaketMatch;
}BTREE_ARG;

#define LEFT_CHILD		0
#define RIGHT_CHILD		1

extern const char *errMess;			//这里extern表示是外部文件变量

static int skipBlank(const char *str);
static void dealBtreeStatusBegin(int ch, BTREE_ARG *arg);
static void dealBtreeStatusEnd(BTREE_ARG *arg, BTREE **root);
static void dealBtreeStatusLeft(int ch, BTREE_ARG *arg);
static void dealBtreeStatusRoot(int ch, BTREE_ARG *arg);
static void dealBtreeStatusComma(int ch, BTREE_ARG *arg);
static void dealBtreeStatusChild(int ch, BTREE_ARG *arg);
static void dealBtreeStatusRight(int ch, BTREE_ARG *arg);
static BTREE *createOneNode(int ch);
static void processAlpha(int ch, BTREE_ARG *arg);
static void processLeftBracket(BTREE_ARG *arg);
static void processRightBracket(BTREE_ARG *arg);
static void processComma(BTREE_ARG *arg);

static void processComma(BTREE_ARG *arg) {
	arg->whichChild = RIGHT_CHILD;
	++arg->index;
	arg->status = BTREE_STATUS_COMMA;
}

static void processRightBracket(BTREE_ARG *arg) {
	if (--arg->breaketMatch < 0) {
		errMess = "括号不匹配之缺少左括号!";
		arg->ok = FALSE;
		return;
	}

	pop(arg->nodeStack);
	++arg->index;
	arg->status = BTREE_STATUS_RIGHT;
}

static void processLeftBracket(BTREE_ARG *arg) {
	arg->breaketMatch++;
	push(arg->nodeStack, arg->tmp);
	arg->whichChild = LEFT_CHILD;
	++arg->index;
	arg->status = BTREE_STATUS_LEFT;
}

static void processAlpha(int ch, BTREE_ARG *arg) {
	BTREE *parent;

	parent = (BTREE *) readTop(arg->nodeStack);
	if (arg->whichChild == RIGHT_CHILD && parent->right != NULL) {
		errMess = "孩子个数不满足要求！";
		arg->ok = FALSE;
		return;
	}
	
	arg->tmp = createOneNode(ch);
	if (LEFT_CHILD == arg->whichChild) {
		parent->left = arg->tmp;
	} else {
		parent->right = arg->tmp;
	}
	++arg->index;
	arg->status = BTREE_STATUS_CHILD;
}

static BTREE *createOneNode(int ch) {
	BTREE *res = calloc(sizeof(BTREE), 1);
	res->data = ch;
	res->left = res->right = NULL;

	return res;
}

static void dealBtreeStatusRight(int ch, BTREE_ARG *arg) {
	if (',' == ch) {
		processComma(arg);
	} else if (')' == ch) {
		processRightBracket(arg);
	} else if (0 == ch) {
		arg->status = BTREE_STATUS_END;
	} else {
		errMess = "非法字符!";
		arg->ok = FALSE;
	}
}

static void dealBtreeStatusChild(int ch, BTREE_ARG *arg) {
	if ('(' == ch) {
		processLeftBracket(arg);
	} else if (')' == ch) {
		processRightBracket(arg);
	} else if (',' == ch) {
		processComma(arg);
	} else {
		errMess = "非法字符!";
		arg->ok = FALSE;
	}
}

static void dealBtreeStatusComma(int ch, BTREE_ARG *arg) {
	if (isalpha(ch)) {
		processAlpha(ch, arg);
	} else if (')' == ch) {
		processRightBracket(arg);
	} else {
		errMess = "非法字符!";
		arg->ok = FALSE;
	}
}

static void dealBtreeStatusRoot(int ch, BTREE_ARG *arg) {
	if ('(' == ch) {
		processLeftBracket(arg);
	} else if (0 == ch) {
		arg->status = BTREE_STATUS_END;
	} else {
		errMess = "非法字符!";
		arg->ok = FALSE;
	}
}

static void dealBtreeStatusLeft(int ch, BTREE_ARG *arg) {
	if (isalpha(ch)) {
		processAlpha(ch, arg);
	} else if (',' == ch) {
		processComma(arg);
	} else if (')' == ch) {
		processRightBracket(arg);
	} else {
		errMess = "非法字符!";
		arg->ok = FALSE;
	}
}

static void dealBtreeStatusEnd(BTREE_ARG *arg, BTREE **root) {
	if (arg->breaketMatch != 0) {
		errMess = "括号不匹配之缺少右括号";
		arg->ok = FALSE;
		return;
	}
	*root = arg->root;
	arg->finished = TRUE;
}

static void dealBtreeStatusBegin(int ch, BTREE_ARG *arg) {
	if (isalpha(ch)) {
		arg->root = arg->tmp = createOneNode(ch);
		++arg->index;
		arg->status = BTREE_STATUS_ROOT;
	} else {
		errMess = "出师未捷身先死!";
		arg->ok = FALSE;
	}
}

boolean createBTreeByString(const char *str, BTREE **btree) {
	BTREE_ARG arg = {
		BTREE_STATUS_BEGIN, // int status;
		0,					// int index;
		TRUE,				// boolean ok;
		FALSE,				// boolean finished;
		NULL,				// BTREE *root;
		NULL,				// BTREE *tmp;
		LEFT_CHILD,			// boolean whichChild;
		NULL,				// MEC_STACK *nodeStack;
		0,					// int breaketMatch;
	};

	if (NULL == btree || NULL != *btree) {
		return FALSE;
	}

	initStack(&arg.nodeStack, strlen(str));

	while (arg.ok && !arg.finished) {
		arg.index += skipBlank(str + arg.index);
		if (BTREE_STATUS_BEGIN == arg.status) {
			dealBtreeStatusBegin(str[arg.index], &arg);
		} else if (BTREE_STATUS_END == arg.status) {
			dealBtreeStatusEnd(&arg, btree);
		} else if (BTREE_STATUS_LEFT == arg.status) {
			dealBtreeStatusLeft(str[arg.index], &arg);
		} else if (BTREE_STATUS_ROOT == arg.status) {
			dealBtreeStatusRoot(str[arg.index], &arg);
		} else if (BTREE_STATUS_COMMA == arg.status) {
			dealBtreeStatusComma(str[arg.index], &arg);
		} else if (BTREE_STATUS_CHILD == arg.status) {
			dealBtreeStatusChild(str[arg.index], &arg);
		} else if (BTREE_STATUS_RIGHT == arg.status) {
			dealBtreeStatusRight(str[arg.index], &arg);
		}
	}

	if (FALSE == arg.ok) {				// 要销毁生成了一半的二叉树中的节点！
		destroyBtree(arg.root);
		arg.root = NULL;
	}
	destoryStack(&arg.nodeStack);

	return arg.ok;
}

static int skipBlank(const char *str) {
	int index;

	for (index = 0; str[index] && isspace(str[index]); index++) {
		;
	}

	return index;
}

这里对上面函数的放置和声明做一些解释，因为我们提供的函数只是.h文件中那5个，剩下我们编写的函数都是为了辅助那5个函数编写而编写的，并且我们不希望那些函数被用户使用，所以我们将那些函数的声明放在了.c文件中，并且在那些函数的声明以及编写时在前面加上static修饰，表示仅在该文件中能够被使用。

作为数据结构与算法的最后几篇博文，希望能在这个时候让大家明白我们所编写的工具函数所在的.以及.h文件该怎样规划。

那么，工具函数文件我们都已经准备妥当了，现在来编写一个.c文件来调用这些工具函数来展示下使用方法吧：
demoBtree.c：

#include <stdio.h>

#include "mec.h"
#include "mecError.h"
#include "btree.h"

int main() {
	BTREE *root = NULL;
	char str[80];
	boolean ok;

	printf("请输入二叉树字符串:");
	gets(str);

	ok = createBTreeByString(str, &root);
	if (FALSE == ok) {
		showError();

		return -1;
	}
	printf("先根序遍历结果:
");
	travelFirstRoot(root);
	printf("
中根序遍历结果:
");
	travelMiddleRoot(root);
	printf("
后根序遍历结果:
");
	travelLastRoot(root);
	printf("
");

	destroyBtree(root);
	root = NULL;					//完全用完的指针赋值为NULL是一个好习惯，这点在今后的学习中会体现到

	return 0;
}

这次的代码还是需要通过命令行窗口或者虚拟机进行多文件联编，才能实现。
而且这次的代码与以往勾连过深，希望观看或者学习本篇博文的同学能够耐下性子先观看本人《堆栈的实现》以及《表达式的处理》两篇博文

《堆栈的实现》
《表达式的处理》

那么，这一节的知识就到此为止了，希望同学们对于二叉树的理解能更深一步。