题意
题目描述
在数轴上有 (N) 个闭区间 ([l_1,r_1],[l_2,r_2],...,[l_n,r_n]) 。现在要从中选出 (M) 个区间,使得这 (M) 个区间共同包含至少一个位置。换句话说,就是使得存在一个 (x) ,使得对于每一个被选中的区间 ([l_i,r_i]) ,都有 (l_i leq x leq r_i) 。
对于一个合法的选取方案,它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 ([l_i,r_i]) 的长度定义为 (r_i-l_i) ,即等于它的右端点的值减去左端点的值。
求所有合法方案中最小的花费。如果不存在合法的方案,输出 (-1) 。
输入输出格式
输入格式:
第一行包含两个正整数 (N,M) 用空格隔开,意义如上文所述。保证 (1 leq M leq N)
接下来 (N) 行,每行表示一个区间,包含用空格隔开的两个整数 (l_i) 和 (r_i) 为该区间的左右端点。
(N leq 500000,M leq 200000,0 leq l_i leq r_i leq 10^9)
输出格式:
只有一行,包含一个正整数,即最小花费。
输入输出样例
输入样例:
6 3
3 5
1 2
3 4
2 2
1 5
1 4
输出样例:
2
说明
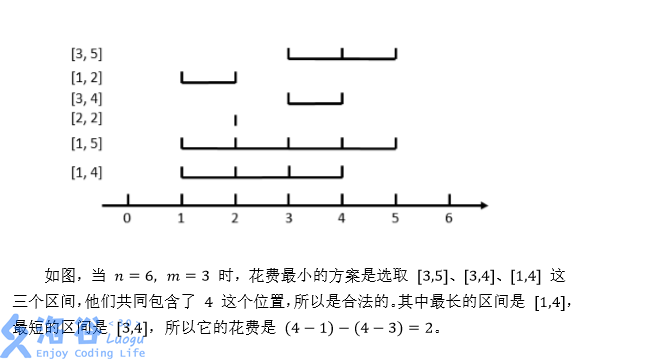
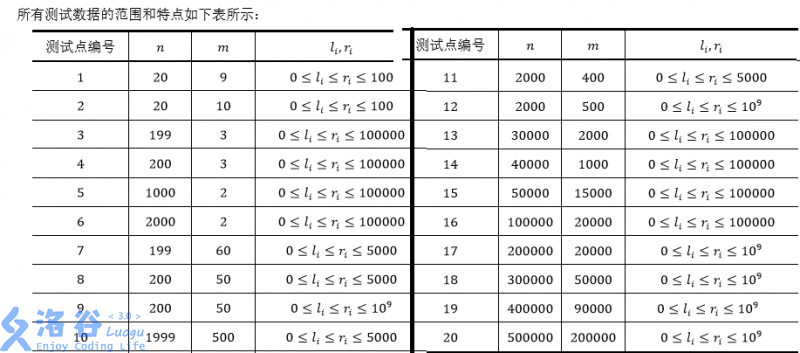
思路
2018-10-6 非完美算法测试唯一的可做题,然后用 (STL) 瞎搞了一波,只有 (60) 分 (qwq) 。赛后学习了 logeadd 的代码,就 (A) 掉了。
首先按照区间长度排序,然后我们枚举排序后的 ([1,M]) 的一段区间 ([L,R]) ,使得这一段区间能够刚好覆盖住同一个点 (m) 次,那么就可以用 (len[R]-len[L]) 来更新答案。
枚举区间可以使用尺取法,而判断这一区间是否合法可以用线段树。对于每一个区间 ([l_i,r_i]) ,我们在线段树上进行这个区间的区间加,然后统计区间最大值,就可以了。当然,这个数据范围是需要离散化的。
AC代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MAXN=5e5+5;
LL n,m,cnt,head,tail,ans=LLONG_MAX,s[MAXN],t[MAXN],num[MAXN<<1];
struct Segment
{
LL l,r,len;
bool operator < (const Segment &sjf) const {return len<sjf.len;}
}seg[MAXN];
struct SegmentTree
{
LL l,r,data,tag;
#define l(a) tree[a].l
#define r(a) tree[a].r
#define d(a) tree[a].data
#define t(a) tree[a].tag
}tree[MAXN<<3];
LL read()
{
LL re=0;
char ch=getchar();
while(!isdigit(ch)) ch=getchar();
while(isdigit(ch)) re=(re<<3)+(re<<1)+ch-'0',ch=getchar();
return re;
}
void build(LL p,LL ll,LL rr)
{
l(p)=ll,r(p)=rr;
if(ll==rr) return ;
LL mid=(ll+rr)>>1;
build(p<<1,ll,mid);
build(p<<1|1,mid+1,rr);
}
void pushdown(LL p)
{
if(t(p))
{
d(p<<1)+=t(p),d(p<<1|1)+=t(p);
t(p<<1)+=t(p),t(p<<1|1)+=t(p);
t(p)=0;
}
}
void change(LL p,LL ll,LL rr,LL k)
{
if(ll<=l(p)&&r(p)<=rr)
{
t(p)+=k,d(p)+=k;
return ;
}
pushdown(p);
LL mid=(l(p)+r(p))>>1;
if(mid>=ll) change(p<<1,ll,rr,k);
if(mid<rr) change(p<<1|1,ll,rr,k);
d(p)=max(d(p<<1),d(p<<1|1));
}
int main()
{
n=read(),m=read();
for(LL i=1;i<=n;i++) num[cnt++]=seg[i].l=read(),num[cnt++]=seg[i].r=read(),seg[i].len=seg[i].r-seg[i].l;
sort(seg+1,seg+n+1);
sort(num,num+cnt);
cnt=unique(num,num+cnt)-num;
for(LL i=1;i<=n;i++) seg[i].l=lower_bound(num,num+cnt,seg[i].l)-num,seg[i].r=lower_bound(num,num+cnt,seg[i].r)-num;
build(1,0,cnt-1);
while(1)
{
while(d(1)<m&&tail<n)
{
tail++;
change(1,seg[tail].l,seg[tail].r,1);
}
if(d(1)<m) break;
while(d(1)>=m&&head<n)
{
head++;
change(1,seg[head].l,seg[head].r,-1);
}
ans=min(ans,seg[tail].len-seg[head].len);
}
printf("%lld",ans==LLONG_MAX?-1:ans);
return 0;
}