一、题目
小易去附近的商店买苹果,奸诈的商贩使用了捆绑交易,只提供6个每袋和8个每袋的包装(包装不可拆分)。 可是小易现在只想购买恰好n个苹果,小易想购买尽量少的袋数方便携带。如果不能购买恰好n个苹果,小易将不会购买。
输入描述:
输入一个整数n,表示小易想购买n(1 ≤ n ≤ 100)个苹果
输出描述:
输出一个整数表示最少需要购买的袋数,如果不能买恰好n个苹果则输出-1
输入例子:
20
输出例子:
3
二、答案解析
此题用动态规划的思想就可以解决,题目要求出购买n个苹果的袋数最少的方案,容易理解,当n越来越大时,那么确定方案的难度就越大,因此,我们可以先规划出n较小时的最优方案,然后随着n的变大,不断修改方案,直到得出最终方案, 详细说一下解题的步骤:
1.首先创建一个长度为n+1的动态规划数组,数组元素i表示购买i个苹果的最少袋数dp[i];
2.对动态规划数组进行初始化,dp[0]的初始值当然是0了,然后将其他的元素初始化为Integer.MAX_VALUE,表示不可达,即不能恰好购买指定数量的苹果;
3.对动态规划数组进行遍历,我们详细描述一下遍历至元素i时的操作,首先判断当前元素的值是否为Integer.MAX_VALUE,若是则跳过当前循环,否则计算dp[i+6.的数值,在dp[i+6]的原始值和dp[i]+1(表示买一袋)中取最小值然后赋给dp[i+1],保证方案为最优方案,同样,我们需要进行dp[i+8]的计算,选出最优方案(注意:不过在进行计算是,一定要保证i+6或者i+8小于等于n,防止数组越界)
7.当循环结束时,判断dp[n]等于Integer.MAX_VALUE,那么输出-1.表示不能恰好购买n个苹果,否则输出dp[n],即为最优方案.
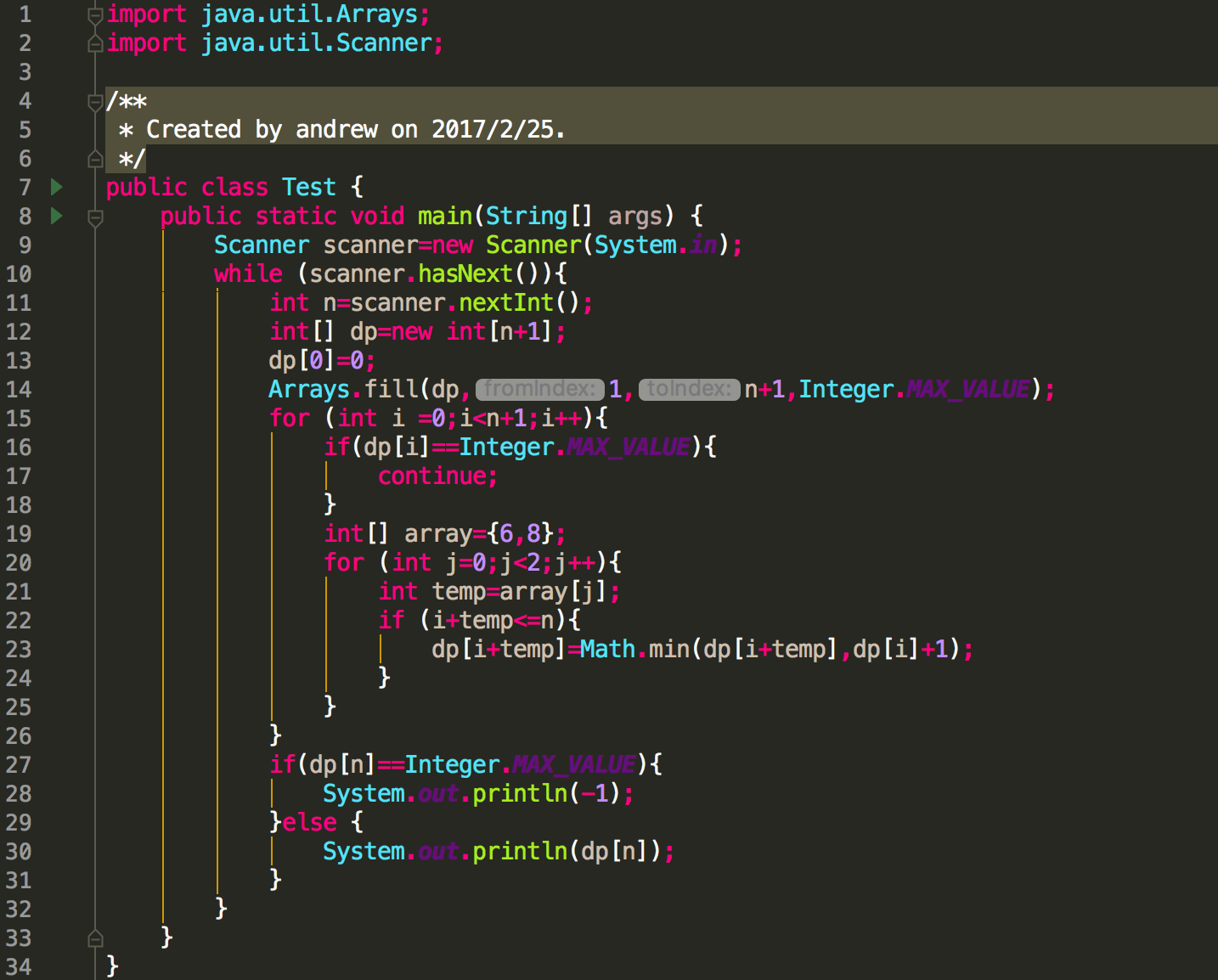
算法如下:
