公号:码农充电站pro
主页:https://codeshellme.github.io
在数据分析领域有一个经典的故事,叫做“尿布与啤酒”。
据说,在美国西部的一家连锁超市发现,很多男人会在周四购买尿布和啤酒。这样超市就可以将尿布与啤酒放在一起卖,便可以增加销售量。
“尿布与啤酒”这个案例就属于数据分析中的关联分析,也就是分析数据集中的内在隐含关系。
关联分析可以被用于发掘商品与商品之间的内在关联关系,进而通过商品捆绑销售或者相互推荐,来增加商品销量。
关联分析除了可以用于零售行业外,还可以用于网站流量分析和医药行业等。
Apriori 算法是一种发掘事物内在关联关系的算法,它可以加快关联分析的速度,从而让我们更有效的进行关联分析。
1,关联分析
关联分析用于发掘大规模数据集中的内在关系。
关联分析一般要分析数据集中的频繁项集(frequent item sets)和关联规则(association rules):
- 频繁项集:是数据集中频繁项的集合,集合中可以有一项或多项物品。
- 关联规则:暗示了两种物品之间可能存在很强的内在关系。
假设,我们收集了一家商店的交易清单:
| 交易编号 | 购物清单 |
|---|---|
| 1 | 牛奶,面包 |
| 2 | 牛奶,面包,火腿 |
| 3 | 面包,火腿,可乐 |
| 4 | 火腿,可乐,方便面 |
| 5 | 面包,火腿,可乐,方便面 |
频繁项集是一些经常出现在一起的物品集合。比如:{牛奶,面包},{火腿,方便面,可乐}都是频繁项集的例子。
项集中的物品,一般不考虑顺序关系。
关联规则意味着有人买了一种物品,还会买另一种物品。比如方便面->火腿,就是一种关联规则,表示如果买了方便面,还会买火腿。
2,三个重要概念
关联分析中有三个重要的概念,分别是:
- 支持度
- 可信度 / 置信度
- 提升度
支持度
要进行关联分析,首先要寻找频繁项,也就是频繁出现的物品集。那么怎样才叫频繁呢?我们可以用支持度来衡量频繁。
支持度是针对项集来说的,一个项集的支持度就是该项集的记录占总记录的比例。通常可以定义一个最小支持度,从而只保留满足最小支持度的项集。
一个项集{A} 的支持度的定义如下:
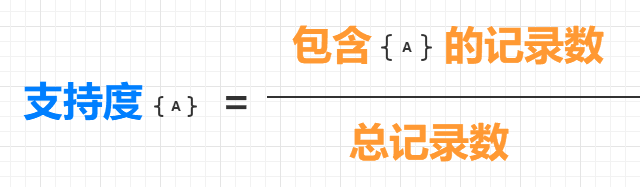
比如,在上面表格中的5 项记录中,{牛奶} 出现在了两条记录中,所以{牛奶} 的支持度为 2/5;而{面包,火腿} 出现在了三条记录中,所以{面包,火腿}的支持度为3/5。
可信度
可信度又叫置信度,它是针对关联规则来说的,比如{火腿}->{可乐}。
一个关联规则{A}->{B} 表示,如果购买了物品A,会有多大的概率购买物品B?它的可信度的定义如下:
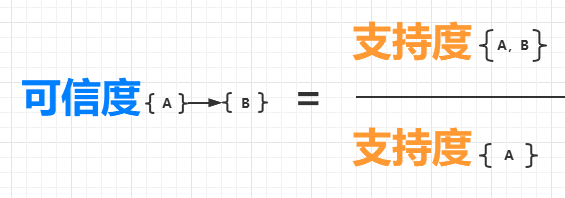
所以,在上面的表格中,{火腿,可乐} 的支持度是 3/5,{火腿} 的支持度是 4/5,所以{可乐}->{火腿} 的可信度为 3/5 除以 4/5,等于 0.75。这意味着,如果购买了火腿,有 75% 的可能性会购买可乐。
提升度
提升度也是针对关联规则来说的,它表示的是“如果购买物品A,会对购买物品B 的概率提升多少”。
一个关联规则{A}->{B} 的提升度的定义如下:

提升度会有三种情况:
- 提升度{A}->{B} > 1:表示购买物品A 对购买物品B 的概率有提升。
- 提升度{A}->{B} = 1:表示购买物品A 对购买物品B 的概率没有提升,也没有下降。
- 提升度{A}->{B} < 1:表示购买物品A 对购买物品B 的概率有下降。
3,如何寻找频繁项
寻找频繁项的一个简单粗暴的方法是,对所有的物品进行排列组合,然后计算所有组合的支持度,这种算法也可以叫做穷举法。
穷举法
穷举法就是列出所有物品的组合,然后计算每种组合的支持度。
比如,我们有一个物品集{0,1,2,3},其中有四个物品,那么所有的物品组合如下:
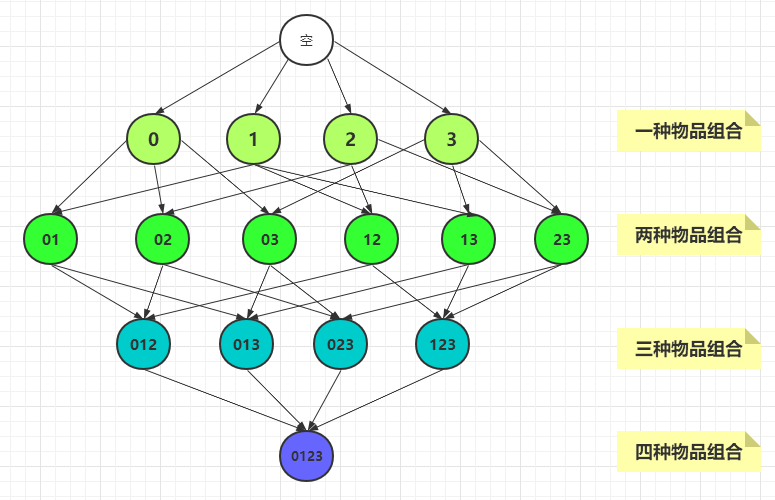
从图中可以看到一共有15 种组合,计算每一种组合的支持度都需要遍历一遍所有的记录,检查每个记录中是否包含该组合。因此有多少种组合,就需要遍历多少遍记录,时间复杂度则会很大。
可以总结出:包含N 种物品的数据集,共有 2N - 1 种组合。为了计算每种组合的支持度,则需要遍历 2N - 1 次记录。
如果一个商店中有100 款商品,将会有1.26*1030 种组合,这是一个非常庞大的数字。而普通商店一般都会有成千上万的商品,那么组合数将大到无法计算。
4,Apriori 算法
为了降低计算所需的时间,1994 年 Agrawal 提出了著名的 Apriori 算法,该算法可以有效减少需要计算的组合的数量,避免组合数量的指数增长,从而在合理的时间内计算出频繁项集。
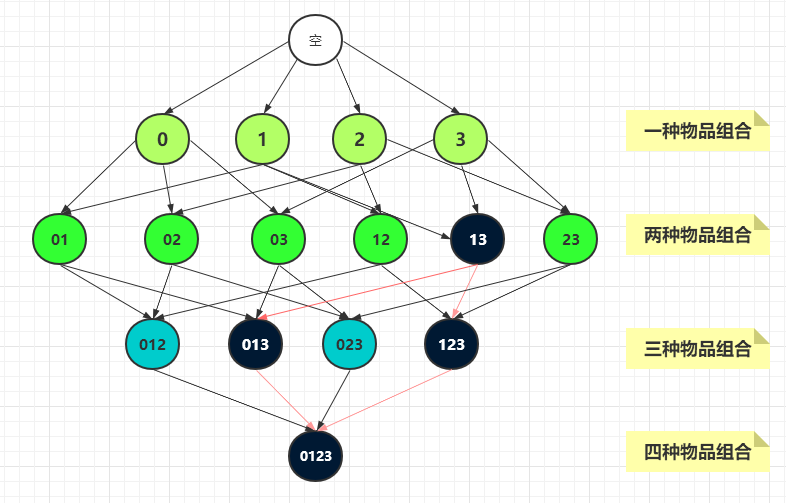
Apriori 原理是说:如果一个项集是非频繁集,那么它的所有超集也是非频繁的。
比如下图中的项集{1,3} 是非频繁集,那么{0,1,3},{1,2,3},{0,1,2,3} 就都是非频繁项集。这就大大减少了需要计算的项集的数量。
5,Apriori 算法的实现
这里,我们使用Apriori 算法来寻找上文表格中的购物清单的频繁项集(为了方便查看,我把表格放在这里)。
| 交易编号 | 购物清单 |
|---|---|
| 1 | 牛奶,面包 |
| 2 | 牛奶,面包,火腿 |
| 3 | 面包,火腿,可乐 |
| 4 | 火腿,可乐,方便面 |
| 5 | 面包,火腿,可乐,方便面 |
efficient_apriori 模块
Efficient-Apriori 包是Apriori 算法的稳定高效的实现,该模块适用于 Python 3.6+。
使用Apriori 算法要先安装:
pip install efficient-apriori
efficient_apriori 包中有一个 apriori 函数,原型如下(这里只列出了常用参数):
apriori(data,
min_support = 0.5,
min_confidence = 0.5)
参数的含义:
- data:表示数据集,是一个列表。列表中的元素可以是元组,也可以是列表。
- min_support:表示最小支持度,小于最小支持度的项集将被舍去。
- 该参数的取值范围是 [0, 1],表示一个百分比,比如0.3 表示30%,那么支持度小于30% 的项集将被舍去。
- 该参数的默认值为0.5,常见的取值有0.5,0.1,0.05。
- min_confidence:表示最小可信度。
- 该参数的取值范围也是 [0, 1]。
- 该参数的默认值为0.5,常见的取值有1.0,0.9,0.8。
使用 apriori 函数
首先,将表格中的购物清单转化成 Python 列表,如下:
data = [
('牛奶', '面包'),
('牛奶', '面包', '火腿'),
('面包', '火腿', '可乐'),
('火腿', '可乐', '方便面'),
('面包', '火腿', '可乐', '方便面')
]
挖掘频繁项集和频繁规则:
# 该函数的使用很简单,就一行代码
# 最小支持度为 0.5
# 最小可信度为 1
itemsets, rules = apriori(data, min_support=0.5, min_confidence=1)
查看频繁项集和频繁规则:
>>> itemsets # 频繁项集
{1: { # 只有一个元素的项集
('面包',): 4, # 4 表示记录数
('火腿',): 4,
('可乐',): 3
},
2: { # 有两个元素的项集
('火腿', '面包'): 3,
('可乐', '火腿'): 3
}
}
>>> rules # 频繁规则
[{可乐} -> {火腿}]
6,总结
本篇文章主要介绍了什么是关联分析,关联分析中三个重要的概念,以及 Apriori 算法。
Apriori 算法用于加快关联分析的速度,但它也需要多次扫描数据集。其实除了Apriori 算法,还有其它算法也可以加快寻找频繁项集的速度。
2000 年提出的FP-Growth 算法,对 Apriori 算法进行了改进。FP-Growth 通过创建一棵 FP树来存储频繁项集。对不满足最小支持度的项不会创建节点,减少了存储空间。而且整个生成过程只遍历数据集 2 次,大大减少了计算量。
另外,还有CBA 算法,GSP 算法等,都对Apriori算法进行了改进,这里不再详细介绍。
(本节完。)
推荐阅读:
欢迎关注作者公众号,获取更多技术干货。
