题目描述
在 W 星球上有 n 个国家。为了各自国家的经济发展,他们决定在各个国家 之间建设双向道路使得国家之间连通。但是每个国家的国王都很吝啬,他们只愿 意修建恰好 n – 1 条双向道路。 每条道路的修建都要付出一定的费用,这个费用等于道路长度乘以道路两端 的国家
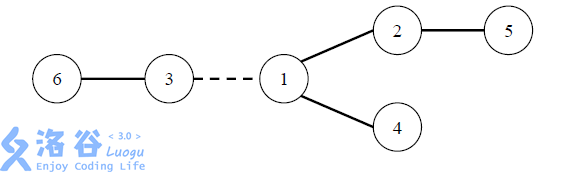
个数之差的绝对值。例如,在下图中,虚线所示道路两端分别有 2 个、4 个国家,如果该道路长度为 1,则费用为 1×|2 – 4|=2。图中圆圈里的数字表示国 家的编号。
由于国家的数量十分庞大,道路的建造方案有很多种,同时每种方案的修建 费用难以用人工计算,国王们决定找人设计一个软件,对于给定的建造方案,计 算出所需要的费用。请你帮助国王们设计一个这样的软件。
输入输出格式
输入格式:
输入的第一行包含一个整数 n,表示 W 星球上的国家的数量,国家从 1 到 n 编号。 接下来 n – 1 行描述道路建设情况,其中第 i 行包含三个整数 ai、bi和 ci,表 示第 i 条双向道路修建在 ai与 bi两个国家之间,长度为 ci。
输出格式:
输出一个整数,表示修建所有道路所需要的总费用。
每个边的实际花费费用为道路的权乘以道路两端的国家个数之差的绝对值,那么如果我们预处理每个点的子树的大小siz
通过树的遍历来遍历每一条边,因为是从我们求siz时使用的根出发,那么对于u->v的一条边,v的那一头的国家数量就是siz[v],而u的那一头的国家数量就是n-siz[v]
我们将两个数相减取绝对值abs(siz[v]-n+siz[v]),再乘以边权,就是每个边的实际花费费用
注意:不开long long 似乎要WA
总体实现如下:
#include <algorithm> #include <iostream> #include <cmath> #include <cstring> #include <map> #include <string> #include <vector> #include <queue> #include <stack> #include <cstdio> #include <cstdlib> using namespace std; inline int read() { register int p(1),a(0);register char ch=getchar(); while((ch<'0'||ch>'9')&&ch!='-') ch=getchar(); if(ch=='-') p=-1,ch=getchar(); while(ch>='0'&&ch<='9') a=a*10+ch-48,ch=getchar(); return a*p; } const int N=1000100; int n,u,v,w,siz[N],head[N],cnt=0; long long ans=0; struct EDGE{int nxt,val,to;}e[N<<1]; void add(int u,int v,int w){e[++cnt]=(EDGE){head[u],w,v};head[u]=cnt;} void dfs(int u,int fa) { siz[u]=1; for(int i=head[u],v=e[i].to;i;i=e[i].nxt,v=e[i].to) if(fa!=v) { dfs(v,u); siz[u]+=siz[v]; } } void dfs2(int u,int fa) { for(int i=head[u],v=e[i].to;i;i=e[i].nxt,v=e[i].to) if(fa!=v) { ans+=(abs(siz[v]-n+siz[v])*1ll*e[i].val); dfs2(v,u); } } int main() { // freopen("input","r",stdin); // freopen("output","w",stdout); n=read(); for(int i=1;i<n;i++) { u=read(),v=read(),w=read(); add(u,v,w);add(v,u,w); } dfs(1,-1); dfs2(1,-1); printf("%lld",ans); return 0; }