二叉堆(Heap)

　　其实在我学习二叉堆之前,我一直使用优先队列来实现堆完成堆优的Dijkstra,和其他操作,但此次我学习平衡树treap的时候,要用到堆的思想,所以我不得不学习一下二叉堆

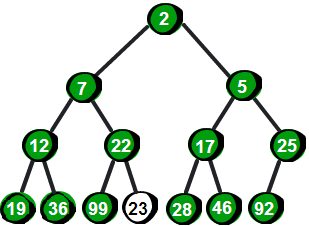
　　一个二叉堆(以下均简称为堆),首先是一棵完全二叉树,满足树高近似于logn,这就能够保证其复杂度在logn级别,以下我们拿小根堆举例

1. 小根堆的性质: 

　　一个合格的堆需要满足每一个结点都大于等于其父节点,这样我们才能保证,堆顶是最小的值

2. 堆的加入操作

堆的加入操作相当简单,只需要将节点数目tot加1,再将data[tot]赋为我们要加入的权值,

但这样做,不一定满足堆的性质,这时候,我们就要找他的父节点,而他的父节点是data[多少]呢?

我们记起我们之前有提到过,堆是一个完全二叉树,那么我们可以利用线段树对树形的处理方法,及每一个节点的两个子节点编号分别为该节点的编号乘2和乘2加1,

那么我们要满足小根堆的性质,就是要满足data[o]<=data[o<<1]&&data[o]<=data[o<<1|1]

,回到我们刚才的问题,于是我们便可以想到除了根节点每个节点的父节点编号为为其编号除以2,我们将新加入的点与其父节点进行比较,如果不满足堆性质就交换两点,

换后如果还是不满足性质便向上交换到满足位置

　　　　　　　　　　　　　　　　　　　　　　　　　　

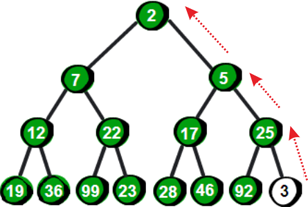
　　我们在第二层的时候发现已经满足条件,就停止调整操作

　　　　　　　　　　　　　　　　　　　　　　　　　　

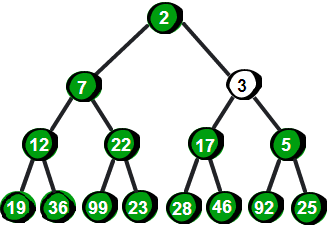
实现如下:

void insert(int x)
{
    data[++tot]=x;
    int temp=tot;
    while(temp!=1&&data[temp>>1]>data[temp]) swap(data[temp],data[temp>>1]),temp>>=1;
}

3. 堆的删除堆顶操作

删除操作,一开始我是自己yy的一个写法(或者说利用了平衡树的删除思想)

我将堆顶元素赋值为0x3f3f3f3f,将其与其左右儿子节点比较,把权值较小的儿子节点与该节点交换位置,就这样换换不已,一直把它换到堆底,

实现如下:

void del()
{
    /*-------slow-delete-------*/
    int temp=1;
    while((temp<<1|1)<=tot)
    {
        if(data[temp<<1]>data[temp<<1|1]) swap(data[temp],data[temp<<1|1]),temp=temp<<1|1;
        else swap(data[temp],data[temp<<1]),temp<<=1;
    }
    if((temp<<1)<=tot) swap(data[temp],data[temp<<1]),temp<<=1;
    data[temp]=0x3f3f3f3f;
}

这种方法显会更耗时间和空间,我们有一个更好的方法(其实和我的也差不多)

我们把data[tot],及最后一个节点与堆顶交换权值,再将tot--,这样就相当于删去了堆顶元素,再用我刚才说的方法去换换不已,一直把它换到它满足堆的性质为止

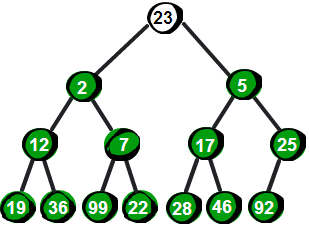
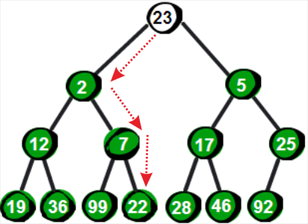
实现如下:

void del()
{
    swap(data[tot--],data[1]);
    int temp=1;
    while((temp<<1|1)<=tot&&min(data[temp<<1],data[temp<<1|1])<data[temp])
    {
        if(data[temp<<1]>data[temp<<1|1]) swap(data[temp],data[temp<<1|1]),temp=temp<<1|1;
        else swap(data[temp],data[temp<<1]),temp<<=1;
    }
    if((temp<<1)<=tot&&data[temp<<1]<data[temp]) swap(data[temp],data[temp<<1]),temp<<=1;
}

完整代码如下

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <map>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>
#include <set>
using namespace std;
inline int read()
{
    int a=0,p=0;char ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
    if(ch=='-') p=1,ch=getchar();
    while(ch>='0'&&ch<='9') a=a*10+ch-48,ch=getchar();
    return p?-a:a;
}
const int N=1000010;
int tot=0,data[N],t,op,x;
void insert(int x)
{
    data[++tot]=x;
    int temp=tot;
    while(temp!=1&&data[temp>>1]>data[temp]) swap(data[temp],data[temp>>1]),temp>>=1;
}
// void del()
// {
//     /*-------slow-delete-------*/
//     int temp=1;
//     while((temp<<1|1)<=tot)
//     {
//         if(data[temp<<1]>data[temp<<1|1]) swap(data[temp],data[temp<<1|1]),temp=temp<<1|1;
//         else swap(data[temp],data[temp<<1]),temp<<=1;
//     }
//     if((temp<<1)<=tot) swap(data[temp],data[temp<<1]),temp<<=1;
//     data[temp]=0x3f3f3f3f;
// }
void del()
{
    swap(data[tot--],data[1]);
    int temp=1;
    while((temp<<1|1)<=tot&&min(data[temp<<1],data[temp<<1|1])<data[temp])
    {
        if(data[temp<<1]>data[temp<<1|1]) swap(data[temp],data[temp<<1|1]),temp=temp<<1|1;
        else swap(data[temp],data[temp<<1]),temp<<=1;
    }
    if((temp<<1)<=tot&&data[temp<<1]<data[temp]) swap(data[temp],data[temp<<1]),temp<<=1;
}
int main()
{
    // freopen("data","r",stdin);
    // freopen("out","w",stdout);
    t=read();
    while(t--)
    {
        op=read();
        if(op==1) insert(read());
        else if(op==2) printf("%d
",data[1]);
        else if(op==3) del();
    }
    return 0;
}

 图片来源于网络,如有侵权请联线修改