线段树

　　线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

对于线段树中的每一个非叶子节点[o],若其表示的区间为[l,r]，它的左儿子表示的区间为[l,mid]，右儿子表示的区间为[mid+1,r]。因此线段树是平衡二叉树，最后的子节点数目为n，即整个线段区间的长度。

　　使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logn）。而未优化的空间复杂度为4n，因此有时需要离散化让空间压缩。

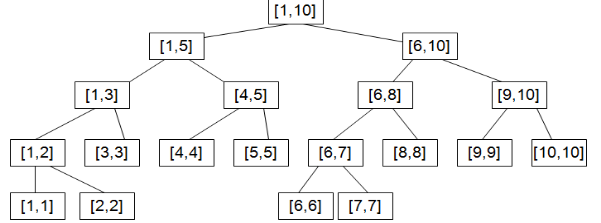
　　线段树可以支持的操作可分为两种：单点修改和区间修改

建树操作（单点修改与区间修改通用）

void build(int l,int r,int o)
{
    if(l==r){scanf("%d",&sum[o]);return;}
    int mid=(l+r)>>1;
    build(lson);
    build(rson);
    sum[o]=sum[o<<1]+sum[o<<1|1];
}

单点修改，区间查询：

int update(int pre,int val,int l,int r,int o)
{
    if(l==r) {sum[o]+=val;return;}
    int mid=(l+r)>>1;
    if(pre<=mid) update(pre,val,lson);
    else update(pre,val,rson);
    sum[o]=sum[o<<1]+sum[o<<1|1]
}
int query(int L,int R,int l,int r,int o)
{
    if(L<=l&&r<=R) return sum[o];
    int mid=(l+r)>>1;
    int ans=0;
    if(L<=mid) ans+=query(L,R,lson);
    if(R> mid) ans+=query(L,R,rson);
    return ans;
}

　　在区间修改的时候，如果我们一个一个点的去修改那么复杂度将会变得很高，这时候我们就要用到一个叫懒标记(lazy tag)的东西，若整个区间都要修改，就将该区间改变后的值算出来，给它打上一个标记，若日后要查询区间中的一段，或修改区间中的一段再将其展开

void pushdown(int lnum,int rnum,int o)
{
    if(lazy[o])
    {
        sum[o<<1]+=lnum*lazy[o];
        sum[o<<1|1]+=rnum*lazy[o];
        lazy[o<<1]+=lazy[o];
        lazy[o<<1|1]+=lazy[o];
        lazy[o]=0;
    }
}
void update(int L,int R,int v,int l,int r,int o)//添加 
{
    if(L<=l&&r<=R) {lazy[o]+=v;sum[o]+=v*(r-l+1);return;}
    int mid=(l+r)>>1;
    pushdown(mid-l+1,r-mid,o);
    if(L<=mid) update(L,R,v,lson);//左 
    if(R> mid) update(L,R,v,rson);//右 
    sum[o]=sum[o<<1]+sum[o<<1|1];//更新
}
int query(int L,int R,int l,int r,int o)//查询 
{
    if(L<=l&&r<=R) return sum[o];
    int mid=(l+r)>>1,ans=0;
    pushdown(mid-l+1,r-mid,o);
    if(L<=mid) ans+=query(L,R,lson);//左 
    if(R> mid) ans+=query(L,R,rson);//右 
    return ans;
}