【ybtoj】【倍增问题】图上查询

题意

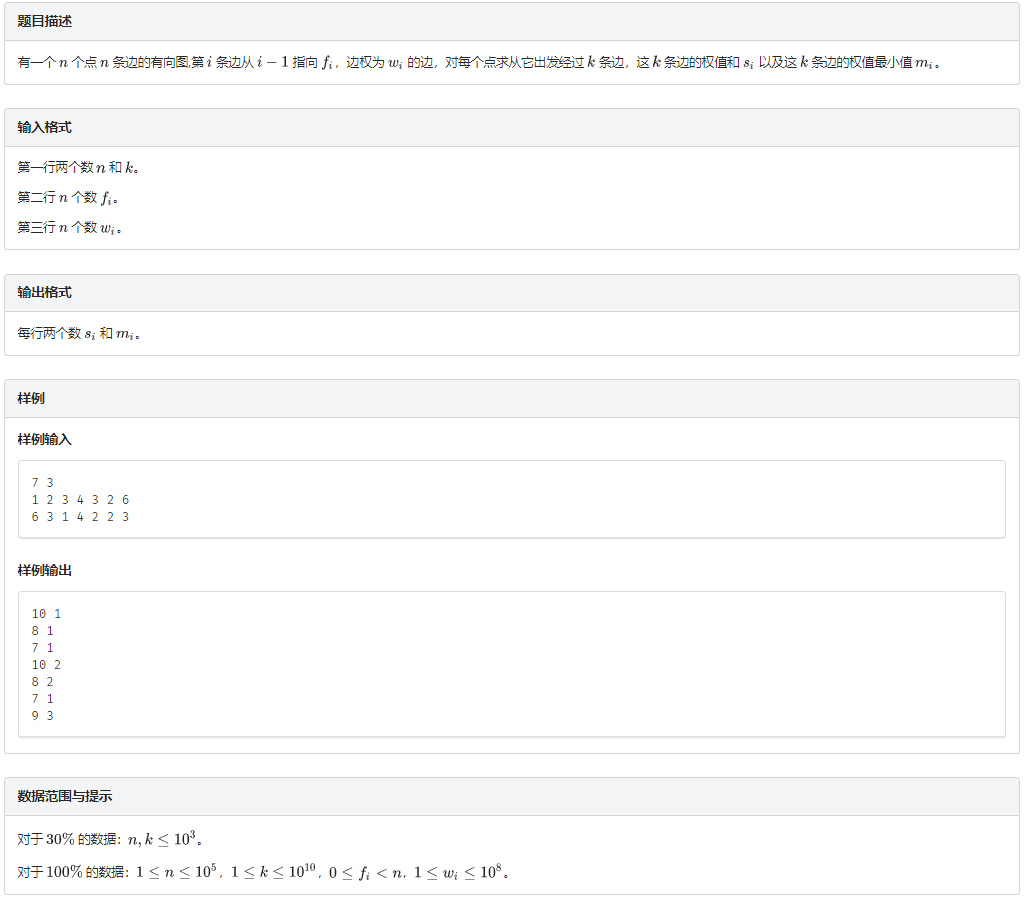
题解

可以很好地巩固倍增基础...(水题)
设计(sum[i][j],dis[i][j])表示从(i)开始走了(2^j)步路径上的权值和/最小权值，初始值(sum[i][0]=dis[i][0]=w[i])，转移过程和倍增的转移几乎完全一样
注意一下点是(0 hicksim n-1)

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 1e5+10;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
ll k;
int n,to[N][36],w[N];
ll s[N],m[N],sum[N][36],dis[N][36];
int main()
{
	n=read(),k=read();
	for(int i=1;i<=n;i++) to[i-1][0]=read(),m[i-1]=1e18;
	for(int i=1;i<=n;i++) 
		w[i]=read(),dis[i-1][0]=sum[i-1][0]=w[i];
	for(int i=1;i<=34;i++)
		for(int j=0;j<n;j++) 
		{
			to[j][i]=to[to[j][i-1]][i-1];
			dis[j][i]=min(dis[to[j][i-1]][i-1],dis[j][i-1]);
			sum[j][i]=sum[j][i-1]+sum[to[j][i-1]][i-1];
		
		}
	for(int j=0;j<n;j++) 	
	{
		ll now=j,cnt=k;
		for(int i=34;i>=0;i--)
		{
			if((1ll<<i)<=cnt) 
			{
				s[j]+=sum[now][i],
				m[j]=min(m[j],dis[now][i]),
				now=to[now][i],cnt-=1ll<<i;
				//printf("dis=%lld,sum=%lld,to=%d
",dis[j][i],sum[j][i],to[j][i]);
			}
		}
	}
	for(int i=0;i<n;i++) 
		printf("%lld %lld
",s[i],m[i]);
	return 0;
}