1、二叉树的遍历
是指从二叉树的根结点出发,按照某种次序依次访问二叉树中的所有结点,使得每个结点被访问一次,且仅被访问一次。
二叉树的访问次序可以分为四种:
前序遍历
中序遍历
后序遍历
层序遍历
1.1、前序遍历通俗的说就是从二叉树的根结点出发,当第一次到达结点时就输出结点数据,按照先向左在向右的方向访问。
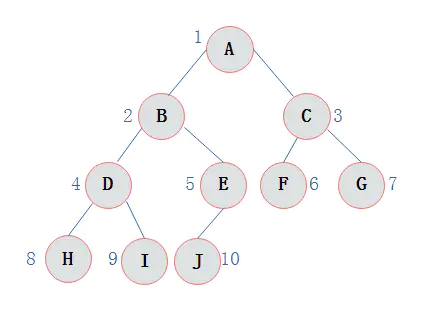
上图所示二叉树访问如下:
从根结点出发,则第一次到达结点A,故输出A; 继续向左访问,第一次访问结点B,故输出B; 按照同样规则,输出D,输出H; 当到达叶子结点H,返回到D,此时已经是第二次到达D,故不在输出D,进而向D右子树访问,D右子树不为空,则访问至I,第一次到达I,则输出I; I为叶子结点,则返回到D,D左右子树已经访问完毕,则返回到B,进而到B右子树,第一次到达E,故输出E; 向E左子树,故输出J; 按照同样的访问规则,继续输出C、F、G; 作者:MrHorse1992 链接:https://www.jianshu.com/p/bf73c8d50dc2 来源:简书 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
则上图所示二叉树的前序遍历输出为: ABDHIEJCFG
1.2、中序遍历就是从二叉树的根结点出发,当第二次到达结点时就输出结点数据,按照先向左在向右的方向访问。
上图所示二叉树中序访问如下:
从根结点出发,则第一次到达结点A,不输出A,继续向左访问,第一次访问结点B,不输出B;继续到达D,H;
到达H,H左子树为空,则返回到H,此时第二次访问H,故输出H;
H右子树为空,则返回至D,此时第二次到达D,故输出D;
由D返回至B,第二次到达B,故输出B;
按照同样规则继续访问,输出J、E、A、F、C、G;
则上图所示二叉树的中序遍历输出为:HDIBJEAFCG
1.3、后序遍历就是从二叉树的根结点出发,当第三次到达结点时就输出结点数据,按照先向左在向右的方向访问。
上图所示二叉树后序访问如下:
从根结点出发,则第一次到达结点A,不输出A,继续向左访问,第一次访问结点B,不输出B;继续到达D,H;
到达H,H左子树为空,则返回到H,此时第二次访问H,不输出H;
H右子树为空,则返回至H,此时第三次到达H,故输出H;
由H返回至D,第二次到达D,不输出D;
继续访问至I,I左右子树均为空,故第三次访问I时,输出I;
返回至D,此时第三次到达D,故输出D;
按照同样规则继续访问,输出J、E、B、F、G、C,A;
则上图所示二叉树的后序遍历输出为:HIDJEBFGCA
当然前中后三种遍历方式,也可以简单的理解为:
前序就是 父节点->左子树->右子树,
中序是 左子树->父节点->右子树,
后序是 左子树 -> 右子树 ->父节点
递归在其中非常重要,每棵子树又可以重新遍历,依此类推,遍历完成。
1.4、层次遍历
层次遍历就是按照树的层次自上而下的遍历二叉树。针对上图所示二叉树的层次遍历结果为:ABCDEFGHIJ
2、二叉树重建
二叉树的重建,只能在提供前序+中序,或者后序+中序的情况下,才可以正常的重构。
- 前序+中序:
1、前序遍历数组中的第一个数就是根节点,得到根节点的数字。
2、然后在中序遍历中找到该根节点的位置,中序数组的左边就是该根节点的左子树,中序遍历的右边序列是其右子树。
3、前序遍历中根据中序遍历中根节点的位置,将前序遍历分为前序遍历的左子树和右子树。
4、根节点就确定了,最后将前序和中序划分出来的左右子树,分别带入递归得到左右子树的构建情况。 - 后序+中序
1.后续遍历的最后一个节点是根节点,然后中序遍历中找出根节点位置mid。
2.再在根据中序遍历中的mid位置将后序遍历数组和中序遍历数据分为左子树和右子树。
3.最后将划分完成的左右子树递归。
Java代码实现如下:
public class RebuildBinaryTree { //假设输入的前序遍历和中序遍历的结果中都不含重复的数字 /* 前序遍历第一位是根节点; 中序遍历中,根节点左边的是根节点的左子树,右边是根节点的右子树。 例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}。 首先,根节点 是{ 1 }; 左子树是:前序{ 2,4,7 } ,中序{ 4,7,2 }; 右子树是:前序{ 3,5,6,8 } ,中序{ 5,3,8,6 }; 这时,如果我们把左子树和右子树分别作为新的二叉树,则可以求出其根节点,左子树和右子树。 */
/*
pre 前序序列数组
in 中序序列数组
*/
public TreeNode reConstructBinaryTree(int [] pre,int [] in) { if(pre==null||in==null){ return null; } TreeNode treeNode=reConstructBinaryTree(pre, in,0,pre.length-1,0,in.length-1); return treeNode; }
/*
pre 前序序列数组
in 中序序列数组
preStart 前序序列第一个节点的索引值
preEnd 前序序列最后一个节点的索引值
inStart 中序序列第一个节点的索引值
inEnd 中序序列最后一个节点的索引值
*/
public TreeNode reConstructBinaryTree(int [] pre,int [] in,int preStart,int preEnd,int inStart,int inEnd) { TreeNode tree=new TreeNode(pre[preStart]); //前序遍历的第一个是根节点,递归时把左子树和右子树分别作为新的二叉树 tree.left=null; tree.right=null; if(preStart==preEnd&&inStart==inEnd){ //说明已经是树叶节点 return tree; } int root; for(root=inStart;root<inEnd;root++){ //寻找根节点在中序遍历中的下标 if(pre[preStart]==in[root]){ break; } } int leftLength=root-inStart; //左子树的长度 int rightLength=inEnd-root; //右子树的长度 //把左子树和右子树分别作为新的二叉树,则可以求出其根节点,左子树和右子树。 if(leftLength>0){ tree.left=reConstructBinaryTree(pre,in,preStart+1,preStart+leftLength,inStart,root-1); } if(rightLength>0){ tree.right=reConstructBinaryTree(pre,in,preStart+1+leftLength,preEnd,root+1,inEnd); } return tree; } }