目录
- 常用标记
- logistic回归
- 梯度下降法
- 计算图
- 向量化
一、常用标记
样本:$(x, y)$ $x$为输入,$y$为输出
输入$x$:$xinmathbb{R}^{n_{x}}$是一个$n_{x}$维的特征向量
输出$y$:取值为0或1
样本数量:$m$
样本空间:${(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})}$
如何组织:按列来组织,每一列表示一个样本
矩阵$X=[x^{(1)},x^{(1)},...,x^{(m)}]$
矩阵$Y=[y^{(1)},y^{(1)},...,y^{(m)}]$
sigmoid函数:$g(z) = frac{1}{(1 + e^{-z})} $ $z$的范围为正负无穷,$g(z)$结果范围为$[0,1]$
二、logistic回归
- 逻辑回归
逻辑回归是监督学习中用来解决输出为0/1问题的算法。通过sigmoid将线性结果映射到(0,1)空间,作为概率估计。它的目标是最小化预测与训练结果间的误差
- 实例
例:Cat vs No - cat
给定以特征向量$x$表示的一张图,算法会评估出猫在该图中的概率

具体步骤
1. 输入样本数据$x$
2. $z = w^Tx + b = w_1x_1 + w_2x_2...+w_nx_n + b$,不能直接表达分类结果
3. sigmoid函数(激活函数),输出结果$widehat{y}=sigma (z)$。把z转换成(0,1)之间的数,就是对$p(y=1|x)$的概率估计
4. 规定if$ y = 1: p(y|x) = widehat{y}$,则 if$ y = 0: p(y|x) = 1 - widehat{y}$
把上述式子合并,$p(y|x) = widehat y^y(1-widehat y)^{(1-y)}$
5. 目标:输出结果与标签相近,也就是$widehat y approx y$
6. 评估误差——loss函数(单个样本)
$l(widehat y, y)=-log(y|x)=-(ylog widehat y + (1-y)log (1-widehat y))$
- 为什么不用$|widehat y - y|^2$?
目标(最优化问题):找出一组参数,使得$J(w,b)$取到最小值
求解的思想:最大似然概率:http://blog.csdn.net/zengxiantao1994/article/details/72787849
$l(w,b)=l(widehat y, y)=|widehat y - y|^2$,$l(w)$不是一个凸函数,也就是有多个极小值。若用梯度下降法来求解,不一定能得到最小值
$l(w,b)=l(widehat y, y)=-log(y|x)$,$l(w)$一个凸函数,也就是只有一个最小值,利用梯度下降是可以收敛到最小的位置
7. 评估误差——cost函数(m个样本独立同分布)
$log p(整个样本空间标签)=log prod p(y^{(i)}|x^{(i)}) = sum log p(y^{(i)}|x^{(i)}) = -sum l(widehat{y}^{(i)},y^{(i)})$
cost函数:$J(w,b)=sum l(widehat{y}^{(i)},y^{(i)})$
三、梯度下降法
利用梯度下降法来学习模型中的参数$w$和$b$,使得cost函数取到是小值
梯度:函数在某一点方向导数最大的向量,函数在该点变化最快
梯度下降法:从某个点开始,每次朝最陡(梯度)的方向移动,最后可以到达全局最优(或相近位置)
为什么用梯度下降法:cost中的参数较多,如果用最大似然概率估计法,需要对各参数求偏导,计算量较大
为什么可以用梯度下降法:cost函数是一个凸函数($frac{f(x_1)+f(x_2)}{2}geq frac{f(x_1+x_2)}{2}$)
实现:对$w$求偏导以更新$w$:$w:=w-alpha frac{ dJ(w,b)}{dw}$ $alpha$是学习率;b的更新方法与w相似
四、计算图
把一个计算式分成多个步骤写成一个流程图,前向传导是一步步计算,而后向传导则可以帮助求导
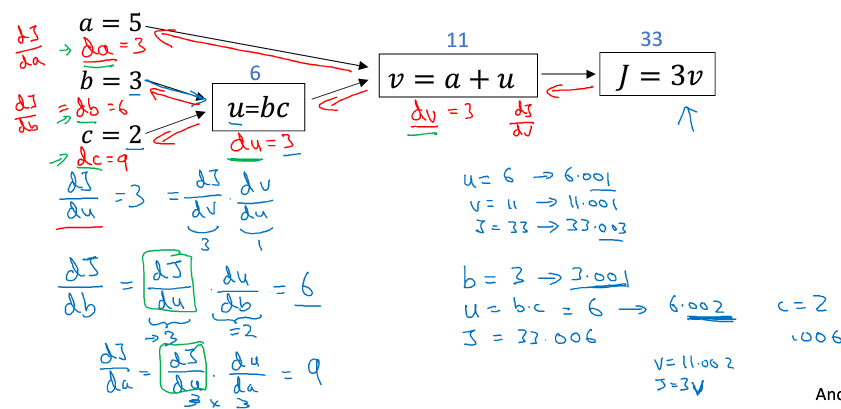
五、向量化
把for的显示循环用向量的方式计算,调用一些内置的函数,可以充分利用并行的优势以加快速度;能尽量少用for循环则少用
例
|
$z^{(1)}=w^Tx^{(1)}+b$;$a^{(1)}=sigma (z^{(1)})$ $z^{(2)}=w^Tx^{(2)}+b$;$a^{(2)}=sigma (z^{(2)})$ $z^{(3)}=w^Tx^{(3)}+b$;$a^{(3)}=sigma (z^{(3)})$ 向量化: $X=[x^{(1)} x^{(2)} x^{(3)}...]$ $Z=[z^{(1)} z^{(2)} z^{(3)}...]=w^TX+b$ $A=[a^{(1)} a^{(2)} a^{(3)}...]=sigma(Z)$ |
python中的广播:一个向量和另一个向量(或一个实数)运算,则其中维数较少的向量或实数会自动扩展成与另一个向量维数相同的向量,并进行元素上的运算
避免因为广播导致bug的方法:
- 不使用秩为1的向量(不是行向量也不是列向量),而使用行、列都是确定的向量
- assert(a.shape==(5,1)) 来断言一个向量的维度
- 使用一个不确定维数的向量时使用reshape