Bresenham算法

2.1.2 Bresenham算法

　

    Bresenham算法是计算机图形学典型的直线光栅化算法。

本文转自上交大计算机图形学网

• 从另一个角度看直线光栅化显示算法的原理
  • 由直线的斜率确定选择在x方向或y方向上每次递增（减）1个单位，另一变量的递增（减）量为0或1，它取决于实际直线与最近光栅网格点的距离，这个距离的最大误差为0.5。

  　

• 1)Bresenham的基本原理

  　

  • 假定直线斜率k在0~1之间。此时，只需考虑x方向每次递增1个单位，决定y方向每次递增0或1。

    设

        直线当前点为(xi,y)
        直线当前光栅点为(xi,yi)

    则

        下一个直线的点应为(xi+1,y+k)
        下一个直线的光栅点
            或为右光栅点(xi+1,yi)（y方向递增量0）
            或为右上光栅点(xi+1,yi+1)（y方向递增量1）

       

    

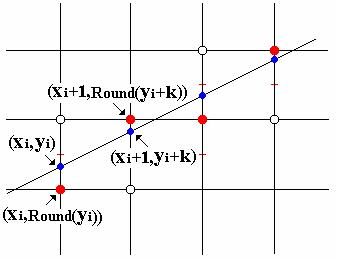    记直线与它垂直方向最近的下光栅点的误差为d，有：d=(y+k)–yi，且

        0≤d≤1
        当d<0.5：下一个象素应取右光栅点(xi+1,yi)
        当d≥0.5：下一个象素应取右上光栅点(xi+1,yi+1)

    

    

    如果直线的（起）端点在整数点上，误差项d的初值：d0＝0，
    x坐标每增加1，d的值相应递增直线的斜率值k，即：d＝d + k。
    一旦d≥1，就把它减去1，保证d的相对性，且在0-1之间。

    令e=d-0.5，关于d的判别式和初值可简化成：

        e的初值e0= -0.5，增量亦为k;
        e<0时，取当前象素(xi,yi)的右方象素(xi+1,yi)；
        e>0时，取当前象素(xi,yi)的右上方象素(xi+1,yi+1)；
        e=0时，可任取上、下光栅点显示。

    Bresenham算法的构思巧妙：它引入动态误差e，当x方向每次递增1个单位，可根据e的符号决定y方向每次递增 0 或 1。

        e<0，y方向不递增
        e>0，y方向递增1
        x方向每次递增1个单位，e = e + k

    因为e是相对量，所以当e>0时，表明e的计值将进入下一个参考点（上升一个光栅点），此时须：e = e - 1

    　

• 2)Bresenham算法的实施——Rogers 版

  　

  • 通过(0,0)的所求直线的斜率大于0.5，它与x=1直线的交点离y=1直线较近，离y=0直线较远，因此取光栅点(1,1)比(1,0)更逼近直线；
    如果斜率小于0.5，则反之；
    当斜率等于0.5，没有确定的选择标准，但本算法选择(1,1)

    

    

    （程序）

    　

    • //Bresenham’s line resterization algorithm for the first octal.
      //The line end points are (xs,ys) and (xe,ye) assumed not equal.
      // Round is the integer function.
      // x,y, ∆x, ∆y are the integer, Error is the real.
      //initialize variables
      x=xs
      y=ys
      ∆x = xe -xs
      ∆y = ye -ys
      //initialize e to compensate for a nonzero intercept
      Error =∆y/∆x-0.5
      //begin the main loop
      for i=1 to ∆x
          WritePixel (x, y, value)
          if (Error ≥0) then
              y=y+1
              Error = Error -1
          end if
          x=x+1
          Error = Error +∆y/∆x
      next i
      finish

    　

• 3)整数Bresenham算法

  　

  • 上述Bresenham算法在计算直线斜率和误差项时要用到浮点运算和除法，采用整数算术运算和避免除法可以加快算法的速度。

    由于上述Bresenham算法中只用到误差项（初值Error =∆y/∆x-0.5）的符号

    因此只需作如下的简单变换：

        NError = 2*Error*∆x

    即可得到整数算法，这使本算法便于硬件（固件）实现。

    （程序）

    　

    • //Bresenham’s integer line resterization algorithm for the first octal.
      //The line end points are (xs,ys) and (xe,ye) assumed not equal. All variables are assumed integer.
      //initialize variables
      x=xs
      y=ys
      ∆x = xe -xs
      ∆y = ye -ys
      //initialize e to compensate for a nonzero intercept
      NError =2*∆y-∆x                 //Error =∆y/∆x-0.5
      //begin the main loop
      for i=1 to ∆x
          WritePixel (x, y)
          if (NError >=0) then
              y=y+1
              NError = NError –2*∆x  //Error = Error -1
          end if
          x=x+1
          NError = NError +2*∆y       //Error = Error +∆y/∆x
      next i
      finish

    　

• 4)一般Bresenham算法

  　

  • 要使第一个八卦的Bresenham算法适用于一般直线，只需对以下2点作出改造：
    当直线的斜率|k|>1时，改成y的增量总是1，再用Bresenham误差判别式确定x变量是否需要增加1；
    x或y的增量可能是“+1”或“-1”，视直线所在的象限决定。

    （程序）

    　

    • //Bresenham’s integer line resterization algorithm for all quadrnts
      //The line end points are (xs,ys) and (xe,ye) assumed not equal. All variables are assumed integer.
      //initialize variables
      x=xs
      y=ys
      ∆x = abs(xe -xs)        //∆x = xe -xs
      ∆y = abs(ye -ys)        //∆y = ye -ys
      sx = isign(xe -xs)
      sy = isign(ye -ys)
      //Swap ∆x and ∆y depending on the slope of the line.
      if ∆y>∆x then
          Swap(∆x,∆y)
          Flag=1
      else
          Flag=0
      end if
      //initialize the error term to compensate for a nonezero intercept
      NError =2*∆y-∆x
      //begin the main loop
      for i=1 to ∆x
          WritePixel(x, y , value)
          if (Nerror>=0) then
              if (Flag) then     //∆y>∆x，Y=Y+1
                  x=x+sx
              else
                  y=y+sy
              end if             // End of Flag
              NError = NError –2*∆x
          end if                 // End of Nerror
           if (Flag) then        //∆y>∆x，X=X+1
              y=y+sy
          else
              x=x+sx
          end if
          NError = NError +2*∆y
      next i
      finish

    　

• 例子

  •