时间序列分解
大量时间序列的观测样本表现出趋势性、季节性和随机性,或者三者中的其一或其二。于是,我们认为每个时间序列,都可以分为三个部分的叠加
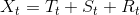
其中,T是趋势项,S是季节项,R是随机项。
上述公式表现了趋势项和季节项是累加的,实际应用场景中,趋势项和季节项可能是累乘的,时间序列可以分解为如下公式
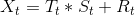
实际应用中,随机项R的期望为0,没有规律,并且绝对值不大。所以在应用场景中我们往往省略掉R,R称作噪声。预测公式如下
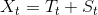
或
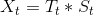
一次指数平滑法
线性回归算法中,每个经验点的权重是一致的,即很早以前的经验数据也可能对预测数据有较大的影响。很多实际场景中,未来一段时间的趋势可能和在最近一段时间的趋势关系更加紧密。比如小明去年数学考试成绩一直不及格,今年连续多次考试90多分,预测小明下一次数学考试的成绩,情理上90多分的可能性更高。采用传统的线性回归算法,预测结果可能是70多分。
指数平滑法认为越老的经验数据对趋势的影响越小。我们假定时间t的观测值为y(t),时间t的预测值为S(t),则时间t+1的预测值S(t+1)为
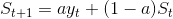
a的取值范围(0, 1),a越大,最近时间点的观测值对预测值的影响越大。
假设我们有t个经验数据,根据上述一次指数平滑公式,预测值S(t + n) = S(t + 1),预测值不具备趋势。
二次指数平滑
我们对一次指数平滑值再进行指数平滑,可以获得趋势。二次指数平滑法的预测模型为:
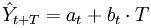
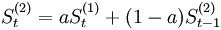
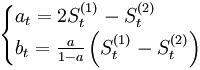
式中: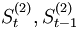 分别为时间t和时间t - 1的二次指数平滑值。
分别为时间t和时间t - 1的二次指数平滑值。
三次指数平滑
二次指数模型是线性的,对于非线性趋势预测我们可以使用三次指数平滑法。公式如下
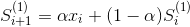
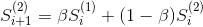
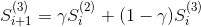
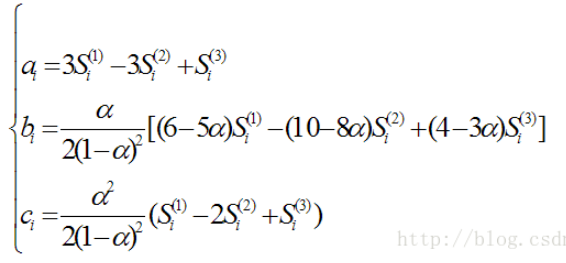
![]()
Holt-Winters算法
对于具有周期性的趋势预测,我们可以使用Holt-Winters算法。累乘性Holt-Winters公式如下

其中,alpha,beta,gamma取值范围为(0, 1),分别表示全局因子,趋势因子,周期性因子中最近时间点数据对预测数据的影响程度。y为经验数据,L为周期。
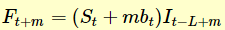 表示使用t时间点的估计值预测t+m时间点的值。
表示使用t时间点的估计值预测t+m时间点的值。
注:预测公式中I(t – L + m)应该为I(t – L + 1 + (m – 1) mod L)
计算步骤
alpha,beta,gamma,y,L,m已知。
(1)初始化S0
S0 = y0
(2)初始化b0
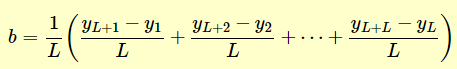
(3)初始化I1, I2, …, IL

(3)计算所有S,b,I
(4)根据公式预测未来值。其中,t取经验数据最后一个时间点,t+m为预测时间点。
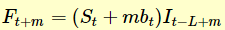
累加性Holt-Winters公式
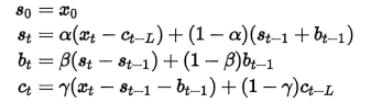
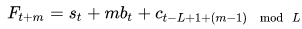
Holt-Winters理解
指数平滑法与Holt-Winters不是建立在理论基础上的,而是一种经验法则。文章开发我们讨论了时间序列的分解,Holt-Winters公式正是把时间序列分解为趋势项和周期项。其中趋势项为线性函数s + mb,周期项为c。这里面趋势项与周期项考虑了指数平滑,即给不同时间点的趋势或者周期性赋予了不同的权重。不过,这里的趋势仅仅是线性趋势,在带有季节性的非线性趋势预测中,效果可能不那么好。
Holt-Winters的Java实现
下面的代码实在google上搜索的,预测公式逻辑有问题,没有对季节项进行mod运算,会导致数组越界,有空再修改代码。
package coshaho.learn; public class HoltWinters { public static double[] forecast(int[] y, double alpha, double beta, double gamma, int period, int m, boolean debug) { if (y == null) { return null; } int seasons = y.length / period; double a0 = calculateInitialLevel(y, period); double b0 = calculateInitialTrend(y, period); double[] initialSeasonalIndices = calculateSeasonalIndices(y, period, seasons); if (debug) { System.out.println(String.format( "Total observations: %d, Seasons %d, Periods %d", y.length, seasons, period)); System.out.println("Initial level value a0: " + a0); System.out.println("Initial trend value b0: " + b0); printArray("Seasonal Indices: ", initialSeasonalIndices); } double[] forecast = calculateHoltWinters(y, a0, b0, alpha, beta, gamma, initialSeasonalIndices, period, m, debug); if (debug) { printArray("Forecast", forecast); } return forecast; } private static double[] calculateHoltWinters(int[] y, double a0, double b0, double alpha, double beta, double gamma, double[] initialSeasonalIndices, int period, int m, boolean debug) { double[] St = new double[y.length]; double[] Bt = new double[y.length]; double[] It = new double[y.length]; double[] Ft = new double[y.length + m]; //Initialize base values St[1] = a0; Bt[1] = b0; for (int i = 0; i < period; i++) { It[i] = initialSeasonalIndices[i]; } Ft[m] = (St[0] + (m * Bt[0])) * It[0];//This is actually 0 since Bt[0] = 0 Ft[m + 1] = (St[1] + (m * Bt[1])) * It[1];//Forecast starts from period + 2 //Start calculations for (int i = 2; i < y.length; i++) { //Calculate overall smoothing if((i - period) >= 0) { St[i] = alpha * y[i] / It[i - period] + (1.0 - alpha) * (St[i - 1] + Bt[i - 1]); } else { St[i] = alpha * y[i] + (1.0 - alpha) * (St[i - 1] + Bt[i - 1]); } //Calculate trend smoothing Bt[i] = gamma * (St[i] - St[i - 1]) + (1 - gamma) * Bt[i - 1]; //Calculate seasonal smoothing if((i - period) >= 0) { It[i] = beta * y[i] / St[i] + (1.0 - beta) * It[i - period]; } //Calculate forecast if( ((i + m) >= period) ){ Ft[i + m] = (St[i] + (m * Bt[i])) * It[i - period + m]; } if(debug){ System.out.println(String.format( "i = %d, y = %d, S = %f, Bt = %f, It = %f, F = %f", i, y[i], St[i], Bt[i], It[i], Ft[i])); } } return Ft; } /** * See: http://robjhyndman.com/researchtips/hw-initialization/ * 1st period's average can be taken. But y[0] works better. * * @return - Initial Level value i.e. St[1] */ private static double calculateInitialLevel(int[] y, int period) { /** double sum = 0; for (int i = 0; i < period; i++) { sum += y[i]; } return sum / period; **/ return y[0]; } /** * See: http://www.itl.nist.gov/div898/handbook/pmc/section4/pmc435.htm * * @return - Initial trend - Bt[1] */ private static double calculateInitialTrend(int[] y, int period){ double sum = 0; for (int i = 0; i < period; i++) { sum += (y[period + i] - y[i]); } return sum / (period * period); } /** * See: http://www.itl.nist.gov/div898/handbook/pmc/section4/pmc435.htm * * @return - Seasonal Indices. */ private static double[] calculateSeasonalIndices(int[] y, int period, int seasons){ double[] seasonalAverage = new double[seasons]; double[] seasonalIndices = new double[period]; double[] averagedObservations = new double[y.length]; for (int i = 0; i < seasons; i++) { for (int j = 0; j < period; j++) { seasonalAverage[i] += y[(i * period) + j]; } seasonalAverage[i] /= period; } for (int i = 0; i < seasons; i++) { for (int j = 0; j < period; j++) { averagedObservations[(i * period) + j] = y[(i * period) + j] / seasonalAverage[i]; } } for (int i = 0; i < period; i++) { for (int j = 0; j < seasons; j++) { seasonalIndices[i] += averagedObservations[(j * period) + i]; } seasonalIndices[i] /= seasons; } return seasonalIndices; } private static void printArray(String description, double[] data){ System.out.println(String.format("******************* %s *********************", description)); for (int i = 0; i < data.length; i++) { System.out.println(data[i]); } System.out.println(String.format("*****************************************************************", description)); } }