[USACO21FEB] Minimizing Edges P

题目

点这里看题目。

分析

这道题就离离离离离谱

首先不难发现 (f_G(u,x)) 实际上只和到达 (u) 的奇偶最短路长度相关。

那么很快就导出一种特例——即对于某个点，存在两种奇偶性的最短路的情况，可以发现此时 (G) 是二分图。那么我们只需要考虑一种最短路，因此可以直接建立最短路树，得到答案为 (n-1) 。

考虑一般情况，即 (G) 上面有奇环的情况，此时对于任意的点，都有两种奇偶性的最短路。因此可以设 (d_u) 表示 (u) 的最短路，而用 (d'_u) 表示 (u) 的奇偶性与 (d_u) 不同的另一条最短路。一个显然的性质是 (d<d') 。

分析一下 (G') 必须满足的条件：

1. 在 (u) 的邻接点中，必须有一个点 (v) ，满足 (d_u=d_v+1) ；
2. 在 (u) 的邻接点中，必须有一个点 (v) ，满足 (d'_u=d'_v+1) 或者 (d'_u=d_v+1) ；

注意到我们其实只关心 ((d,d')) 这样的有序对，我们就可以得到集合 (S(d,d')={u|d_u=d,d'_u=d'}) 。再简化一点，我们其实只关心 (S(d,d')) 的大小，所以我们可以直接设 (f(d,d')=|S(d,d')|) 。

根据之前的条件，我们再分析一下对于 ((d,d')) ，它的连边情况：

1. 直接和 ((d-1,d'-1)) 相连；
2. 直接和 ((d-1,d'+1)) 和 ((d+1,d'-1)) 相连；
3. 如果 (d+1=d') ，此时可以和 ((d-1,d'+1)) 和 ((d,d')) 相连，这种情况特殊在它的表现是在 (S) 内部连边；

画一个图会更好理解：

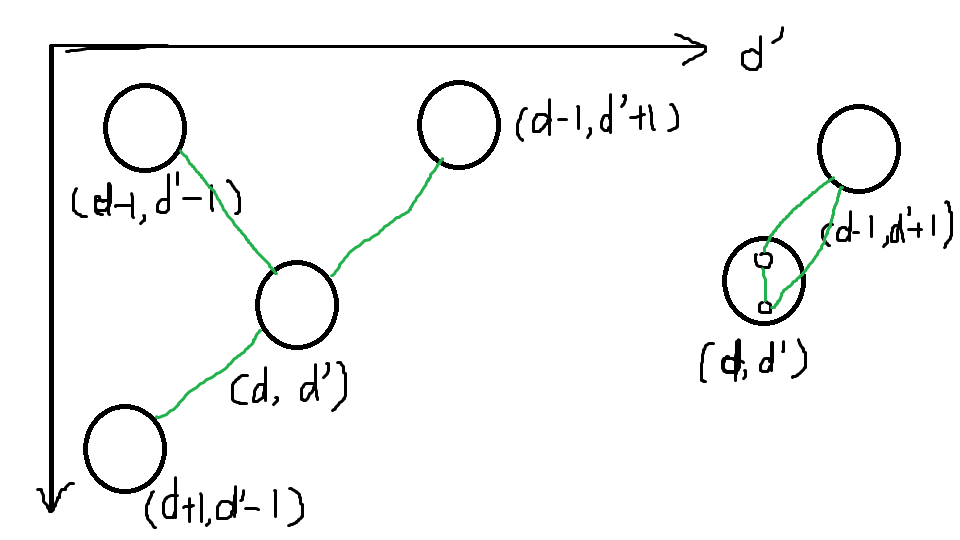
绿色为合法连边。上图左侧是一般的连边，上图右侧是内部的连边

注意到，如果按照 (d+d') 分层，那么只有 1 为跨层连，而 2,3 均为同层连。这启发我们可以按照 (d+d') 和 (d) 的优先级进行处理。

一个显然的性质是：如果我们可以找到一种最优的连边方法，使得每个点的 (d) 和 (d') 都可以转移过来，那么这就是最优解之一。

其实不一定很显然，但是看起来是对的，证明 " 下次一定 "

因此我们就可以考虑给每个点找相邻点，不难想到可以按顺序贪心！

下面我们就可以愉快地讨论了：

1. 如果 (f(d-1,d'-1)>0,f(d-1,d'+1)=0) ，那么没得说，只能全部连到 (f(d-1,d'-1)) 上；

2. 如果 (f(d-1,d'-1)>0,f(d-1,d'+1)>0) 且 (d+1<d') ，此时有可能 (S(d-1,d'+1)) 的点需要连接到 (S(d,d')) 中的点来。设这样的需求边为 (t) 条，分类讨论：

   1. 如果 (tle f(d,d')) ，那么可以先分配 (t) 个连接，剩下的点可以直接连到 ((d-1,d'-1)) 上面一次解决问题；而钦定的 (t) 个点还需要满足 (d') ，因此需要向 (S(d+1,d'-1)) 连 (t) 条边。
   2. 如果 (t>f(d,d')) ，那么我们也可以重复地连 (t) 条边，此时 (S(d,d')) 里的点还需要满足 (d') 。经过下面的分析，我们可以知道将 (f(d,d')) 条边连至 ((d+1,d'-1)) 会更优。

   注意到上面我们默认存在 ((d+1,d'-1)) ；如果不存在，那么下传的给 ((d+1,d'-1)) 的边只能连到 ((d-1,d'-1)) 。

3. 如果 (f(d-1,d'-1)>0,f(d-1,d'+1)>0) 且 (d+1=d') ，此时我们可以在 ((d,d')) 内部连边。这部分的讨论类似于 2 部分；但特殊的情况是，这样的 ((d,d')) 一定找不到对应的 ((d+1,d'-1)) ，所以原本下传的 (t) 条边需要内部消化，不难发现这样的贡献是 (lceilfrac t 2 ceil) 。

   在这里我们也可以解释为什么 2.2 中需要下传：无论这 (t) 条边连在哪里，它一定会带来贡献；但如果向下传递，它就有可能连接到 (d+1=d') 的点，使得只缺 (d') 的点变多。粗算一下，只缺 (d') 的点代价为 (frac{1}{2}) ，而 (d,d') 都缺的点代价为 (1) ，显然这样会划算一些。

运用 set 可以获得 (O(nlog_2n)) 的复杂度，足以通过本题。如果分层并用指针应该可以做到 (O(n)) 。

小结：

1. 本题一个妙处在于不区分 (d,d') 的实际奇偶，而只关心相对奇偶，一下子就让讨论方便了许多。相当于是简化信息，关注相对信息。
2. 另一个妙处在于分析 ((d,d')) 的连接情况，使得需要考虑的连边大大减少，简化了问题。
3. 最后一个点在于目标的转化，我们将目标转化到了一个等效的状态——即每个点的 (d,d') 都得到了满足，那么它就是合法的。虽然并不是很显然，但它告诉我们可以从目标入手反推。

代码

点我查看代码

#include <set>
#include <cstdio>
#include <utility>
#include <algorithm>
using namespace std;

#define rep( i, a, b ) for( int i = (a) ; i <= (b) ; i ++ )
#define per( i, a, b ) for( int i = (a) ; i >= (b) ; i -- )

typedef pair<int, int> Node;

const int INF = 0x3f3f3f3f;
const int MAXN = 1e5 + 5, MAXM = 2e5 + 5;

#define DX first
#define DY second

template<typename _T>
void read( _T &x )
{
	x = 0; char s = getchar(); int f = 1;
	while( s < '0' || '9' < s ) { f = 1; if( s == '-' ) f = -1; s = getchar(); }
	while( '0' <= s && s <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar(); }
	x *= f;
}

template<typename _T>
void write( _T x )
{
	if( x < 0 ) putchar( '-' ), x = - x;
	if( 9 < x ) write( x / 10 );
	putchar( x % 10 + '0' );
}

struct Edge
{
	int to, nxt;
}Graph[MAXM << 2];

set<Node> s;
Node seq[MAXN];

int dist[MAXN << 1];

int head[MAXN << 1];
int N, M, cnt;

bool Cmp( const Node &x, const Node &y )
{
	int tx = x.DX + x.DY, ty = y.DX + y.DY;
	return tx == ty ? x.DX < y.DX : tx < ty;
}

void Clean()
{
	cnt = 0, s.clear();
	rep( i, 1, N << 1 ) head[i] = 0;
}

void AddEdge( const int from, const int to )
{
	Graph[++ cnt].to = to, Graph[cnt].nxt = head[from];
	head[from] = cnt;
}

void AddE( const int from, const int to )
{
	AddEdge( from, to ), AddEdge( to, from );
}

void BFS()
{
	static int q[MAXN << 1], h, t;
	h = 1, t = 0; rep( i, 1, N << 1 ) q[i] = 0;
	rep( i, 1, N << 1 ) dist[i] = INF;
	dist[q[++ t] = 1] = 0;
	for( int u, v ; h <= t ; )
	{
		u = q[h ++];
		for( int i = head[u] ; i ; i = Graph[i].nxt )
			if( dist[v = Graph[i].to] > dist[u] + 1 )
				dist[q[++ t] = v] = dist[u] + 1;
	}
}

int main()
{
	int T;
	read( T );
	while( T -- )
	{
		read( N ), read( M ), Clean();
		rep( i, 1, M ) { int a, b; 
			read( a ), read( b ); 
			AddE( a, b + N ), AddE( a + N, b );
		}
		BFS(); bool flg = true;
		rep( i, 1, N )
		{
			if( dist[i] < dist[i + N] ) seq[i] = Node( dist[i], dist[i + N] );
			else seq[i] = Node( dist[i + N], dist[i] );
			if( seq[i].DY == INF ) flg = false;
		}
		if( flg == false ) { write( N - 1 ), putchar( '
' ); continue; }
		
		sort( seq + 1, seq + 1 + N, Cmp ); int ans = 0, t = 0;
		for( int i = 1, r ; i <= N ; i = r )
		{
			for( r = i ; r <= N && seq[r] == seq[i] ; r ++ );
			s.insert( seq[i] );
			Node lu = Node( seq[i].DX - 1, seq[i].DY - 1 );
			flg = s.find( lu ) != s.end();
			if( t <= r - i ) 
			{
				if( flg ) ans += ( i > 1 ) * ( r - i );
				else ans += ( i > 1 ) * ( r - i ), t = r - i;
			}
			else ans += ( i > 1 ) * t, t = r - i;
			if( r > N || seq[r] != Node( seq[i].DX + 1, seq[i].DY - 1 ) )
			{
				if( seq[i].DX + 1 != seq[i].DY ) ans += t;
				else ans += t + 1 >> 1; t = 0;
			}
		}
		write( ans ), putchar( '
' );
	}
	return 0;
}