hdu 1281 棋盘游戏（匈牙利（最大匹配+枚举））

http://acm.hdu.edu.cn/showproblem.php?pid=1281

Problem Description

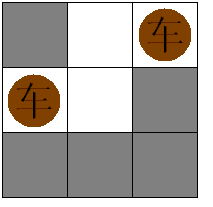
小希和Gardon在玩一个游戏：对一个N*M的棋盘，在格子里放尽量多的一些国际象棋里面的“车”，并且使得他们不能互相攻击，这当然很简单，但是Gardon限制了只有某些格子才可以放，小希还是很轻松的解决了这个问题（见下图）注意不能放车的地方不影响车的互相攻击。
所以现在Gardon想让小希来解决一个更难的问题，在保证尽量多的“车”的前提下，棋盘里有些格子是可以避开的，也就是说，不在这些格子上放车，也可以保证尽量多的“车”被放下。但是某些格子若不放子，就无法保证放尽量多的“车”，这样的格子被称做重要点。Gardon想让小希算出有多少个这样的重要点，你能解决这个问题么？

 

Input

输入包含多组数据，
第一行有三个数N、M、K(1<N,M<=100 1<K<=N*M)，表示了棋盘的高、宽，以及可以放“车”的格子数目。接下来的K行描述了所有格子的信息：每行两个数X和Y，表示了这个格子在棋盘中的位置。

 

Output

对输入的每组数据，按照如下格式输出：
Board T have C important blanks for L chessmen.

 

Sample Input

3 3 4 1 2 1 3 2 1 2 2 3 3 4 1 2 1 3 2 1 3 2

 

Sample Output

Board 1 have 0 important blanks for 2 chessmen. Board 2 have 3 important blanks for 3 chessmen.

 

 

怎么理解这题是最大匹配题呢？下面我们以第一组数据为例：

3 3 4

1 2

1 3

2 1

2 2

对于关系（1,2）跟（1,3），只能选择一个关系，因为他们两个在同一个x坐标下，这样的话就可以

理解为什么是最大匹配了吧！

这一层理解了就没什么难度了，直接套用模板

代码：

#include<iostream>
using namespace std;
int map[110][110],cx[110],mark[110],cy[110],m,n;
int path(int v)
{
    int i;
    for(i=1;i<=m;i++)
        if(map[v][i]&&!mark[i])
        {
            mark[i]=1;
            if(!cy[i]||path(cy[i]))
            {
                cx[v]=i;
                cy[i]=v;
                return 1;
            }
        }
    return 0;
}
int maxmatch()
{
    memset(cx,0,sizeof(cx));
    memset(cy,0,sizeof(cy));
    int i,sum=0;
    for(i=1;i<=n;i++)
        if(!cx[i])
        {
            memset(mark,0,sizeof(mark));
            sum+=path(i);
        }
    return sum;
}
int main()
{
    int t,a,b,k=1;
    while(~scanf("%d%d%d",&n,&m,&t))
    {
        memset(map,0,sizeof(map));
        while(t--)
        {
            scanf("%d%d",&a,&b);
            map[a][b]=1;
        }
        int ans=maxmatch();
        int i,j,count=0;
        for(i=1;i<=n;i++)
            for(j=1;j<=m;j++)
                if(map[i][j])
                {
                    map[i][j]=0;
                    if(ans!=maxmatch())
                        count++;
                    map[i][j]=1;
                }
        printf("Board %d have %d important blanks for %d chessmen.\n",k++,count,ans);
    }
    
    return 0;
}