Floyd算法是用来找出每对点之间的最短距离,对于图要求,可以是无向图也可以是有向图,边权可正可负,唯一要求就是不能有负环
Floyd算法基于动态规划的思想,以 u 到 v 的最短路径至少经过前 k 个点为转移状态进行计算,通过 k 的增加达到寻找最短路径的目的.当 k 增加 1 时,最短路径要么不边,如果改变,必经过第 k 各点,也就是说当起点 u 到第 k 个点的最短距离加上第 k 个点到终点 v 的最短路径小于不经过第 k 个节点的最优最短路经长度的时候更新 u 到 v 的最短距离. 当 k = n 时, u 到 v 的最短路径就确定了.
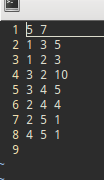 输入
输入
#include <bits/stdc++.h> using namespace std; typedef long long LL; const int INF = 0x3f3f3f3f; const int maxn = 10005; int maps[maxn][maxn];//存图 int dist[maxn][maxn];//存距离 int pre[maxn][maxn];//存i到j路径i的后一个结点 void Floyd(int n) { for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) { dist[i][j] = maps[i][j];//复制距离 pre[i][j] = j;//标记i的后一个结点 } for(int k = 1; k <= n; k++)//用k个点对每对顶点进行更新 for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) { if(dist[i][k] != INF && dist[k][j] != INF && dist[i][j] > dist[i][k] + dist[k][j]) { dist[i][j] = dist[i][k] + dist[k][j]; pre[i][j] = pre[i][k]; } } } void pfpath(int u, int v) { // 打印路径 while(u != v) { cout << u <<" "; u = pre[u][v]; } cout << u <<endl; } int main() { //freopen("in.txt","r",stdin); //freopen("out.txt","w",stdout); int n, m, u, v, w; while(cin >> n >> m) { for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) maps[i][j] = (i == j ? 0 : INF); for(int i = 1; i <= m; i++) { cin >> u >> v >> w; maps[v][u] = maps[u][v] = w; } Floyd(n); cout << dist[1][4] << endl; pfpath(1,4); } return 0; }