例27 回旋方阵
问题描述
编写程序,生成从内到外是连续的自然数排列的回旋方阵。例如,当n=3和n=4时的回旋方阵如下图1所示。

图1 由内到外回旋方阵
输入格式
一个正整数n(1≤n≤20)。
输出格式
N阶满足要求的由内到外回旋方阵。输出时共n行,每行n个数,每个数占4列。
输入样例
5
输出样例
21 20 19 18 17
22 7 6 5 16
23 8 1 4 15
24 9 2 3 14
25 10 11 12 13
(1)编程思路1。
观察图1及样例,由内到外回旋方阵的构造方法是:先将1填入方阵的中心位置(即i=(n-1)/2; j=(n-1)/2; a[i][j]=1),然后其余数的填写可以看成由向下填充(列号不变、行号加1,即i++)、向右填充(行号不变、列号加1,即j++)、向上填充(行号减1、列号不变,即i--)和向左填充(行号不变、列号减1,即j--)四个子过程不断交替完成的。
例如,图1所示的4阶由内到外回旋方阵可以看成由向下填充(2)、向右填充(3)、向上填充(4、5)、向左填充(6、7)、向下填充(8、9、10)、向右填充(11、12、13)、向上填充(14、15、16)这7个子过程完成的。
n阶由内到外回旋方阵可以看成由4个子过程交替进行来完成的,这4个子过程依次为向下填充、向右填充、向上填充、向左填充,用变量d来表示,其取值为1、2、3或4,1表示向下填充,2表示向右填充,3表示向上填充,4表示向左填充。每个子过程结束后,切换填充方向,方式为:d++,若d>4,d=1。
在这一序列子过程中,第1、2子过程填写1个数,第3、4子过程填写2个数,第5、6子过程填写3个数,第7、8子过程填写4个数,…,直到最后一个数n2填写完毕。
(2)源程序1。
#include<stdio.h>
int main()
{
int a[20][20]={0},i,j,k=1,n,x,d,cnt;
scanf("%d",&n);
i=(n-1)/2; j=(n-1)/2;
a[i][j]=k++;
d=1;cnt=1;x=0;
while (k<=n*n)
{
switch (d)
{
case 1:i++;
a[i][j]=k++;
x++;
if (x==cnt)
d=2,x=0;
break;
case 2:j++;
a[i][j]=k++;
x++;
if (x==cnt)
d=3,x=0,cnt++;
break;
case 3:i--;
a[i][j]=k++;
x++;
if (x==cnt)
d=4,x=0;
break;
case 4:j--;
a[i][j]=k++;
x++;
if (x==cnt)
d=1,x=0,cnt++;
break;
}
}
for (i=0;i<n;i++)
{
for (j=0;j<n;j++)
printf("%4d",a[i][j]);
printf(" ");
}
return 0;
}
(3)编程思路2。
观察1所示的由内到外回旋方阵,可以看出,n阶由内到外回旋方阵可以看成是自然数n*n~1由外向内递减填充数字而构造成。
构造时,奇数阶方阵从左下角开始(即row=n-1、col=0),循环经过向上填充、向右填充、向下填充和向左填充的过程,直到全部数字填充完毕;偶数阶方阵从右上角开始(即row=0、col=n-1),循环经过向下填充、向左填充、向上填充和向右填充的过程,直到全部数字填充完毕。由于奇数阶和偶数阶填充顺序有差异,定义一个变量s作为标志,s==1时,表示进行向下填充和向左填充;s==-1表示进行向上填充和向右填充。奇数阶构造时,s初值为-1;偶数阶时为1。
为了清楚地标记出每次填充结束的位置,定义x1、x2、y1和y2这四个变量来分别保存向上、向下、向左和向右填充的边界。初始时, x1=0、y1=0、x2=n、y2=n。
例如,向上填充时,循环过程为
while(row>=x1) // 向上填充
{
a[row][col]=num;
row--; // 行号减1、列号不变,向上填充
num--;
}
一次向上填充结束后,x1加1(即x1++),这样向上填充的上边界增大了,下次就会少填一行。 同时修改row和col,即row--、col--,从而得到向左填充的起点。
由于奇数阶方阵先向上填充,这样当向左填充时,最底行的左下角已经填有数字,因此,向左填充的边界的初始值应为1(即y1=1)。同理,偶数阶方阵的初始向右填充的边界y2=n-1。
(4)源程序2。
#include<stdio.h>
int main()
{
int row,col,a[20][20]={0},n,num;
int x1,x2,y1,y2,s;
// x1:填充上边界 x2:填充下边界
// y1:填充左边界 y2:填充右边界
// s:数组元素升降标记,s等于l为升,s等于-1为降
scanf("%d",&n);
num=n*n;
x1=0; y1=0; x2=n; y2=n;
if (n%2==0) { row=0;col=n-1; y2=n-1; s=1;}
else { row=n-1; col=0; y1=1; s=-1;}
while (num>=1)
{
if(s==1)
{
while (row<x2) // 向下填充
{ a[row][col]=num--;row++; }
row--; col--; // 得到向左填充的起点
x2--; // 向下填充的下边界缩小
while (col>=y1) // 向左填充
{ a[row][col]=num--;col--; }
col++; row--; // 得到向上填充的起点
y1++; // 向左填充的左边界增大
s=-1; // 切换升降标志
}
else
{
while(row>=x1) // 向上填充
{ a[row][col]=num--; row--; }
row++; col++; // 得到向右填充的起点
x1++; // 向上填充的上边界增大
while (col<y2) // 向右填充
{a[row][col]=num--;col++;}
col--; row++; // 得到向下填充的起点
y2--; // 向右填充的右边界缩小
s=1; // 切换升降标志
}
}
for (int i=0;i<n;i++)
{
for (int j=0;j<n;j++)
printf("%4d",a[i][j]);
printf(" ");
}
return 0;
}
习题27
27-1 由外向内回旋方阵
问题描述
编写程序,生成从外到内是连续的自然数排列的回旋方阵。例如,当n=3和n=4时的回旋方阵如下图2所示。
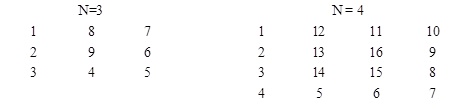
图2 由外向内回旋方阵
输入格式
一个正整数n(1≤n≤20)。
输出格式
N阶满足要求的由外向内回旋方阵。输出时共n行,每行n个数,每个数占4列。
输入样例
5
输出样例
1 16 15 14 13
2 17 24 23 12
3 18 25 22 11
4 19 20 21 10
5 6 7 8 9
(1)编程思路。
由外向内回旋方阵可以通过对方阵的每一圈的各边的各个元素顺序赋值来完成。每一圈的赋值又依次包含4个顺序的过程。
1)一圈的左列从上至下递增赋值,一直赋值到超过最底行(即row==n)或下一位置已经赋值了(即a[row+1][col]!=0)。
while(row+1<n && !a[row+1][col])
a[++row][col]=++num; // 列号col不变,行号row递增,数num递增
2)一圈的下行从左至右递增赋值,一直赋值到超过最右列(即col==n)或下一位置已经赋值了(即a[row][col+1]!=0)。
while(col+1<n&&!a[row][col+1])
a[row][++col]=++num; // 行号row不变,列号col递增,数num递增
3)一圈的右列从下至上递增赋值,一直赋值到超过最顶列(即row==-1)或下一位置已经赋值了(即a[row-1][col]!=0)。
while(row-1>=0&&!a[row-1][col])
a[--row][col]=++num; // 行号row递减,列号col不变,数num递增
4)一圈的上行从右至左递增赋值,一直赋值到超过最左列(即col==-1)或下一位置已经赋值了(即a[row][col-1]!=0)。
while(col-1>=0&&!a[row][col-1])
a[row][--col]=++num; // 行号row不变,列号col递减,数num递增
初始时,row=0、col=0、num=1。
(2)源程序。
#include<stdio.h>
int main()
{
int a[20][20]={0};
int n,row,col,num=0;
scanf("%d",&n);
num=a[row=0][col=0]=1; // 第0行第0列输入起始1
while(num<n*n) // 数组中的数不超过n*n
{
while(row+1<n && !a[row+1][col]) // 向下填充
a[++row][col]=++num;
while(col+1<n&&!a[row][col+1]) // 向右填充
a[row][++col]=++num;
while(row-1>=0&&!a[row-1][col]) // 向上填充
a[--row][col]=++num;
while(col-1>=0&&!a[row][col-1]) // 向左填充
a[row][--col]=++num;
}
for (int i=0;i<n;i++)
{
for (int j=0;j<n;j++)
printf("%4d",a[i][j]);
printf(" ");
}
return 0;
}
27-2 间断折叠方阵
问题描述
n阶间断折叠方阵是把从起始数1开始的n2个整数折叠为n行n列的n阶方阵:起始数1置于方阵的左上角,然后从起始数开始递增,每一层从第1行开始,先竖向下再折转向左,层层折叠地排列为间断折叠方阵。
例如,当n=4和n=5时的间断折叠方阵如下图3所示。

图3 间断折叠方阵
输入格式
一个正整数n(1≤n≤20)。
输出格式
N阶满足要求的间断折叠方阵。输出时共n行,每行n个数,每个数占4列。
输入样例
5
输出样例
1 2 5 10 17
4 3 6 11 18
9 8 7 12 19
16 15 14 13 20
25 24 23 22 21
(1)编程思路。
定义一个二维数组a保存方阵的各元素,从给定的起始数1开始,按递增1取值,根据间断折叠方阵的构造特点给二维数组a[n][n]赋值。
起始数1赋值给a[0][0]。
除a[0][0]外,n阶方阵还有叠折的n-1层:
第i层(i=1、2、…、n-1)的起始位置为(0,i),随后列号col不变行号row递增(即向下填写),至row=i时折转;转折后,行号row不变列号col递减(即向左填写),至col=0时该层结束,在每一位置分别按递增值赋值给a[row][col]。
具体过程描述为:
a[0][0]=1;
num=2;
for(i=1;i<m;i++) // 方阵共m层
{
row=0; col=i; // 确定每层起始位置
a[row][col]= num++;
while(row<i) a[++row][col]=num++; // 先向下填
while(col>0) a[row][--col]=num++; // 再向左填
}
(2)源程序。
#include<stdio.h>
int main()
{
int i,m,num,row,col,a[20][20];
scanf("%d",&m);
a[0][0]=1;
num=2;
for (i=1;i<m;i++) // 方阵共m层
{
row=0; col=i;
a[row][col]=num++;
while(row<i) a[++row][col]=num++;
while(col>0) a[row][--col]=num++;
}
for (i=0;i<m;i++)
{
for (int j=0;j<m;j++)
printf("%4d",a[i][j]);
printf(" ");
}
return 0;
}
27-3 回转折叠方阵
问题描述
n阶回转折叠方阵是把起始数1置于方阵的左上角,然后从起始数开始递增,偶数层从第1行开始,先竖向下再折转向左;奇数层从第1列开始,先横向右再竖向上,呈首尾连接,层层折叠地排列为回转折叠方阵。例如,当n=4和n=5时的回转折叠方阵如下图4所示。

图4 回转折叠方阵
输入格式
一个正整数n(1≤n≤20)。
输出格式
N阶满足要求的回转折叠方阵。输出时共n行,每行n个数,每个数占4列。
输入样例
5
输出样例
1 2 9 10 25
4 3 8 11 24
5 6 7 12 23
16 15 14 13 22
17 18 19 20 21
(1)编程思路。
回转折叠方阵构造过程的奇数层(注意:由于数组下标从0开始,因此程序中层号也从0开始)与间断折叠构造过程相同,偶数层构造方法改变为:该层的起始位置为(i,0),随后行号row不变列号col递增(即向右填写),至col=i时折转;转折后,列号col不变行号row递减(即向上填写),至row=0时该层结束,在每一位置分别按递增值赋值给a[row][col]。具体描述为:
if (i%2==0)
{
row=i;col=0; // 确定偶数层的起始位置
a[row][col]=num++;
while(col<i) a[row][++col]=num++; // 先向右填
while(row>0) a[--row][col]=num++; // 再向上填
}
(2)源程序。
#include<stdio.h>
int main()
{
int i,m,num,row,col,a[20][20];
scanf("%d",&m);
a[0][0]=1;
num=2;
for(i=1;i<m;i++) // 方阵共m层
{
if (i%2==1)
{
row=0; col=i;
a[row][col]=num++;
while(row<i) a[++row][col]=num++;
while(col>0) a[row][--col]=num++;
}
else
{
row=i;col=0;
a[row][col]=num++;
while(col<i) a[row][++col]=num++;
while(row>0) a[--row][col]=num++;
}
}
for (i=0;i<m;i++)
{
for (int j=0;j<m;j++)
printf("%4d",a[i][j]);
printf(" ");
}
return 0;
}