4快速排序

内容

• 学习分而治之。
• 学习快速排序。

1.分而治之

D&C（devide and conquer）：一种著名的递归式问题解决方法。

1.1 农场主土地

假设农场主有一块土地（长1680米，宽640米），要将这块地均匀的分成方块，且分出的方块尽可能大。

欧几里得算法：适用于这块地的最大方块，也是适用于整块地的最大方块。
使用D&C解决问题的过程包括两个步骤：

• 1.找出基线条件，这种条件必须尽可能简单
• 2.不断将问题分解（或者说缩小规模），直到符合基线条件
  

按照这个思路

• 1.先寻找基线条件：方块长度等于宽度。
• 2.分解问题：每次先去除大的方块，针对剩下的区域进行递归，直到最后得到正方形。
  具体步骤：
  1680*640去掉2个边长640的正方形，得到640*400；
  640*400去掉边长400的正方形，得到40*240；
  400*240去掉边长240的正方形，得到240*160；
  240*160去掉160的正方形，得到160*80；
  160*80可以划分为2个边长80的正方形，符合基线条件，终止递归。
  

1.2 数组求和

D&C不是解决问题的算法，而是一种解决问题的思路。
给定一个数字数组[1, 2, 3, 4, 5, 6, 7, 8, 9]，进行求和。
方法一：使用循环很容易完成这种任务。

def sum(arr):
    total = 0
    for x in arr:
        total += x
    return total

方法二：使用递归函数来完成任务
第一步：找出基线条件
最简单的数组是空数组，其和是0
其次是包含1个元素的数组，其和是这个元素的值。
第二部：每次递归调用都必须离空数组更近一步。
这时只获取第一个数组的值，剩下的数组构成一个新的数组进行分解运算

def sum(arr):
    total=0
    if(len(arr))==0:
        total+=0
    else:
        total+=arr[0]
        total+=sum(arr[1:])
    return total
list=[1,2,3,4,5,6,7,8,9]
print(sum(list))    #45

1.3 练习

1.3.1编写一个递归函数来计算列表包含的元素数。
没有使用len(arr)，否则没啥意义了。

def sum(arr):
    total=0
    try:
        arr[0]
        total += 1
        total += sum(arr[1:])

    except IndexError as e:
        print("到达基线条件：数组为空")
    finally:
        return total
list=[1,2,3,4,5,6,7,8,9]
print(sum(list))

1.3.2找出列表中最大的数字

def getMax(arr):
    #数组长度为0，直接返回None
    value=None
    if (len(arr)>0):
        value=arr[0]
        value=digui(arr[1:],value)
    return value
def digui(arr,value):
    #基线条件，数组长度为1；否则就可以持续分割进行递归
    value = value if value > arr[0] else arr[0]
    if(len(arr)>1):
        #数组长度大于1，继续对比
        value=digui(arr[1:],value)
    return value

print("结果：",getMax([1,2,3,4,5,6,7,8,9,15]))
print("结果：",getMax([9,8,7,6,5,4,3,2,1]))
print("结果：",getMax([]))

2.1 快速排序

基线条件：最简单的数组是包含0个元素或1个元素的数组，不需要排序
递归条件：对于长度超过2的数组，使用D&C分解数组，直到满足基线条件。
首先，从数组中选择一个元素作为基准值。
然后分区，即找出比基准值大的元素和比基准值小的元素。然后会得到小于基准值的子数组、基准值、大于基准值的子数组。
递归，对长度大于2的子数组重复操作。

def quickSort(arr):
    if(len(arr)<2):
        return arr
    else:
        pivot = arr[0]
        less = [ i for i in arr[1:] if i<= pivot ]
        greater = [ i for i in arr[1:] if i>=pivot ]
        return quickSort(less)+[pivot]+quickSort(greater)
print(quickSort([10,5,2,3]))

3再谈大O表示法

快速排序的独特指出在于，其速度取决于选择的基准值。

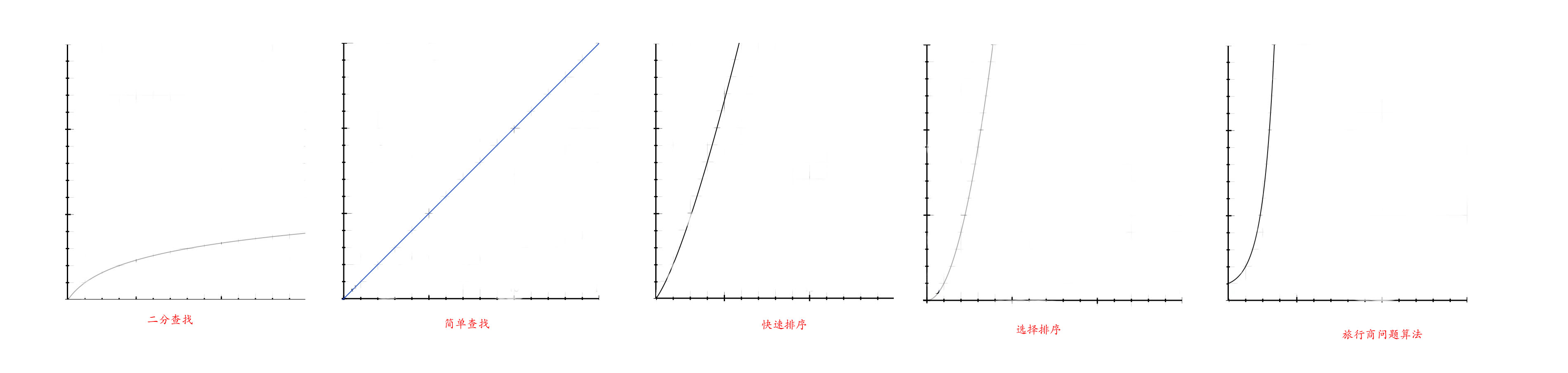
假设每秒执行10次

数组长度	二分查找	简单查找	快速查找	选择排序	旅行商问题算法
10	0.3秒	1秒	3.3秒	10秒	4.2天
100	0.6秒	10秒	66.4秒	16.6分	2.9*10149年
1000	1秒	100秒	996秒	27.7小时	1.27*102559年

3.1 算法中的常量

运行时间=c计算次数，c是算法所需的固定时间量。
如：简单查找每次用时10毫秒，二分查找每次用时1秒。
简单查找=cn，
二分查找=c*log₂n。
假设在40亿个元素的列表中查找，简单查找用时463天，二分查找用时32秒。
这是常量的影响取决于数组的长度。平均情况下，二分查找快得多。因为相对于最糟情况，遇上平均情况的可能性要大得多。

3.2 平均情况和最糟情况

快速排序的性能高度依赖于你选择的基准值。
假设有一个包含8个元素的数组[1, 2, 3, 4, 5, 6, 7, 8]
最糟情况：每次使用第一个元素作为基准值。数组并没有被分为两半，其中一个子数组一直为空。调用栈的长度为n，用时O(n)。
最佳情况：每次去中间的元素作为基准值。这样调用栈将短得多。调用栈的长度为O(log₂n)。