推荐算法-聚类-K-MEANS

    对于大型的推荐系统，直接上协同过滤或者矩阵分解的话可能存在计算复杂度过高的问题，这个时候可以考虑用聚类做处理，其实聚类本身在机器学习中也常用，属于是非监督学习的应用，我们有的只是一组组数据，最终我们要把它们分组，但是前期没有任何的先验知识告诉我们那个点是属于那个组的。

    当我们有足够的数据的时候可以考虑先用聚类做第一步处理，来缩减协同过滤的选择范围，从而降低复杂度。

    对了还想起来机器学习里面也经常用聚类的方式进行降维。这个在机器学习笔记部分后期我会整理。

    最终，每个聚类中的用户，都会收到为这个聚类计算出的推荐内容。聚类的话也有很多种方法时间，今天是整理最简单的那个姿势：K-MEANS

    K-MEANS聚类算法是非常常用的聚类算法。它出现在很多介绍性的数据科学和机器学习课程中。在代码中很容易理解和实现！

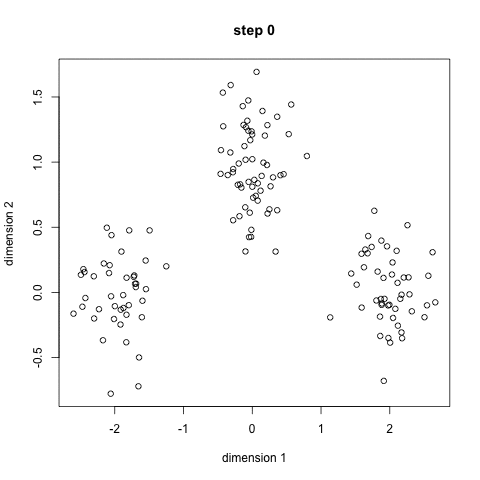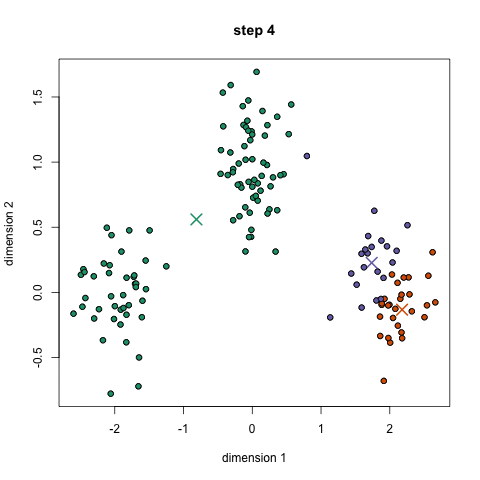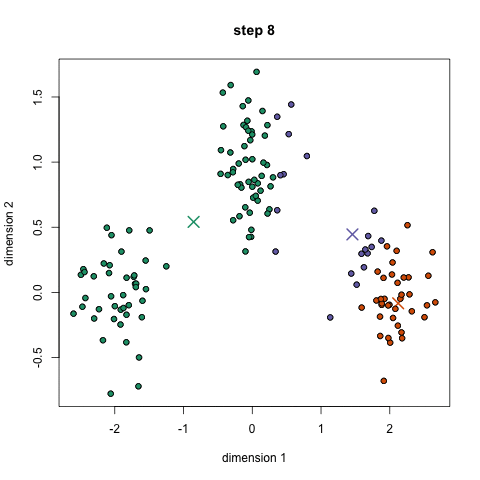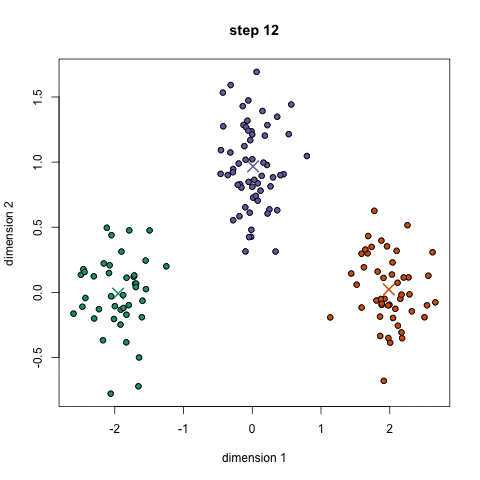
1. 首先，选择一些类/组来使用并随机地初始化它们各自的中心点。要想知道要使用的类的数量，最好快速地查看一下数据，并尝试识别任何不同的分组。中心点是与每个数据点向量相同长度的向量，在上面的图形中是“X”。
2. 每个数据点通过计算点可每个组中心之间的距离进行分类，然后将这个点分类为最接近它的组。
3. 基于这些分类点，我们通过去组中所有向量的均值来重新计算中心。
4. 对一组迭代重复这些步骤。你还可以选择随机初始化组中心几次，然后选择那些看起来对他提供好结果的来运行。

    K-MEANS聚类算法的优势在于它的速度非常快，因为我们所有的只是计算点和集群中心之间的距离，它有一个线性复杂度O(n)[注意不是整体的时间复杂度]。

另一方面，K-MEANS也有几个缺点。首先，你必须选择有多少组/类。这并不是不重要的事，理想情况下，我们希望它能帮我门解决这些问题，因为他的关键在于从数据中国的一些启示，K-MEANS也从随机的聚类中心开始，因此在不同的算法运行中可能产生不同的聚类结果。因此，结果可能是不可重复的，并且缺乏一致性。其他聚类方法更加一致。

    K-Medians是另一种与K-MEANS有关的聚类算法，除了使用均值的中间值来重新计算数组中心点以外，这种方法对于离散值的民高度较低（因为使用中值），但对于较大的数据集来说，它要慢得多，因为在计算中值向量时，每次迭代都需要进行排序。