LA4851餐厅（求好的坐标的个数）

题意：

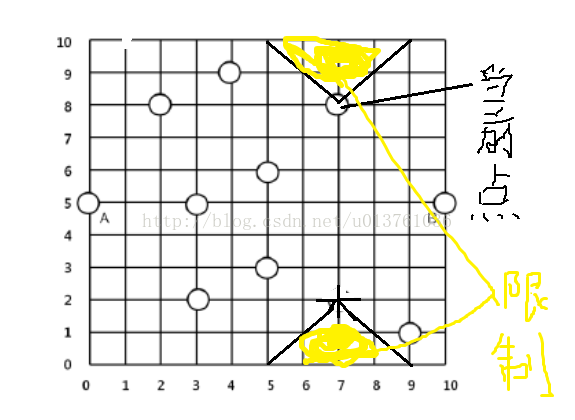
      有一个m*m的格子，左下角（0,0）右上角(m-1,m-1),网格里面有两个y坐标相同的宾馆（A,B），每个宾馆里面有一个餐厅，一共用n个餐厅，第1,2个都在宾馆里，3,4...在其他位置，你现在要在空余坐标上建立一个自己的餐厅，餐厅必须建立在最有利的位置上，什么样的位置算是有利的位置？如果你要在C这二个点建立一个餐厅，假如你要比D这个餐厅的位置有利那么你到A宾馆里里面的餐厅1的距离比C到这个宾馆的近，或者是到B的也行，只要有一个比C的近，那么你的位置就比C好，如果当前点想建立餐厅，那么必须必所有的餐厅的位置都好才行，问一共多有多少个好的位置。

思路：
       吭了好几个小时了，终于想出来了，对于每一个已经有的餐馆（包括第一个和第二个），他们会限制两个区域，分别是这两个区域（用右上方这个点举例）：
每个点都有这样类此的以AB连线对称的两个限制区域，我们把所有区域叠加起来，最后剩下的就是可行的区域，叠加的时候也很简单，我们枚举x1--x2的所有x,Yu[x]表示x节点在AB连线上方的最小限制值，Yd[x]是下方的最大限制值，Y[x] = minn(Yu[x] - y ,Yd[x] - y)，表示的是在x这个点的这一竖列的最大非限制距离，然后就是简单更新，具体细节看下面代码。




#include<stdio.h>


#define N 66000
#define INF 100000000


int maxx(int x ,int y)
{
   return x > y ? x : y;
}


int minn(int x ,int y)
{
   return x < y ? x : y;
}


int Yu[N] ,Yd[N] ,Y[N];


int main ()
{
   int t ,n ,m ,i ,x ,y ,x1 ,x2 ,y1 ,y2;
   scanf("%d" ,&t);
   while(t--)
   {
      scanf("%d %d" ,&m ,&n);
      scanf("%d %d" ,&x1 ,&y1);
      scanf("%d %d" ,&x2 ,&y2);
      if(x1 > x2) x = x1 ,x1 = x2 ,x2 = x;
      for(i = x1 ;i <= x2 ;i ++)
      Yd[i] = -INF ,Yu[i] = INF;
      for(i = 3 ;i <= n ;i ++)
      {
         scanf("%d %d" ,&x ,&y);
         if(y >= y1) Yu[x] = minn(Yu[x] ,y);
         if(y <= y1) Yd[x] = maxx(Yd[x] ,y);
      }
      Y[x1] = Y[x2] = 0;
      for(i = x1 + 1 ;i < x2 ;i ++)
      Y[i] = minn(Yu[i] - y1 ,y1 - Yd[i]);
      
      for(i = x1 + 1 ;i < x2 ;i ++)
      Y[i] = minn(Y[i-1] + 1 ,Y[i]);
      
      for(i = x2 - 1 ;i > x1 ;i --)
      Y[i] = minn(Y[i+1] + 1  ,Y[i]);
      
      long long Ans = 0;
      for(i = x1 + 1 ;i < x2 ;i ++)
      {
         if(Y[i])
         {
            Ans ++;
            Ans += (long long)minn(m - 1 - y1 ,Y[i] - 1);//防止出现INF
            Ans += (long long)minn(Y[i] - 1,y1);//防止出现INF
         }
      }
      printf("%lld " ,Ans);
   }
   return 0;
}