LCS(Longest Common Subsequence)最长公共子序列

最长公共子序列（LCS）是一个在一个序列集合中（通常为两个序列）用来查找所有序列中最长子序列的问题。这与查找最长公共子串的问题不同的地方是：子序列不需要在原序列中占用连续的位置 。最长公共子序列问题是一个经典的计算机科学问题，也是数据比较程序，比如Diff工具，和生物信息学应用的基础。它也被广泛地应用在版本控制，比如Git用来调和文件之间的改变。

最长公共子串问题是寻找两个或多个已知字符串最长的子串。此问题与最长公共子序列问题的区别在于子序列不必是连续的，而子串却必须是连续的。

定义：一个数列，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则称为已知序列的最长公共子序列。

两个序列的解法

最长公共子序列问题存在最优子结构：这个问题可以分解成更小，更简单的“子问题”，这个子问题可以分成更多的子问题，因此整个问题就变得简单了。最长公共子序列问题的子问题的解是可以重复使用的，也就是说，更高级别的子问题通常会重用低级子问题的解。拥有这个两个属性的问题可以使用动态规划算法来解决，这样子问题的解就可以被储存起来，而不用重复计算。这个过程需要在一个表中储存同一级别的子问题的解，因此这个解可以被更高级的子问题使用。

 

核心数组表示{displaystyle X}的第位和{displaystyle Y}的第{displaystyle j}位之前的最长公共子序列的长度，则有状态转移方程：

当x[i+1]==y[j+1]时，f[i+1][j+1]=f[i][j]+1;//比之前多了一个

否则f[i+1][j+1]=max(f[i][j + 1],f[i + 1][j])；

 实例

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例 1:

输入：text1 = "abcde", text2 = "ace"
输出：3
解释：最长公共子序列是 "ace"，它的长度为 3。
示例 2:

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc"，它的长度为 3。
示例 3:

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0。
 

提示:

1 <= text1.length <= 1000
1 <= text2.length <= 1000
输入的字符串只含有小写英文字符。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-common-subsequence
示例1的状态表：

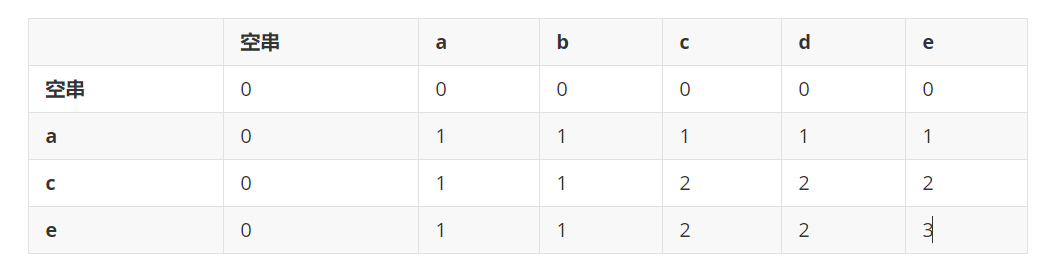
题解：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
     int len1 = text1.length();
     int len2 = text2.length();
     char[] chars1 = text1.toCharArray();
     char[] chars2 = text2.toCharArray();
    //注意是之前串长度加1，有一行和一列是空串
     int [][]dp = new int[len1+1][len2+1];
     for(int i=1;i<=len1;i++){
         for(int j=1;j<=len2;j++){
             if(chars1[i-1] == chars2[j-1]){
                 dp[i][j] = dp[i-1][j-1]+1;
             }else{
                 dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j]);
             }
         }
     }
     return dp[len1][len2];
     
    }
}