2019CCPC秦皇岛 E题 Escape（网络流）

Escape

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 16    Accepted Submission(s): 12

Problem Description

Given a maze of size n×m. The rows are numbered 1, 2, · · · , n from top to bottom while the columns are numbered 1, 2, · · · , m from left to right, which means that (1, 1) is the top-left corner and that (n, m) is the bottom-right corner. And for each cell of size 1 × 1, it is either blank or blocked.
There are a robots above the maze. For i-th robot, it is initially positioned exactly above the cell (1, pi), which can be described as (0, pi). And the initial moving direction of the robots are all downward, which can be written as (1, 0) in the vector form.
Also, there are b exits below the maze. For i-th exit, it is positioned exactly below the cell (n, ei), which can be described as (n + 1, ei).
Now, you want to let the robots escape from the maze by reaching one of the exits. However, the robots are only able to go straight along their moving directions and can’t make a turn. So you should set some turning devices on some blank cells in the maze to help the robots make turns.
There are 4 types of turning devices:

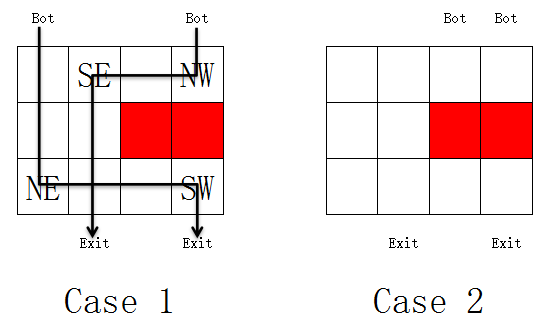
• “NE-devices” : make the robots coming from above go rightward, and make the robots coming from right go upward. Coming from left or below is illegal.

• “NW-devices” : make the robots coming from above go leftward, and make the robots coming from left go upward. Coming from right or below is illegal.

• “SE-devices” : make the robots coming from below go rightward, and make the robots coming from right go downward. Coming from left or above is illegal.

• “SW-devices” : make the robots coming from below go leftward, and make the robots coming from left go downward. Coming from right or above is illegal.

For each cell, the number of turning devices on it can not exceed 1. And collisions between the robots are ignored, which allows multiple robots to visit one same cell even at the same time.
You want to know if there exists some schemes to set turning devices so that all the a robots can reach one of the b exits after making a finite number of moves without passing a blocked cell or passing a turning device illegally or going out of boundary(except the initial position and the exit).
If the answer is yes, print “Yes” in a single line, or print “No” if the answer is no.

 

Input

The first line contains one positive integer T (1 ≤ T ≤ 10), denoting the number of test cases.
For each test case:
The first line contains four positive integers n, m, a, b (1 ≤ n, m ≤ 100, 1 ≤ a, b ≤ m), denoting the number of rows and the number of columns in the maze, the number of robots and the number of exits respectively.
Next n lines each contains a string of length m containing only “0” or “1”, denoting the initial maze, where cell (i, j) is blank if the j-th character in i-th string is “0”, while cell (i, j) is blocked if the j-th character in i-th string is “1”.
The next line contains a integers pi (1 ≤ pi ≤ m), denoting the initial positions (0, pi) of the robots.
The next line contains b integers ei (1 ≤ ei ≤ m), denoting the positions (n + 1, ei) of the exits.
It is guaranteed that all pis are pairwise distinct and that all eis are also pairwise distinct.

 

Output

Output T lines each contains a string “Yes” or “No”, denoting the answer to corresponding test case.

 

Sample Input

2 3 4 2 2 0000 0011 0000 1 4 2 4 3 4 2 2 0000 0011 0000 3 4 2 4

 

Sample Output

Yes No

Hint

 

Source

642ccpcQHD

---

题解：

每个格子的水平方向和竖直方向都只能被使用一次，因为两个机器人的路径不可能合并，也不可能迎面相撞。如果一个格子没有放转弯装置，则可以被水平穿过一次，竖直穿过一次。如果一个格子放了转弯装置，则这个格子只能被一个机器人经过一次。所以对于所有非障碍格子，可以拆成水平点和竖直点，每个点限流 1，上下相邻的格子连竖直点（竖直直行），左右相邻的格子连水平点（水平直行），格子内部的水平点和竖直点互相相连（转弯），源连向起点的竖直点，出口的竖直点连向汇，跑最大流，如果最大流 = 机器人个数，则输出 Yes，否则输出 No。

 

参考代码：

#include<bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
const int N=40010,M=1000010;
int T,n,m,a,b,h[N],s,t,base;
char g[110][110];
int head[N],nex[M],w[M],to[M],tot;
inline void ade(int a,int b,int c)
{
    to[++tot]=b; 
    nex[tot]=head[a]; 
    w[tot]=c; 
    head[a]=tot;
}
inline void add(int a,int b,int c)
{
    ade(a,b,c);    
    ade(b,a,0);
}
inline int id(int x,int y){return m*x+y;}
inline int bfs()
{
    memset(h,0,sizeof h);    
    h[s]=1;    
    queue<int> q; q.push(s);
    while(q.size())
    {
        int u=q.front(); q.pop();
        for(int i=head[u];i;i=nex[i])
        {
            if(!h[to[i]]&&w[i])
            {
                h[to[i]]=h[u]+1;    
                q.push(to[i]);
            }
        }
    }
    return h[t];
}
int dfs(int x,int f)
{
    if(x==t) return f;    
    int fl=0;
    for(int i=head[x];i&&f;i=nex[i])
    {
        if(h[to[i]]==h[x]+1&&w[i])
        {
            int mi=dfs(to[i],min(w[i],f));
            w[i]-=mi; w[i^1]+=mi; fl+=mi; f-=mi;
        }
    }
    if(!fl)    h[x]=-1;
    return fl;
}
int dinic()
{
    int res=0;
    while(bfs()) res+=dfs(s,inf);
    return res;    
}
signed main()
{
    cin>>T;
    while(T--)
    {
        tot=1;    
        memset(head,0,sizeof head);
        cin>>n>>m>>a>>b;    
        base=(n+2)*m;    t=base*2;
        for(int i=1;i<=n;i++)    scanf("%s",g[i]+1);
        for(int i=1;i<=a;i++)
        {
            int x;    scanf("%d",&x);    g[0][x]='1';
            add(s,id(0,x),1);    add(id(0,x),id(1,x),1);
        }
        for(int i=1;i<=b;i++)
        {
            int x;    scanf("%d",&x);    
            g[n+1][x]='1';
            add(id(n+1,x),t,inf);    
            add(id(n,x),id(n+1,x),inf);
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                if(g[i][j]=='1') continue;
                if(i>1)    add(id(i,j),id(i-1,j),1);
                if(i<n)    add(id(i,j),id(i+1,j),1);
                if(j>1)    add(id(i,j)+base,id(i,j-1)+base,1);
                if(j<m)    add(id(i,j)+base,id(i,j+1)+base,1);
                add(id(i,j),id(i,j)+base,1);add(id(i,j)+base,id(i,j),1);
            }
        }
        puts(dinic()==a?"Yes":"No");
    }
    return 0;
}