拓展kmp是对KMP算法的扩展,它解决如下问题:
定义母串S,和字串T,设S的长度为n,T的长度为m,求T与S的每一个后缀的最长公共前缀,也就是说,设extend数组,extend[i]表示T与S[i,n-1]的最长公共前缀,要求出所有extend[i](0<=i<n)。
注意到,如果有一个位置extend[i]=m,则表示T在S中出现,而且是在位置i出现,这就是标准的KMP问题,所以说拓展kmp是对KMP算法的扩展,所以一般将它称为扩展KMP算法。
下面举一个例子,S=”aaaabaa”,T=”aaaaa”,首先,计算extend[0]时,需要进行5次匹配,直到发生失配。
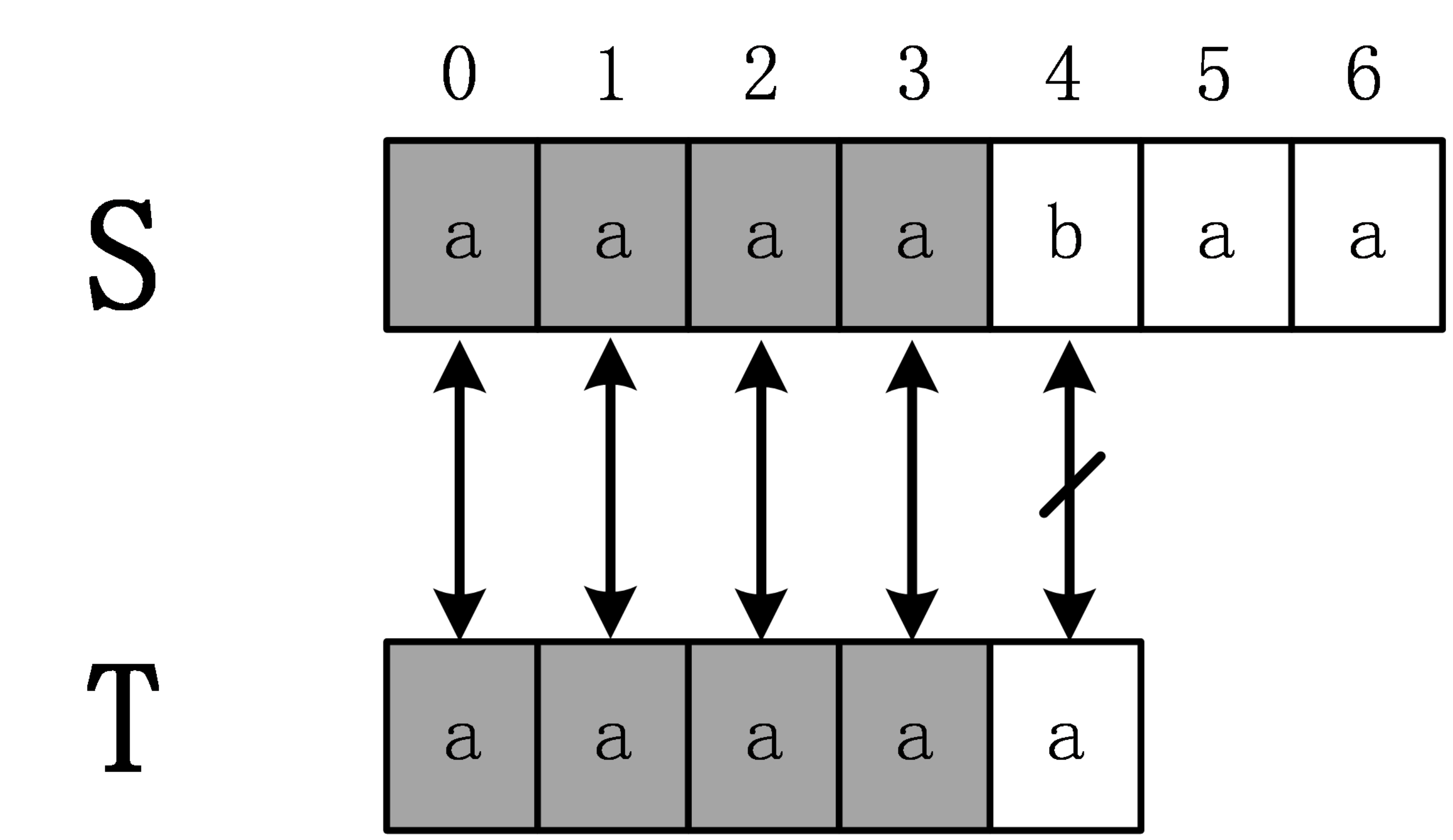
从而得知extend[0]=4,下面计算extend[1],在计算extend[1]时,是否还需要像计算extend[0]时从头开始匹配呢?答案是否定的,因为通过计算extend[0]=4,从而可以得出S[0,3]=T[0,3],进一步可以得到 S[1,3]=T[1,3],计算extend[1]时,事实上是从S[1]开始匹配,设辅助数组next[i]表示T[i,m-1]和T的最长公共前缀长度。在这个例子中,next[1]=4,即T[0,3]=T[1,4],进一步得到T[1,3]=T[0,2],所以S[1,3]=T[0,2],所以在计算extend[1]时,通过extend[0]的计算,已经知道S[1,3]=T[0,2],所以前面3个字符已经不需要匹配,直接匹配S[4]和T[3]即可,这时一次就发生失配,所以extend[1]=3。这个例子很有代表性,有兴趣的读者可以继续计算完剩下的extend数组。
1. 拓展kmp算法一般步骤
通过上面的例子,事实上已经体现了拓展kmp算法的思想,下面来描述拓展kmp算法的一般步骤。
首先我们从左到右依次计算extend数组,在某一时刻,设extend[0...k]已经计算完毕,并且之前匹配过程中所达到的最远位置为P,所谓最远位置,严格来说就是i+extend[i]-1的最大值(0<=i<=k),并且设取这个最大值的位置为po,如在上一个例子中,计算extend[1]时,P=3,po=0。
现在要计算extend[k+1],根据extend数组的定义,可以推断出S[po,P]=T[0,P-po],从而得到 S[k+1,P]=T[k-po+1,P-po],令len=next[k-po+1],(回忆下next数组的定义),分两种情况讨论:
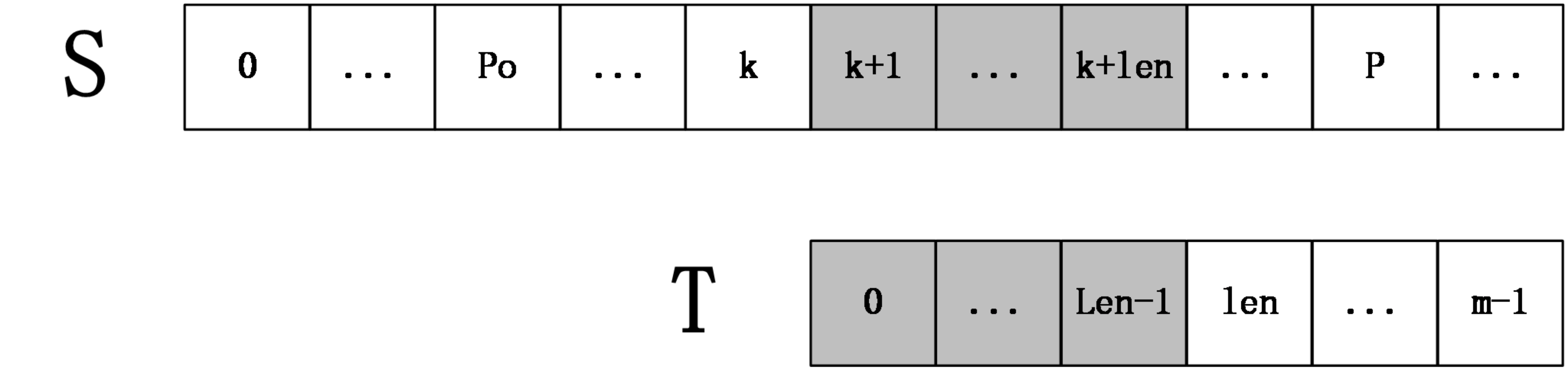
第一种情况:k+len<P
如下图所示:
上图中,S[k+1,k+len]=T[0,len-1],然后S[k+len+1]一定不等于T[len],因为如果它们相等,则有S[k+1,k+len+1]=T[k+po+1,k+po+len+1]=T[0,len],那么next[k+po+1]=len+1,这和next数组的定义不符(next[i]表示T[i,m-1]和T的最长公共前缀长度),所以在这种情况下,不用进行任何匹配,就知道extend[k+1]=len。
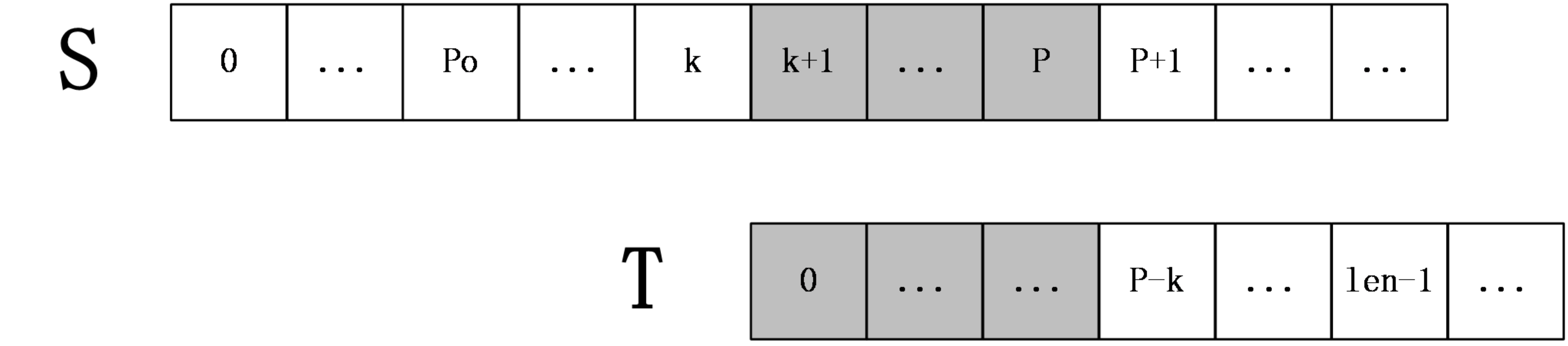
第二种情况: k+len>=P
如下图:
上图中,S[p+1]之后的字符都是未知的,也就是还未进行过匹配的字符串,所以在这种情况下,就要从S[P+1]和T[P-k+1]开始一一匹配,直到发生失配为止,当匹配完成后,如果得到的extend[k+1]+(k+1)大于P则要更新未知P和po。
至此,拓展kmp算法的过程已经描述完成,细心地读者可能会发现,next数组是如何计算还没有进行说明,事实上,计算next数组的过程和计算extend[i]的过程完全一样,将它看成是以T为母串,T为字串的特殊的拓展kmp算法匹配就可以了,计算过程中的next数组全是已经计算过的,所以按照上述介绍的算法计算next数组即可,这里不再赘述。
2. 时间复杂度分析
下面来分析一下算法的时间复杂度,通过上面的算法介绍可以知道,对于第一种情况,无需做任何匹配即可计算出extend[i],对于第二种情况,都是从未被匹配的位置开始匹配,匹配过的位置不再匹配,也就是说对于母串的每一个位置,都只匹配了一次,所以算法总体时间复杂度是O(n)的,同时为了计算辅助数组next[i]需要先对字串T进行一次拓展kmp算法处理,所以拓展kmp算法的总体复杂度为O(n+m)的。其中n为母串的长度,m为子串的长度。
下面是拓展kmp算法的一道例题。
给你一个字符串ss,然后再给你nn个询问,第ii个询问给你一个数字kk和一个字符串mm
这个询问的答案是tt的最小长度,其中tt是ss的子串,且tt中必须出现kk个mm
Input
第一行一个字符串SS
第二行数字QQ,代表询问次数
后面每一行一个kk和mm,代表依次询问
数据保证所有字母均为小写字母
(1≤|s|≤105)(1≤|s|≤105)
(1≤Q≤105)(1≤Q≤105)
(1≤ki≤|s|)(1≤ki≤|s|)
所有询问长度加起来小于100000100000
保证所有字符串不相同
Output
QQ行,每行代表一个询问的答案
无解请输出−1−1
Sample input and output
| Sample Input | Sample Output |
|---|---|
aaaaa 5 3 a 3 aa 2 aaa 3 aaaa 1 aaaaa | 3 4 4 -1 5 |
abbb 7 4 b 1 ab 3 bb 1 abb 2 bbb 1 a 2 abbb | -1 2 -1 3 -1 1 -1 |
代码为:
#include<bits/stdc++.h>
using namespace std;
const int maxn=100010;
int net[maxn],ex[maxn];
char s1[maxn],s2[maxn];
void GETNEXT(char *str)
{
int i=0,j,po,len=strlen(str);
net[0]=len;
while(str[i]==str[i+1]&&i+1<len)
i++;
net[1]=i;
po=1;
for(i=2;i<len;i++)
{
if(net[i-po]+i<net[po]+po)
net[i]=net[i-po];
else
{
j=net[po]+po-i;
if(j<0)j=0;
while(i+j<len&&str[j]==str[j+i])
j++;
net[i]=j;
po=i;
}
}
}
void EXKMP(char *s1,char *s2)
{
int i=0,j,po,len=strlen(s1),l2=strlen(s2);
GETNEXT(s2);
while(s1[i]==s2[i]&&i<l2&&i<len)
i++;
ex[0]=i;
po=0;
for(i=1;i<len;i++)
{
if(net[i-po]+i<ex[po]+po)
ex[i]=net[i-po];
else
{
j=ex[po]+po-i;
if(j<0)j=0;
while(i+j<len&&j<l2&&s1[j+i]==s2[j])
j++;
ex[i]=j;
po=i;
}
}
}
int main()
{
ios::sync_with_stdio(false);//用scanf,printf TLE 。。。
cin.tie(0);
int n,k,len;
cin>>s1;
len=strlen(s1);
cin>>n;
while(n--)
{
cin>>k>>s2;
int len2=strlen(s2),sum=0,temp,cnt=-1;
EXKMP(s1,s2);
for(int i=0;i<len;i++)
{
if(ex[i]==len2)
{
sum++;
if(sum==1) temp=i;
if(sum==k)
{
cnt=i-temp+len2;
break;
}
}
}
cout<<cnt<<endl;
}
return 0;
}