lg4705:原式经过转化可以变成卷积的形式,但是这样子也很难做。
题目要我们求$frac{a[i]^v}{i!}$,需要把它变为生成函数
后面的东西a[i]^v,它的生成函数是$frac{1}{1-a[i]x}$
这道题可以构造2个ln函数,然后答案就成为了n-x*(ln(1-a[i]x))'
使用分治fft计算1-a[i]*x后ln,求导,用n减去,每个元素乘以i!,最后卷积即可。
lg4389:
这道题是一个背包问题。
考虑写出每种物品的普通生成函数:是$1+x^i+x^{2i}+x^{3i}+....$
原因是这道题物品可以选择无数次。
这个函数就是$frac{1}{1-x^i}$
可以使用分治fft把所有的多项式乘起来,但是无法通过此题。
实际上这道题可以先ln,再指数相加,最后exp,但是也过不了这道题。需要挖掘这个函数的性质。
分治fft的做法扩展难度较大,所以考虑扩展ln做法。
把函数求导一下,则根据复合函数求导法则,假设右边是g(x),f(x)=1-x^i则$g(x)'=frac{f'(x)}{f(x)}$
把原式使用生成函数展开。则$g(x)'=-sum vx^{v-1+vi}$
还原函数(不用导数了),变成$g(x)=-sum frac{vx^{v+vi}}{v+vi}$
这个式子还是不好看,可以把i从0枚举变成从1枚举,上面下面都除以v,变成$g(x)=-sum frac{x^{vi}}{i}$
可以统计每种物品的个数,再加上对应的系数,exp回来,最终求逆即可。
这道题的思路十分经典,值得学习。
lg5162
先dp,再构造指数型生成函数计算即可。要用多项式求逆。
lg5219
这道题要使用prufer序列做。
uoj79
一般图最大匹配。
一般图最大匹配与二分图最大匹配相似,但是多了处理奇环的过程。
最大匹配的思想是:每次寻找一个未被匹配的点,走到另一个未被匹配的点,翻转路径上的所有边。
可以证明这样子翻转若干次直到没有增广路时,是最优的。
在二分图这样子一定不会经过重复的点。(画一下图可以知道)
但是一般图中有奇环,所以可能经过重复的点,算法会死循环。
所以要处理奇环。
BFS整张图,把队列中存在过的点染黑,黑点的匹配点染白。
每次从队列中取出一个点。枚举它的出点,设为v
若v在当前bfs中未被访问过:则找到了一个匹配,直接返回。
否则把它的匹配点插入队列。
若v被访问过,则发现找到了一个环。
如果这个环是偶环,则不用考虑,一定不会走重复点。
但是如果这个环是奇环,则要处理。
设环边为(u,v),lca为h
把这个环缩起来并且再次寻找增广路。
证明:如果原图为g,缩点后的图为g'
则要证明g中的增广路,g'也有
g'有的增广路,g中也有。
当g有增广路,发现h->s上的第一条边一定是匹配边。
如果不是,可以走到一个环上的未盖点继续增广。
设s->h这个路径为p。
令gs,g's为g,g'把这条路径取反后的结果。显然匹配大小不变。
若g存在增广路,则g的最大匹配值应该更大,gs的最大匹配值也应该更大,所以gs也有增广路。
设gs的增广路为c,则如果c没有经过旧环,则g's也包含c
否则,让g's的这一条增广路c走到h,则发现肯定有一种走法可以走交错边。
因为g's的匹配数和g'相同,所以根据增广路定理,g'也有增广路。
当g'有增广路,如果没走新点,则g中也有。
如果走了新点,则走新点肯定是走过匹配边,非匹配边。
匹配边肯定是和h相连的。
由于环是奇环,且匹配边交错,所以一定可以找到一种走法走到h。
uoj171
这道题是一个一般图最大匹配建模,十分巧妙。
建模的方法是:对于每个篮子拆成3个点,这3个点之间两两连边。
对于每个点向它能被放置的篮子连边。
然后求一般图最大匹配,答案再减去n。
原因是:
当一个篮子没有连匹配边(没有球被放在这个篮子里),则贡献为1
当一个篮子连了1条匹配边(有1个球被放在这个篮子里),则贡献为2
当一个篮子连了2条匹配边(有2个球被放在这个篮子里),则贡献为2
当一个篮子连了3条匹配边(有3个球被放在这个篮子里),则贡献为3
减去连的匹配边的个数。(它们的和为球的个数),
当一个篮子没有连匹配边(没有球被放在这个篮子里),则贡献为1
当一个篮子连了1条匹配边(有1个球被放在这个篮子里),则贡献为1
当一个篮子连了2条匹配边(有2个球被放在这个篮子里),则贡献为0
当一个篮子连了3条匹配边(有3个球被放在这个篮子里),则贡献为0
恰好为题目所要求的贡献。
注意,要从大->小增广,这样子在增广的过程中不会让大的点(即球点)失配(观察翻转边的过程可得)。

#include<bits/stdc++.h> using namespace std; #define N 1010 int h[N],v[N*N*4],nxt[N*N*4],ec,n,m,x,y,ct,pr[N],mt[N],id[N],p[N],vi[N],t,e; void add(int x,int y){v[++ec]=y;nxt[ec]=h[x];h[x]=ec;} int fd(int x){return p[x]==x?x:p[x]=fd(p[x]);} void adj(int x,int y){add(x,y);add(y,x);} queue<int>q; int lca(int x,int y){ ct++; x=fd(x); y=fd(y); while(id[x]!=ct){ id[x]=ct; x=fd(pr[mt[x]]); if(y)swap(x,y); } return x; } inline char nc(){ static char buf[1000000],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++; } inline int rd(){ char ch=nc();int sum=0; while(!(ch>='0'&&ch<='9'))ch=nc(); while(ch>='0'&&ch<='9')sum=sum*10+ch-48,ch=nc(); return sum; } void bb(int x,int y,int z){ while(fd(x)!=z){ pr[x]=y; y=mt[x]; if(vi[y]==2){ vi[y]=1; q.push(y); } if(fd(x)==x)p[x]=z; if(fd(y)==y)p[y]=z; x=pr[y]; } } int ag(int s){ memset(pr,0,sizeof(pr)); memset(vi,0,sizeof(vi)); vi[s]=1; while(!q.empty())q.pop(); q.push(s); for(int i=1;i<=n+m*3;i++)p[i]=i; while(!q.empty()){ int x=q.front(); q.pop(); for(int i=h[x];i;i=nxt[i]){ if(fd(x)==fd(v[i])||vi[v[i]]==2)continue; if(!vi[v[i]]){ vi[v[i]]=2; pr[v[i]]=x; if(!mt[v[i]]){ int x=v[i],la; for(;x;x=la){ la=mt[pr[x]]; mt[x]=pr[x]; mt[pr[x]]=x; } return 1; } vi[mt[v[i]]]=1; q.push(mt[v[i]]); } else{ int d=lca(x,v[i]); bb(x,v[i],d); bb(v[i],x,d); } } } return 0; } int main(){ t=rd(); while(t--){ memset(h,0,sizeof(h)); memset(mt,0,sizeof(mt)); memset(id,0,sizeof(id)); ec=0; n=rd(); m=rd(); e=rd(); for(int i=1;i<=m;i++){ adj(i*3-2,i*3-1); adj(i*3-1,i*3); adj(i*3,i*3-2); } while(e--){ x=rd(); y=rd(); adj(x+3*m,y*3-2); adj(x+3*m,y*3-1); adj(x+3*m,y*3); } int r=0; for(int i=n+m*3;i;i--) if(!mt[i])r+=ag(i); cout<<r-n<<' '; for(int i=m*3+1;i<=n+m*3;i++) cout<<ceil((double)mt[i]/3.0)<<' '; cout<<' '; } }
bzoj1135
hall定理的运用。
这道题中,第i个人可以穿i~i+d的鞋子,所以实际上这道题就是个二分图匹配模型。
右边有n个点,表示鞋子,左边初始没有点,每次增加/减少一些点。
操作有2种:增加k个点,类型为i,这k个点向i->i+d连边,然后要求二分图是否有完全匹配。
减少k个点,类型为i,这k个点向i->i+d连边,然后要求二分图是否有完全匹配。
这样子显然是会超时的,要考虑hall定理。
发现每一种人可以当做整体考虑。因为这些人对应的右边的点数都是一样的,都是d,若取这些人的子集进行判断,则对于右边的点数还是d,但是左边的点数减少,更符合要求。
发现只需要对于每个区间考虑是否合法即可。因为如果选出一些连通块,则实际上要求就是这些连通块是否分别满足hall定理。
因为把这些连通块和它对应的点(设为t)的大小加起来,大小>=这些连通块全体对应
如果这些连通块(大小设为s)全都分别满足要求,且加起来不满足要求,由于右边的连通块是有重复的(设值为v)
则要满足s<=v<=t,s>=v,矛盾。所以只要分别判定每个连通块(就是所有区间)是否合法即可。
如果中间区间有交的话,则把中间的补进来,二分图左边的点数会增大,右边不变,限制更强。
所以只需要判定每个区间是否合法即可。
可以得到s<=(r-l+1+d)*k
把所有数减去k,则得到s<=d*k
这个用线段树维护最大子段和即可。
lg4002
prufer序列:prufer序列和一棵无向完全图的生成树一一对应。
构造prufer序列的方法是:从prufer序列中选出一个叶子节点,且编号最小,删除这个叶子节点,把它添加到答案序列的末尾。
一直这样,直到树上只剩下2个节点,答案序列的大小就为n-2,得到了prufer序列。
这个序列有2个性质:每个元素的取值可以为任意(这说明无根树的大小有n^(n-2)个),每个节点的度数为它在这个序列的出现次数+1。
这道题主要要使用第二个性质。
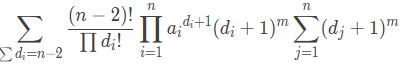
这个公式描述了初始的答案。
d[i]表示第i个元素的出现次数。前面的表示这i个元素可以被分布在这个序列的任何位置。后面的a[i]^(d[i]+1)表示每个连通块大小伟a[i],可以连出d[i]+1条边,后面的式子为权值的定义。
如果把一个a[i]提取出来的话,则公式变为:

这个公式转换了枚举顺序。
前面的式子(n-2)!*a[i]可以O(n)计算,后面的式子如果硬算时间复杂度很高。所以要使用生成函数优化。
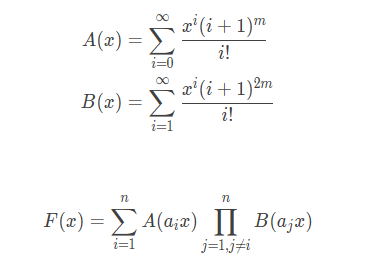
构造2个生成函数a,b,且定义f
f实际上可以被变成除法的形式:

后面的可以使用套路,先ln,再转成加法,最后exp回来,变成:
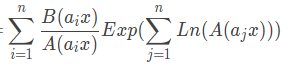
但是每个式子还要乘以一个系数,类似lg4705那样做即可。

#include<bits/stdc++.h> using namespace std; #define mo 998244353 #define N 5000010 #define ll unsigned long long #define int long long #define pl vector<int> int qp(int x,int y){ int r=1; for(;y;y>>=1,x=1ll*x*x%mo) if(y&1)r=1ll*r*x%mo; return r; } int rev[N],v,le,w[N],p[N]; void deb(pl x){ for(int i:x)cout<<i<<' '; puts(""); } void init(int n){ v=1; le=0; while(v<n)le++,v*=2; for(int i=0;i<v;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(le-1)); int g=qp(3,(mo-1)/v); w[v/2]=1; for(int i=v/2+1;i<v;i++) w[i]=1ull*w[i-1]*g%mo; for(int i=v/2-1;~i;i--) w[i]=w[i*2]; } void fft(int v,pl &a,int t){ static unsigned long long b[N]; int s=le-__builtin_ctz(v); for(int i=0;i<v;i++) b[rev[i]>>s]=a[i]; int c=0; w[0]=1; for(int i=1;i<v;i*=2,c++) for(int r=i*2,j=0;j<v;j+=r) for(int k=0;k<i;k++){ int tx=b[j+i+k]*w[k+i]%mo; b[j+i+k]=b[j+k]+mo-tx; b[j+k]+=tx; } for(int i=0;i<v;i++) a[i]=b[i]%mo; if(t==0)return; int iv=qp(v,mo-2); for(int i=0;i<v;i++) a[i]=1ull*a[i]*iv%mo; a.resize(v); reverse(a.begin()+1,a.end()); } pl operator *(pl x,pl y){ int s=x.size()+y.size()-1; if(x.size()<=20||y.size()<=20){ pl r; r.resize(s); for(int i=0;i<x.size();i++) for(int j=0;j<y.size();j++) r[i+j]=(r[i+j]+x[i]*y[j])%mo; return r; } init(s); x.resize(v); y.resize(v); fft(v,x,0); fft(v,y,0); //deb(x); //deb(y); for(int i=0;i<v;i++) x[i]=x[i]*y[i]%mo; fft(v,x,1); x.resize(s); return x; } void inv(int n,pl &b,pl &a){ if(n==1){ b[0]=qp(a[0],mo-2); return; } inv((n+1)/2,b,a); static pl c; init(n*2); c.resize(v); b.resize(v); for(int i=0;i<n;i++) c[i]=a[i]; fft(v,c,0); //deb(c); fft(v,b,0); //deb(b); for(int i=0;i<v;i++) b[i]=1ll*(2ll-1ll*c[i]*b[i]%mo+mo)%mo*b[i]%mo; //deb(b); fft(v,b,1); b.resize(n); //deb(b); } void ad(pl &x,pl y,int l){ x.resize(max((int)x.size(),(int)y.size()+l)); for(int i=0;i<y.size();i++) x[i+l]=(x[i+l]+y[i])%mo; } pl operator +(pl x,pl y){ ad(x,y,0); return x; } pl iv(pl x){ pl y; int n=x.size(); y.resize(n); inv(n,y,x); y.resize(n); return y; } pl operator -(pl x,pl y){ int s=max(x.size(),y.size()); x.resize(s); y.resize(s); for(int i=0;i<s;i++) x[i]=(x[i]-y[i]+mo)%mo; return x; } pl qd(pl x){ pl y; int n=x.size(); y.resize(n-1); //deb(x); for(int i=0;i<n-1;i++) y[i]=x[i+1]*(i+1)%mo; //deb(y); return y; } pl jf(pl x){ int n=x.size(); pl y; y.resize(n+1); for(int i=1;i<=n;i++) y[i]=x[i-1]*qp(i,mo-2)%mo; return y; } pl ln(pl x){ int n=x.size(); pl y=qd(x),z=iv(x); y=y*z; y=jf(y); y.resize(n); return y; } inline char nc(){ static char buf[500000],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,500000,stdin),p1==p2)?EOF:*p1++; } inline int rd(){ char ch=nc();int sum=0; while(!(ch>='0'&&ch<='9'))ch=nc(); while(ch>='0'&&ch<='9')sum=sum*10+ch-48,ch=nc(); return sum; } char bf[100]; void wr(int x){ if(!x){ putchar('0'); putchar(' '); return; } int ct=0; while(x){ bf[++ct]=x%10; x/=10; } for(int i=ct;i;i--) putchar(bf[i]+'0'); putchar(' '); } void gt(int n,pl &y,pl x){ if(n==1){ y.resize(1); y[0]=1; return; } gt((n+1)/2,y,x); pl z=x,a; z.resize(n); y.resize(n); a.resize(1); a[0]=1; y=y*(a-ln(y)+z); y.resize(n); } pl ep(pl x){ pl y; int n=x.size(); gt(n,y,x); return y; } void put(pl a){ for(int i=0;i<a.size();i++) printf("%lld ",a[i]); puts(""); } int n,a[N],lm,jc[N],ij[N],m,b[N],k; pl ff(int *a,int l,int r){ if(l==r){ pl c; c.resize(2); c[0]=1; c[1]=(-a[l]+mo)%mo; return c; } return ff(a,l,(l+r)/2)*ff(a,(l+r)/2+1,r); } pl gt(pl x,int n){ pl y,z; y.resize(2); y[1]=1; z.resize(1); z[0]=n; x=x*y; x[0]; x[1]; return z-x; } signed main(){ cin>>n>>m; if(n==1){ if(m==0)puts("1"); else puts("0"); return 0; } jc[0]=ij[0]=1; for(int i=1;i<N;i++) jc[i]=1ll*jc[i-1]*i%mo; ij[N-1]=qp(jc[N-1],mo-2); for(int i=N-1;i;i--) ij[i-1]=1ll*ij[i]*i%mo; int r=1; for(int i=1;i<=n;i++){ cin>>a[i]; r=r*a[i]%mo; } pl b=ff(a,1,n); b=ln(b); b=qd(b); b.push_back((mo-b[n-1])%mo); for(int i=n-1;i;i--) b[i]=(mo-b[i-1])%mo; b[0]=n; pl e,f; e.resize(n+1); f.resize(n+1); for(int i=0;i<=n;i++){ e[i]=qp(i+1,2*m)*ij[i]%mo; f[i]=qp(i+1,m)*ij[i]%mo; } e=e*iv(f); e.resize(n+1); f=ln(f); for(int i=0;i<=n;i++){ e[i]=e[i]*b[i]%mo; f[i]=f[i]*b[i]%mo; } f=ep(f); e=e*f; cout<<e[n-2]*jc[n-2]%mo*r%mo; }
uoj77
这道题可以想到最小割建图。
一个点被分在左边表示选黑色,右边表示选白色。
如果只有区间连边限制的话,可以这样建图:
s->i连w,i->t连b,对于每个i,新建i'->i连p
如果j按题目要求(在一个区间内)可以让i成为奇怪的格子的话,让j向i'连inf边。
这样子如果j选了黑色,那么j,i'要在同一边,要么获得b的代价(选择黑色),要么获得w+p的代价(获得白色和奇怪的代价)
使用线段树优化建边。建立一棵线段树,线段树每个儿子节点向父亲连边。
对于每个i,在线段树上定位出[l[i],r[i]],把这些定位点向i'连边(流量inf),i'向i连边,s向i连边,i向t连边。
对于每个i,在线段树上给叶子连边。流量均为inf
实际上,儿子->父亲连的好处是:儿子的所有流量都可以流向父亲且不被限制,父亲可以连向另外的点,达到了区间连边的限制。
现在有前缀连边的限制,要维护前缀的线段树(可持久化线段树)
把每个新建的点往后面对应的点连边,流量inf。
插入以后查询,向对应的点连边,流量inf。
这样就能解决这道题了。

#include<bits/stdc++.h> using namespace std; #define N 1500010 int h[N],nxt[N],v[N],w[N],s,t,dep[N],ec,n,ct,cc,lc[N],rc[N],rt[N]; void add(int a,int b,int c){v[++ec]=b;w[ec]=c;nxt[ec]=h[a];h[a]=ec;} void adj(int x,int y,int z){add(x,y,z);add(y,x,0);} bool bfs(){ queue<int>q;q.push(s);memset(dep,0,sizeof(dep));dep[s]=1; while(!q.empty()){ int x=q.front();q.pop(); for(int i=h[x];i;i=nxt[i]) if(w[i]>0&&!dep[v[i]]) dep[v[i]]=dep[x]+1,q.push(v[i]); }return dep[t]; } int dfs(int x,int dis){ if(x==t||!dis)return dis;int tp=0; for(int i=h[x];i&&tp<dis;i=nxt[i]) if(dep[v[i]]==dep[x]+1&&w[i]>0){ int f=dfs(v[i],min(dis-tp,w[i])); w[i]-=f;w[i^1]+=f;tp+=f; } if(!tp)dep[x]=0;return tp; } int din(){ int aans=0; while(bfs())aans+=dfs(s,1e9); return aans; } void q(int o,int l,int r,int x,int y){ if(!o||r<x||y<l)return; if(x<=l&&r<=y){ adj(o,cc,1e9); return; } int md=(l+r)/2; q(lc[o],l,md,x,y); q(rc[o],md+1,r,x,y); } void ins(int &o,int p,int l,int r,int x,int y){ o=++ct; lc[o]=lc[p]; rc[o]=rc[p]; if(p)adj(p,o,1e9); adj(y,o,1e9); if(l==r)return; int md=(l+r)/2; x<=md?ins(lc[o],lc[p],l,md,x,y):ins(rc[o],rc[p],md+1,r,x,y); } int main(){ int rr=0; ec=1; cin>>n; s=n*35; t=s+1; ct=n*2; for(int i=1;i<=n;i++){ int u,b,w,l,r,p; cin>>u>>b>>w>>l>>r>>p; rr+=b; rr+=w; cc=i+n; adj(s,i,w); adj(i,t,b); adj(i+n,i,p); q(rt[i-1],0,1000000000,l,r); ins(rt[i],rt[i-1],0,1000000000,u,i); } cout<<rr-din(); }
lg4292
法1:点分。先分数规划,把每个数都减去mid,则问题转化为询问是否有一条路径长度在[l,r]内且权值>=0
寻找过分治重心的路径。把路径按照长度降序排序,枚举一条路径,如果这条路径的边数为j,则另外一条路径的边数要为[l-j,r-j]。这个可以使用单调队列维护。
法2:长剖+线段树。先长剖,再求出长剖序。
长剖序就是每次先dfs长儿子,再dfs短儿子。这样子做的好处是:每一条链都是线段树上的一段连续的节点。
设一棵线段树,上面每一个节点存储的都是:dfs序为x的节点到根的信息。
设f[x][i]表示节点x到儿子的距离为i,根->i的最大权值。
这个可以长链剖分O(n)求出。
在统计答案时,枚举每一条链和对应的长度,假设这个长度为j,则另外一条路径的长度要为[l-j,r-j],可以线段树维护。
在统计完答案时,把现在这个子树(短儿子)合并到线段树中。
注意到上面的f可以在线段树合并贡献时顺便求出来,省掉求f的代码。
代码很好写。

#include<bits/stdc++.h> #define db double #define N 400010 #define int long long using namespace std; int h[N],v[N],nxt[N],ec,id[N],dd[N],ct,p[N],n,l,u,x,y,z,d[N],po[N]; db mx[N],w[N],aa,dp[N],va[N]; void add(int x,int y,int z){v[++ec]=y;w[ec]=z;nxt[ec]=h[x];h[x]=ec;} void bd(int o,int l,int r){ mx[o]=-1e18; if(l==r)return; int md=(l+r)/2; bd(o*2,l,md); bd(o*2+1,md+1,r); } db q(int o,int l,int r,int x,int y){ if(r<x||y<l)return -1e18; if(x<=l&&r<=y)return mx[o]; int md=(l+r)/2; return max(q(o*2,l,md,x,y),q(o*2+1,md+1,r,x,y)); } void mod(int o,int l,int r,int x,db y){ mx[o]=max(mx[o],y); if(l==r)return; int md=(l+r)/2; x<=md?mod(o*2,l,md,x,y):mod(o*2+1,md+1,r,x,y); } void d1(int x,int fa){ for(int i=h[x];i;i=nxt[i]) if(v[i]!=fa){ d1(v[i],x); if(dd[v[i]]>dd[p[x]])p[x]=v[i]; } dd[x]=dd[p[x]]+1; } void d2(int x,int fa){ po[x]=++ct; if(p[x])d2(p[x],x); for(int i=h[x];i;i=nxt[i]) if(v[i]!=fa&&v[i]!=p[x]) d2(v[i],x); } void d3(int x,int fa){ mod(1,1,n,po[x],dp[x]); for(int i=h[x];i;i=nxt[i]) if(v[i]==p[x]){ dp[v[i]]=dp[x]+w[i]; d3(v[i],x); } for(int i=h[x];i;i=nxt[i]) if(v[i]!=fa&&v[i]!=p[x]){ dp[v[i]]=dp[x]+w[i]; d3(v[i],x); for(int j=1;j<=dd[v[i]];j++){ va[j]=q(1,1,n,po[v[i]]+j-1,po[v[i]]+j-1); aa=max(aa,q(1,1,n,max(po[x],po[x]+l-j),min(n,min(po[x]+u-j,po[x]+dd[x]-1)))+va[j]-2*dp[x]); } for(int j=1;j<=dd[v[i]];j++) mod(1,1,n,po[x]+j,va[j]); } aa=max(aa,q(1,1,n,po[x]+l,min(n,min(po[x]+u,po[x]+dd[x]-1)))-dp[x]); } signed main(){ cin>>n>>l>>u; for(int i=1;i<n;i++){ scanf("%lld%lld%lld",&x,&y,&z); add(x,y,z); add(y,x,z); } d1(1,0); d2(1,0); db l=0,r=1e6; while(l+1e-5<r){ db md=(l+r)/2; for(int i=1;i<=ec;i++) w[i]-=md; bd(1,1,n); aa=-1e18; d3(1,0); if(aa<0)r=md; else l=md; for(int i=1;i<=ec;i++) w[i]+=md; } printf("%.3lf ",l); }
lg6515
以后要多做计算几何和线性代数的题目。
发现一个(a,b)当一维为负时,无论怎么操作都不能使两维同时变正。
这道题可以把一对(a,b)视为向量,则变换都是在向量上乘以一个矩阵。
实际上,现在的(a,b)可以被表示成(ax+by,cx+dy)(x,y为原向量)。
如果向量在"合法平面"上,则这个向量还是可以被操作的。
所以过程未结束的条件可以被写成向量在"合法平面"上。
每次1操作相当于把平面在下面的部分砍掉一些。操作2相当于打个标记,在下面一次操作(一定是1操作)把平面砍掉一些。
把所有向量按极角从小到大排序,则结束条件可以被写成:"合法平面"在排序后数组位置相邻2个点之间。
枚举每一对相邻的向量。分3种情况讨论:
1.当前向量两个都在y=x下面。用1操作会砍掉y=x下面的平面,这两个向量也会被砍掉。所以只能用2操作。
2.当前向量两个都在y=x上面,只能用1操作。若进行2操作,则反转后会变成1情况,只能继续用2操作。
3.当前向量一个在y=x下面,一个在上面。只要进行操作1,下面的向量就不可操作。
这时不应该继续进行操作1。如果继续进行操作1,可以对称后再进行操作1。如果未对称后继续砍平面,则不能让合法平面上砍掉上面的向量。这样子不符合要求。
所以应该对称后再砍。
实际上,一开始也可能对称,这样子可能步数更小。所以需要比较两种方法的优劣,再决定怎么操作。
时间复杂度:情况1会转变成情况2,但是情况2会持续很多次。这是瓶颈。
所以可以使用除法算出2要进行的次数。
时间复杂度分析同辗转相除。
lg3789
略

#include<bits/stdc++.h> using namespace std; #define mo 998244353 #define N 5000010 #define ll unsigned long long #define int long long #define pl vector<int> int qp(int x,int y){ int r=1; for(;y;y>>=1,x=1ll*x*x%mo) if(y&1)r=1ll*r*x%mo; return r; } int m,rev[N],v,le,w[N],p[N]; int n,a[N],lm,jc[N],ij[N],ml,k,g[N]; void deb(pl x){ for(int i:x)cout<<i<<' '; puts(""); } void init(int n){ v=1; le=0; while(v<n)le++,v*=2; for(int i=0;i<v;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(le-1)); int g=qp(3,(mo-1)/v); w[v/2]=1; for(int i=v/2+1;i<v;i++) w[i]=1ull*w[i-1]*g%mo; for(int i=v/2-1;~i;i--) w[i]=w[i*2]; } void fft(int v,pl &a,int t){ static unsigned long long b[N]; int s=le-__builtin_ctz(v); for(int i=0;i<v;i++) b[rev[i]>>s]=a[i]; int c=0; w[0]=1; for(int i=1;i<v;i*=2,c++) for(int r=i*2,j=0;j<v;j+=r) for(int k=0;k<i;k++){ int tx=b[j+i+k]*w[k+i]%mo; b[j+i+k]=b[j+k]+mo-tx; b[j+k]+=tx; } for(int i=0;i<v;i++) a[i]=b[i]%mo; if(t==0)return; int iv=qp(v,mo-2); for(int i=0;i<v;i++) a[i]=1ull*a[i]*iv%mo; a.resize(v); reverse(a.begin()+1,a.end()); } pl operator *(pl x,pl y){ int s=x.size()+y.size()-1; if(x.size()<=20||y.size()<=20){ pl r; r.resize(s); for(int i=0;i<x.size();i++) for(int j=0;j<y.size();j++) r[i+j]=(r[i+j]+x[i]*y[j])%mo; r.resize(k+1); return r; } init(s); x.resize(v); y.resize(v); fft(v,x,0); fft(v,y,0); //deb(x); //deb(y); for(int i=0;i<v;i++) x[i]=x[i]*y[i]%mo; fft(v,x,1); x.resize(s); return x; } void inv(int n,pl &b,pl &a){ if(n==1){ b[0]=qp(a[0],mo-2); return; } inv((n+1)/2,b,a); static pl c; init(n*2); c.resize(v); b.resize(v); for(int i=0;i<n;i++) c[i]=a[i]; fft(v,c,0); //deb(c); fft(v,b,0); //deb(b); for(int i=0;i<v;i++) b[i]=1ll*(2ll-1ll*c[i]*b[i]%mo+mo)%mo*b[i]%mo; //deb(b); fft(v,b,1); b.resize(n); //deb(b); } void ad(pl &x,pl y,int l){ x.resize(max((int)x.size(),(int)y.size()+l)); for(int i=0;i<y.size();i++) x[i+l]=(x[i+l]+y[i])%mo; } pl operator +(pl x,pl y){ ad(x,y,0); return x; } pl iv(pl x){ pl y; int n=x.size(); y.resize(n); inv(n,y,x); y.resize(n); return y; } pl operator /(pl a,pl y){ int n=a.size()-1,m=y.size()-1; pl x,b,t; x.resize(n+1); b.resize(m+1); for(int i=0;i<=n;i++) x[n-i]=a[i]; for(int i=0;i<=m;i++) b[m-i]=y[i]; for(int i=n-m+2;i<=m;i++) b[i]=0; b.resize(n-m+1); t=iv(b); //deb(t); //deb(x); //deb(t); x=x*t; //deb(x); x.resize(n-m+1); reverse(x.begin(),x.end()); return x; } void sq(int n,pl &b,pl &a){ if(n==1){ b[0]=3; return; } sq((n+1)/2,b,a); pl c,d=a; int ii=qp(2,mo-2); c.resize(n); b.resize(n); d.resize(n); for(int i=0;i<b.size();i++) c[i]=1ll*b[i]*ii%mo; for(int i=0;i<b.size();i++) b[i]=1ll*b[i]*2%mo; d=d*iv(b); for(int i=0;i<b.size();i++) b[i]=(c[i]+d[i])%mo; } pl sq(pl x){ pl y; int n=x.size(); y.resize(n); sq(n,y,x); y.resize(n); return y; } pl operator -(pl x,pl y){ int s=max(x.size(),y.size()); x.resize(s); y.resize(s); for(int i=0;i<s;i++) x[i]=(x[i]-y[i]+mo)%mo; return x; } pl operator %(pl x,pl y){ int n=(int)x.size()-1,m=(int)y.size()-1; if(x.size()<y.size())return x; if(!m){ pl a; a.resize(1); return a; } x=x-(x/y)*y; x.resize(m); return x; } pl qd(pl x){ pl y; int n=x.size(); y.resize(n-1); //deb(x); for(int i=0;i<n-1;i++) y[i]=x[i+1]*(i+1)%mo; //deb(y); return y; } pl jf(pl x){ int n=x.size(); pl y; y.resize(n+1); for(int i=1;i<=n;i++) y[i]=x[i-1]*qp(i,mo-2)%mo; return y; } pl ln(pl x){ int n=x.size(); pl y=qd(x),z=iv(x); y=y*z; y=jf(y); y.resize(n); return y; } inline char nc(){ static char buf[500000],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,500000,stdin),p1==p2)?EOF:*p1++; } inline int rd(){ char ch=nc();int sum=0; while(!(ch>='0'&&ch<='9'))ch=nc(); while(ch>='0'&&ch<='9')sum=sum*10+ch-48,ch=nc(); return sum; } char bf[100]; void wr(int x){ if(!x){ putchar('0'); putchar(' '); return; } int ct=0; while(x){ bf[++ct]=x%10; x/=10; } for(int i=ct;i;i--) putchar(bf[i]+'0'); putchar(' '); } namespace qz{ ll b[N],ans[N],pp[N]; pl t; void fz(int o,int l,int r,pl &p,pl *a){ if(l==r){ a[o].resize(2); a[o][0]=(mo-p[l])%mo; a[o][1]=1; return; } int md=(l+r)/2; fz(o*2,l,md,p,a); fz(o*2+1,md+1,r,p,a); a[o]=a[o*2]*a[o*2+1]; //deb(a[o]); } void ga(int o,int l,int r,pl &ans,pl *a,pl *c){ if(r-l<=100){ for(int i=l;i<=r;i++){ int r=0; for(int j=c[o].size()-1;~j;j--) r=(1ll*r*pp[i]%mo+c[o][j])%mo; ans[i]=r; } return; } if(l==r){ ans[l]=c[o][0]; return; } int md=(l+r)/2; c[o*2]=c[o]%a[o*2]; c[o*2+1]=c[o]%a[o*2+1]; ga(o*2,l,md,ans,a,c); ga(o*2+1,md+1,r,ans,a,c); } void gt(pl t,pl &ans){ //while(t.size()<ans.size())t.push_back(0); int n=ans.size(); static pl a[N],b[N]; for(int i=0;i<n;i++) pp[i]=ans[i]; fz(1,0,n-1,ans,a); if(n>=m)b[1]=t%a[1]; ga(1,0,n-1,ans,a,b); } void d2(int o,int l,int r,pl &y,pl *a,pl *b){ if(l==r){ b[o].resize(1); b[o][0]=y[l]; return; } int md=(l+r)/2; d2(o*2,l,md,y,a,b); d2(o*2+1,md+1,r,y,a,b); b[o]=b[o*2]*a[o*2+1]+b[o*2+1]*a[o*2]; } }; pl cz(int n,pl &x,pl &y){ static pl a[N],b[N]; qz::fz(1,0,n-1,x,a); qz::gt(qd(a[1]),x); //deb(x); for(int i=0;i<n;i++) y[i]=y[i]*qp(x[i],mo-2)%mo; //deb(y); qz::d2(1,0,n-1,y,a,b); return b[1]; } void gt(int n,pl &y,pl x){ if(n==1){ y.resize(1); y[0]=1; return; } gt((n+1)/2,y,x); pl z=x,a; z.resize(n); y.resize(n); a.resize(1); a[0]=1; y=y*(a-ln(y)+z); y.resize(n); } pl ep(pl x){ pl y; int n=x.size(); gt(n,y,x); return y; } pl qp(pl x,int y){ int iv=qp(x[0],mo-2),t=x[0]; for(int i=0;i<x.size();i++) x[i]=x[i]*iv%mo; pl r=ln(x); for(int i=0;i<r.size();i++) r[i]=r[i]*(y%mo)%mo; r=ep(r); for(int i=0;i<r.size();i++) r[i]=r[i]*qp(t,y%(mo-1))%mo; return r; } void put(pl a){ for(int i=0;i<a.size();i++) printf("%lld ",a[i]); puts(""); } signed main(){ freopen("w1.out","w",stdout); cin>>n>>k; pl ss,t,tt; ss.resize(k+1); ss[0]=9; ss[1]=mo-2; ss[2]=1; ss=sq(ss); tt=iv(ss); pl v1=ss,v2=t-ss; v1[0]=(v1[0]+1)%mo; v1[1]=(v1[1]+1)%mo; v2[0]=(v2[0]+1)%mo; v2[1]=(v2[1]+1)%mo; for(int i=0;i<=k;i++){ v1[i]=qp(2,mo-2)*v1[i]%mo; v2[i]=qp(2,mo-2)*v2[i]%mo; } pl v3=qp(v1,n-1),v4=qp(v2,n-1),v5,v6; v5=v3-v4; v3=v3*v1; v4=v4*v2; v6=v3-v4; v5=v5*tt; v6=v6*tt; for(int i=0;i<=k;i++) g[i]=(v6[i]+v5[i]*2)%mo; for(int i=1;i<=k;i++) g[i]=(g[i]-v5[i-1]+mo)%mo; for(int i=0;i<=k;i++) cout<<(g[i]+v6[i]*2)%mo<<' '; }
lg5243
这道题是个dp。
这道题构成欧拉回路的条件也可以被写成:从每棵树上选出一条路径,且路径的长度之和>=y
设f[i][0]表示当前的树的方案数,f[i][1]表示当前的树的方案数的长度和。
则f[i+j][0]=f[i][0]+f[j][0]
f[i+j][1]=f[i][0]*f[j][1]+f[j][0]+f[i][1]
题目上限制的路径长度之和>=y要求我们不能把路径的长度具体的在状态上存起来,有2种处理方法:
1.容斥:变成<y
2.在dp的时候,把第一维对y取min,最后取y这一维作为答案即可。
加一个剪枝即可过此题。
uoj94
集合幂级数的一道入门题。
fwt的几条重要性质:它的直接定义式可以考虑变换的过程求出。它是线性变换(和的fwt=fwt的和)。fwt的逆变换要乘的矩阵就是原变换矩阵的逆矩阵。如果要乘法,则可以fwt后点乘。
定义子集卷积:f[s|t]+=a[s]*b[t](s&t==0)
这样子直接做是O(3^n)的
但是可以使用占位多项式优化。
设f[i][s],f[i][s]只有当i=bitcount(s)时为a[s],否则为0
f[x+y][]+=a[x][]*b[y][]
如果设s的1位数位x,t的为y
则x+y=bitcount(s|t)等价于s&t=0
所以可以对f[i][]作高维前缀和(原因后面再讲),再进行点乘。
这样子时间复杂度是2^n*n^2的
实际上,发现f[][j],每一个j在做完后是独立的,f[i][]构成了2^n个多项式。
这带给了一些优美的性质。
f[][j]的求逆可在2^n*n^2的时间复杂度内完成,对每个多项式求逆即可。
定义幂级数的导数为$x^S=bitcount(s)x^{s-{t}}$t为任意集合。
发现这个导数的定义满足导数的性质。但是定义积分是困难的。
只要作高维前缀和,就可以快速计算导数(就是占位多项式的前一位),同时推出集合幂级数求ln的做法。
回到原题。设g表示原图的连通生成子图的集合幂级数。h表示导出子图的个数的集合幂级数。
有h+1=sum g^k/k!(k>1)=e^g
ln(h+1)=g
最后要求的:sum i>0 g^k =1/(1-g)(内部的系数已经带入函数了)
把ln带进,得1/(1-ln(h+1))
ln就是对占位多项式求ln。时间复杂度2^n*n^2

#include<bits/stdc++.h> using namespace std; #define N 21 #define mo 998244353 int n,m,f[N][(1<<20)+10],g[N][(1<<20)+10],c[(1<<20)+10],iv[N],a[N*N],b[N*N]; void fwor(int *a,int l,int r){ if(l==r)return; int md=(l+r)/2; fwor(a,l,md);fwor(a,md+1,r); for(int i=l;i<=md;i++) a[md+i-l+1]=(a[md+i-l+1]+a[i])%mo; } void ifwor(int *a,int l,int r){ if(l==r)return; int md=(l+r)/2; ifwor(a,l,md);ifwor(a,md+1,r); for(int i=l;i<=md;i++) a[md+i-l+1]=(a[md+i-l+1]-a[i]+mo)%mo; } int qp(int x,int y){ int r=1; for(;y;y>>=1,x=1ll*x*x%mo) if(y&1)r=1ll*r*x%mo; return r; } signed main(){ cin>>n>>m; for(int i=0;i<m;i++){ cin>>a[i]>>b[i]; a[i]--; b[i]--; } for(int i=1;i<(1<<n);i++){ c[i]=c[i>>1]+(i&1); int ct=0; for(int j=0;j<m;j++) if((i&(1<<a[j]))&&(i&(1<<b[j])))ct++; f[c[i]][i]=qp(2,ct); } for(int i=1;i<=n;i++){ fwor(f[i],0,(1<<n)-1); iv[i]=qp(i,mo-2); } for(int i=1;i<=n;i++){ for(int k=0;k<i;k++) for(int j=0;j<(1<<n);j++) g[i][j]=(g[i][j]+1ll*k*g[k][j]%mo*f[i-k][j])%mo; for(int j=0;j<(1<<n);j++) g[i][j]=(f[i][j]+1ll*(mo-iv[i])*g[i][j]%mo)%mo; } memset(f,0,sizeof(f)); for(int i=0;i<(1<<n);i++) f[0][i]=1; for(int i=1;i<=n;i++) for(int k=0;k<i;k++) for(int j=0;j<(1<<n);j++) f[i][j]=(f[i][j]+1ll*f[k][j]*g[i-k][j]%mo)%mo; ifwor(f[n],0,(1<<n)-1); cout<<f[n][(1<<n)-1]; }
uoj310
略

#include<bits/stdc++.h> using namespace std; #define N 4000010 #define mo 998244353 #define int long long int n,c[N],x,mx,v,le,p3[N],r; void fwxo(int *a,int l,int r){ if(l==r)return; int md=(l+r)/2; fwxo(a,l,md);fwxo(a,md+1,r); for(int i=l;i<=md;i++){ int c=a[i],d=a[md+i-l+1]; a[md+i-l+1]=c-d; a[i]=c+d; } } int qp(int x,int y){ int r=1; for(;y;y>>=1,x=x*x%mo) if(y&1)r=r*x%mo; return r; } signed main(){ cin>>n; for(int i=1;i<=n;i++){ scanf("%lld",&x); c[x]++; mx=max(mx,x); } p3[0]=1; for(int i=1;i<N;i++) p3[i]=p3[i-1]*(mo-3)%mo; v=1; while(v<mx)v*=2,le++; fwxo(c,0,v-1); for(int i=0;i<v;i++) r=(r+p3[(c[i]+n)/2])%mo; r=r*qp((mo+1)/2,le)%mo; if(n&1)r=(mo-r)%mo; r=(r-1+mo)%mo; cout<<r; }
