这道题实际上是个背包问题。
设f[i][j]表示扔i次骰子,总点数为j的概率。
f[i][j]=sum f[i-1][j-k]*1/n
这个dp可以使用生成函数优化。
构造生成函数f(x)=1/n (1+x+...+x^(n-1))
表示扔到0~n-1的概率
这道题就是让求f(x)^m的a~b系数。
如果g(x)=f(x)的前缀和,则就是让求g(x)[x^b]-g(x)[x^(a-1)]
直接这样做要多项式求快速幂。
但是实际上多项式的乘法就是点值的乘法,可以直接把长度设成>=x*y对点值快速幂。
这样子是xylogxy的,由于loj机子神速可以通过。
正解对小的部分进行多项式乘法,大的用中心极限定理。
设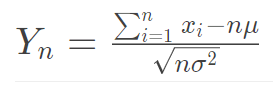
其中x为每次扔出的点,期望为μ,方差为σ^2
则当n足够大的时候,上面的式子服从标准正态分布N(0,1)
在原题中,a<=x的和<=b
那么把和带入标准正态分布的公式内,得到
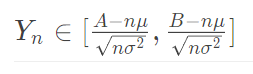
自适应辛普森法就是对一个区间使用二次函数拟合,使用公式
$frac{(r-l)(f(l)+4f(md)+f(r))}{6}$
拟合。这个可以假设函数是个二次函数,然后计算得来。
在自适应辛普森法中,假设现在(l,r)区间算出的结果为x,左边(l,md)算出的结果为a,右边的为b
若abs(x-a-b)<eps,则接下来的改进幅度不大,所以不用继续递归。否则递归到下面的区间计算答案。
还有模意义下的做法。
继续对生成函数进行推导,我们要对f(x)^m求前缀和,为了求前缀和要乘以(1+x+x^2+....)再推导。
设g为f的前缀和,则
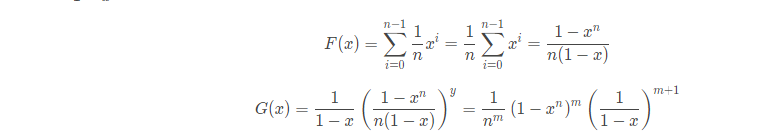
把g展开,得到
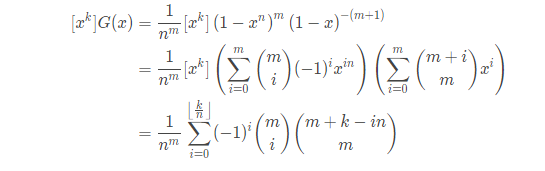
后面的负系数的展开意义是:i个球放到m个盒子里,盒子可以为空。
把每个盒子多放一个球就变成了经典组合问题。