▶ 图片参考【http://www.bu.edu/pasi/files/2011/01/NathanBell1-10-1000.pdf】
▶ 各种系数矩阵的数据结构
● MAT,原始矩阵数据
1 typedef struct // 顺序格式 2 { 3 int row; // 行数 4 int col; // 列数 5 int count; // 非零元个数(用于转换,不用于计算) 6 format *data; // 元素的值 7 } 8 MAT;
● Compressed Sparse Row(CSR),由非零值向量,各元素列号向量,各行首元在列号向量中的起始位置向量组成
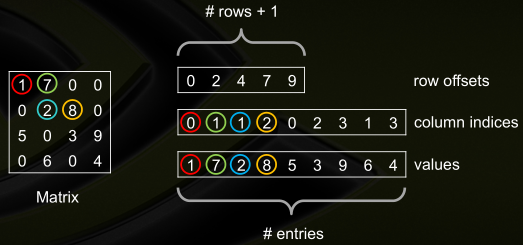
1 typedef struct 2 { 3 int row; // 行数 4 int col; // 列数 5 format *data; // 非零元的值 6 int *index; // 非零元的列号 7 int *ptr; // 每行首元在 index 中的下标,最后一个元素的值等于矩阵非零元个数 8 } 9 CSR;
● Compressed Sparse Column Format (CSC),类似 CSR,不过是列优先存储,实现暂时没写,留坑

1 typedef struct 2 { 3 int row; // 行数 4 int col; // 列数 5 format *data; // 非零元的值 6 int *index; // 非零元的行号 7 int *ptr; // 每列首元在 index 中的下标,最后一个元素的值等于矩阵非零元个数 8 } 9 CSC;
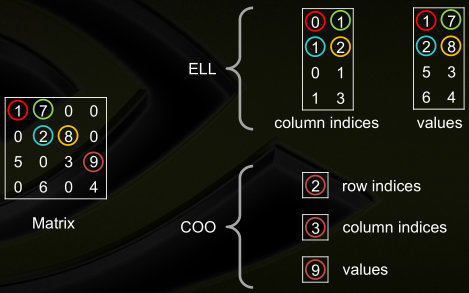
● ELLPACK(ELL),记录非零元的列号,然后把非零元素压缩到最左边。为了提高内存读取,我的 ELL 相当于将图中的两个矩阵进行了转置

1 typedef struct 2 { 3 int row; // 行数,等于 MAT 格式非零元最多行的非零元个数 4 int col; // 列数,等于 MAT 格式的行数 5 int colOrigin; // 原列数,等于 MAT 格式的列数 6 format *data; // 非零元的值 7 int *index; // 元素在原矩阵中的列号 8 } 9 ELL;
● Coordinate(COO),用行列坐标来记录每个非零元的位置

1 typedef struct 2 { 3 int row; // 行数 4 int col; // 列数 5 int count; // 非零元个数 6 int *rowIndex; // 行向量 7 int *colIndex; // 列向量 8 format *data; // 元素的值 9 } 10 COO;
● Diagonal(DIA),相当于将矩阵的主对角线捋成一列,其他元素水平移动,然后砍掉所有元素均为零的列(即原矩阵中所有元素均为零的对角线),变换后矩阵行数不变,列数可能增大或减小
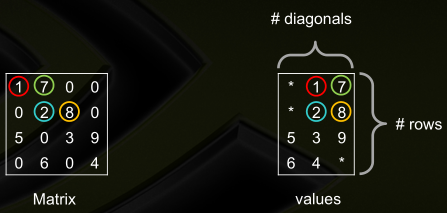
1 typedef struct 2 { 3 int row; // 行数 4 int col; // 列数 5 int colOrigin; // 原列数 6 format *data; // 元素的值 7 int *index; // 原矩阵各对角线是否非零 8 } 9 DIA;
● Hybrid (HYB) ELL + COO,相当于先尽量 ELL,右边多出的部分砍下来用 COO 单独保存。实现暂时没写,留坑
● Skyline Matrix Storage Format,参考【https://software.intel.com/en-us/mkl-developer-reference-c-sparse-blas-skyline-matrix-storage-format】。实现暂时没写,留坑
■ 例如,下三角中,value 按行优先保存了主对角线及其左下部的元素,每行开头的零略掉但中间的零不省略,ptr 记录每行第一个非零元在 value 中的下标;上三角类似,但是按列优先排列元素。

● Block Sparse Row(BSR),参考【https://software.intel.com/en-us/mkl-developer-reference-c-sparse-blas-bsr-matrix-storage-format】,那个 4 向量的版本没太理解,3 向量的版本参考【http://www.cs.colostate.edu/~mcrob/toolbox/c+/sparse_matrix_compression.html】看懂了。实现暂时没写,留坑
■ 3 向量版本中,value 表示分块小矩阵的值,呈行优先排列,小矩阵元素展开成一维时内部要列优先排列(这里超出了 Mathtype 的最大宽度,所以没有展开),col_index 表示每个小矩阵起始列号,row_ptr 表示每行首个非零小矩阵在 col_index 中的下标
