Yolo-V4算法中对网络进行了改进,使用CSPDarknet53。网络结构如下:

Yolo-V4与Yolo-V3上相比较:
(1)对主干网络进行了修改,将原先的Darknet53改为CSPDarknet53,其中是将激活函数改为Mish激活函数,并且在网络中加入了CSP结构。
(2)对特征提取过程的加强,添加了SPP,PANet结构。
(3)在数据预处理阶段加入Mosaic方法。
(4)在损失函数中做了改进使用了CIOU作为回归Loss。
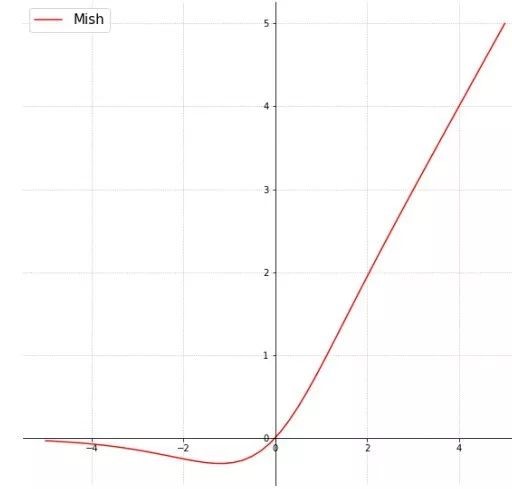
Mish激活函数:
Mish() = x×tanh(ln(1+ex)),使用Mish函数可以对负值有更好的梯度流,而不是像ReLU函数中那样的全零。这样平滑的激活函数允许更好的信息深入神经网络,从而得到更好的准确信息。
CSPNet结构:
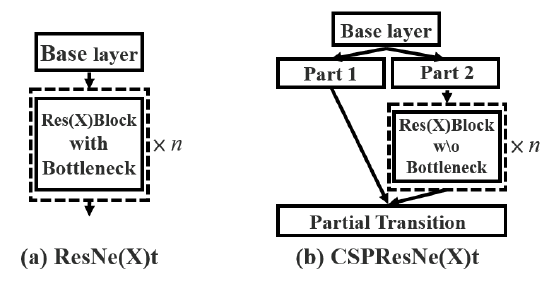
CSP是可以增强CNN学习能力的新型结构,CSPNet将底层的特征映射分为两部分,一部分经过密集块和过渡层,另一部分与传输的特征映射结合到下一阶段。
from functools import wraps from keras import backend as K from keras.layers import Conv2D,Add,ZeroPadding2D,UpSampling2D,Concatenate,MaxPooling2D,Layer,Input from keras.layers.advanced_activations import LeakyReLU from keras.layers.normalization import BatchNormalization from keras.regularizers import l2 from keras.layers import Activation from keras import Model #将定义好的函数添加到keras系统中 from keras.utils import get_custom_objects # class Mish(Activation): # def __init__(self,activation): # super(Mish, self).__init__(activation) # self.__name__ ="Mish" # def mish(inputs): # return inputs*K.tanh(K.softplus(inputs)) # get_custom_objects().update({"Mish":Mish(mish)}) class Mish(Layer): def __init__(self): super(Mish, self).__init__() def call(self,inputs): return inputs * K.tanh(K.softplus(inputs)) #darknet单次卷积 def DarknetConv2D(*args,**kwargs): darknet_conv_kwargs = {"kernel_regularizer":l2(5e-4)} darknet_conv_kwargs["padding"]="valid" if kwargs.get("strides")==(2,2) else "same" darknet_conv_kwargs.update(kwargs) return Conv2D(*args,**darknet_conv_kwargs) #卷积块 def DarknetConv2D_BN_Mish(x,*args,**kwargs): no_bias_kwargs={"use_bias":False} no_bias_kwargs.update(kwargs) x=DarknetConv2D(*args,**no_bias_kwargs)(x) x=BatchNormalization()(x) #x=Activation("Mish")(x) x=Mish()(x) return x def DarknetConv2D_BN_Leaky(x, *args, **kwargs): no_bias_kwargs = {"use_bias": False} no_bias_kwargs.update(kwargs) x = DarknetConv2D(*args, **no_bias_kwargs)(x) x = BatchNormalization()(x) # x=Activation("Mish")(x) x = LeakyReLU(alpha=0.1)(x) return x def resblock_body(x,num_filters,num_blocks,all_narrow=True): preconv1 =ZeroPadding2D(padding=((1,0),(1,0)))(x) preconv1 =DarknetConv2D_BN_Mish(preconv1,num_filters,(3,3),strides=(2,2)) #生成一个大的残差边 shortconv =DarknetConv2D_BN_Mish(preconv1,num_filters//2 if all_narrow else num_filters,(1,1)) #主干部分的卷积 mainconv =DarknetConv2D_BN_Mish(preconv1,num_filters//2 if all_narrow else num_filters,(1,1)) for i in range(num_blocks): x=DarknetConv2D_BN_Mish(mainconv,num_filters//2,(1,1)) x=DarknetConv2D_BN_Mish(x,num_filters//2 if all_narrow else num_filters,(3,3)) mainconv=Add()([mainconv,x]) postconv =DarknetConv2D_BN_Mish(mainconv,num_filters//2 if all_narrow else num_filters,(1,1)) route = Concatenate()([postconv,shortconv]) return DarknetConv2D_BN_Mish(route,num_filters,(1,1)) def darknet_body(x): x =DarknetConv2D_BN_Mish(x,32,(3,3)) x=resblock_body(x,64,1,False) x=resblock_body(x,128,2) x=resblock_body(x,256,8) feat1=x x=resblock_body(x,512,8) feat2=x x=resblock_body(x,1024,4) feat3=x return feat1,feat2,feat3
Mosaic数据增强:
(1)每次读取四张图片
(2)分别对这四张图片进行翻转,缩放,色域变化等,并且按照四个方向位置摆好。
(3)进行图片的组合和框的组合。
Label Smoothing-防止过拟合:
在分类模型当中,经常对标签使用one-hot的形式,然后去预测属于每一个标签的概率,如果不考虑多标签的情况下,选择概率最大的作为我们的预测标签。但是在实际过程中可能会存在两个问题。
(1)可能导致过拟合。
(2)模型对于预测过于自信,以至于忽略可能的小样本标签。
产生上述问题的原因就是因为我们真正在计算交叉熵损失函数的时候,对于真实标签概率的取值要么是1,要么是0,表征我们已知样本属于某一类别的概率是为1的确定事件,属于其他类别的概率则均为0。Label Smoothing的原理就是为损失函数增强其他标签的损失函数值,类似于其为非标签增加了一定的可选择性。
注:如果分类准确,也就是说交叉熵对分类正确给的是最大激励,但实际上有一些标注数据并不一定是准确的。所以使用上述标签并不一定是最优的。
Label Smoothing:标签×(1-ξ)+ξ/标签个数×[1,1,...1]
def Label_Smoothing(y_true,label_smoothing): y_true = np.cast(y_true,tf.float32) num_classes = float((y_true.shape[-1])) label_smoothing = K.constant(label_smoothing,dtype=K.floatx()) return y_true * (1.0-label_smoothing) + label_smoothing/num_classes
Loss函数:
Loss-IOU
使用Loss-IOU可能会产生梯度消失,因为当BBOX和真实框无交集的时候,这时候Loss-IOU始终为1。反向传播的时候梯度就为0了,产生了梯度消失。Loss-IOU=1-|B∩Bgt|/|B∪Bgt|
Loss-IOU会产生以下几点问题:
(1)如果两个框没有相交,则IOU=0,这是无法反映两个框的距离,并且损失函数此时不存在梯度,无法通过梯度下降训练。
(2)即使相同的IOU也不能代表检测框的定位效果相同。
Loss-GIOU
Loss-GIOU=1-IOU+|c-B∪Bgt|/|c|,与IOU相比,GIOU不仅关注重叠区域,当B和Bgt相对于彼此没有很好的对准时,封闭形状c中的两个对称形状B和Bgt之间的空白空间增加,因此,GIOU的值可以更好的反映两个对称物体之间如何发生重叠,GIOU在两者无交集且无限远的时候是取最小值-1,因此GIOU是一个非常好的距离度量指标。
IOU和GIOU没有考虑到真实框与预测中心之间的距离。实际情况下,中心点的距离越小框预测的越准。GIOU在水平和垂直方向误差很大也就是包含关系。
Loss-DIOU
Loss-DIOU = 1-IOU+δ2(b,bgt)/c2,在Loss-DIOU中,b,bgt分别代表了anchor框和目标框的中心点,且δ代表的是计算两个中心点间的欧式距离,c代表的是能够同时覆盖anchor和目标框的最小矩形的对角线的距离。
(1)DIOU在与目标框不重叠时,仍然可以为边界框提供移动方向。
(2)Loss-DIOU可以直接最小化两个目标的距离,因此比Loss-GIOU收敛的块。
(3)对于包含两个框的水平方向和垂直方向上这种情况,Loss-DIOU可以回归的非常快。
Loss-CIOU
Loss-CIOU=1-IOU+δ(b,bgt)/c2+αV,V=4/Π2[arctan(wgt/hgt)-arctan(w/h)]2,α=V/(1-IOU)+V,从α参数来看,损失函数会更加倾向于往重叠的区域增多方向优化。
#b1预测框,b2真实框 def box_ciou(b1,b2): b1_xy = b1[...,:2] b1_wh = b1[...,2:4] b1_wh_half = b1_wh/2. b1_mins = b1_xy-b1_wh_half b1_maxes = b1_xy+b1_wh_half b2_xy = b2[...,:2] b2_wh = b2[...,2:4] b2_wh_half = b2_wh/2.0 b2_mins = b2_xy-b2_wh_half b2_maxes = b2_xy+b2_wh_half intersect_mins = K.maximum(b1_mins,b2_mins) intersect_maxes = K.minimum(b1_maxes,b2_maxes) intersect_wh = K.maximum(intersect_maxes-intersect_mins,0.) intersect_area = intersect_wh[...,0]*intersect_wh[...,1] b1_area = b1_wh[...,0]*b1_wh[...,1] b2_area = b2_wh[...,0]*b2_wh[...,1] union_area = b1_area+b2_area-intersect_area #K.epsilon()返回一个浮点数 iou = intersect_area/(union_area+K.epsilon()) #计算中心距离 center_distance = K.sum(K.square(b1_xy-b2_xy),axis=-1) #找到包裹两个框的最小框的左上角跟右下角 enclose_mins = K.minimum(b1_mins,b2_mins) enclose_maxes = K.maximum(b1_maxes,b2_maxes) enclose_wh = K.maximum(enclose_maxes-enclose_mins,0.0) #计算对角线距离 enclose_diagonal = K.sum(K.square(enclose_wh),axis=-1) ciou = iou - 1.0 *(center_distance)/(enclose_diagonal+K.epsilon()) v = 4*K.square(tf.math.atan2(b1_wh[...,0],b1_wh[...,1])-tf.math.atan2(b2_wh[...,0],b2_wh[...,1]))/(math.pi*math.pi) alpha = v/(1.0-iou+v) ciou = ciou-alpha*v ciou = K.expand_dims(ciou,axis=-1) return ciou def get_loss_con(ytrue,ypre,noobj_scale,object_mask,IOU): object_mask = K.squeeze(object_mask,axis=-1) con_delta = object_mask*(ypre*IOU-ytrue) + noobj_scale*(1-object_mask)*(ypre*IOU-ytrue) loss_con = K.sum(K.square(con_delta),list(range(1,4))) return loss_con
其他的代码跟V3一样。
模拟余弦退火(学习率):
ηt = ηimin + 1/2(ηimax-ηimin) (1-cos(Tcur/Ti)Π),ηimax和ηimin是学习率的范围,Tcur是随着iteration变化的,Ti是当前run总共的epoch数目。余弦退火衰减算法,学习率会先上升再下降,上升的时候使用线性上升,下降的时候模拟cos函数下降。Tcur/Ti =iteration/TotalIterations。
import numpy as np import matplotlib.pyplot as plt def compute_eta_t(eta_min, eta_max, T_cur, Ti): pi = np.pi eta_t = eta_min + 0.5 * (eta_max - eta_min) * (np.cos(pi * T_cur / Ti) + 1) return eta_t # 每Ti个epoch进行一次restart。 Ti = [20, 40, 80, 160] n_batches = 200 eta_ts = [] for ti in Ti: T_cur = np.arange(0, ti, 1 / n_batches) for t_cur in T_cur: eta_ts.append(compute_eta_t(0, 1, t_cur, ti)) n_iterations = sum(Ti) * n_batches epoch = np.arange(0, n_iterations) / n_batches plt.plot(epoch, eta_ts) plt.show()