zz:https://blog.csdn.net/dreaming__ldx/article/details/81106748
对于样例2
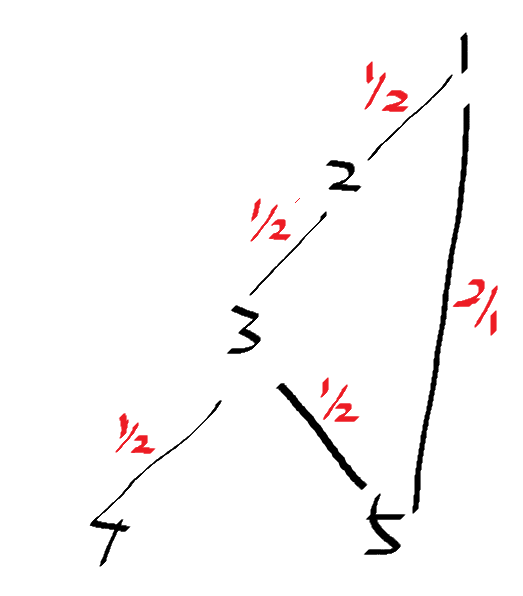
day 出发点 水位 ans
1 5 1 0
2 5 2 2
3 4 2 3
4 2 3 1
以海拔为第一关键字对边进行从大到小的排序,然后修建kruskal重构树,这样就弄出了一颗以海拔为关键字的小根堆。然后对于每一棵子树,如果询问中的水位线是低于子树的根节点的,那么此时这棵子树中的所有叶子结点都是连通的。放到题中就是说这颗子树中任选一个点出发,到子树中的其它点都不需要花费。则它到1的实际开支为这些点中到1的最短路的最小值,这个最小值是在不考虑海平线的前提下,尽量走最短路径的权值。
然后我们假设对于当前询问,我们找到了一个子树的根节点u,满足d[u]>p且d[fa[u]]<=p (d[i]代表i点海拔)且出发点v在子树中,这时从v出发可以直接抵达子树中的任意一个叶子结点。因此我们需要从众多叶子节点(即原图给的点)中选出一个距离1号点花费最小的。时间复杂度O(T*N*LogN)
算法流程如下:
我们首先要求出每个点到1号点的最小花费,这个直接dijstra+最短路预处理。然后是要建出kruskal重构树,再然后维护以每个点作为根节点时子树中距离1号点的最小花费,这个建完树后一个简单的dfs搞定。最后是如何找到点u,这时我们要让一个重要的算法登场:倍增算法。直接加上点权>p的限制在树上倍增即可。
#include<bits/stdc++.h>
#define N 400005
#define M 800005
using namespace std;
inline int read(){
int ans=0;
char ch=getchar();
while(!isdigit(ch))ch=getchar();
while(isdigit(ch))ans=(ans<<3)+(ans<<1)+(ch^48),ch=getchar();
return ans;
}
inline void write(int x)
{
if(x>9)write(x/10);
putchar(x%10+'0');
}
int n,m,T,q,k,s,vis[N],first[N<<1],head[N],cntx=0,d[N],dep[N],f[N][20],fa[N<<1],lastans=0,totx=0;
struct Node、
{
int u,v,l,a;
}e[M],p[N<<1];
struct edge
{
int v,next;
}tr[M<<1];
struct node
{
int v,next,w;
}t[M];
struct heap
{
int u,v;
};
inline bool operator<(heap a,heap b){return a.v>b.v;}
inline void dijstra(int s=1) //找出每个点到s的最短路
{
memset(vis,false,sizeof(vis));
memset(d,0x3f,sizeof(d));
priority_queue<heap>q;
d[s]=0;
q.push((heap){s,d[s]});
while(!q.empty()){
heap x=q.top();
q.pop();
if(vis[x.u])continue;
vis[x.u]=true;
for(int i=head[x.u];i;i=t[i].next){
int v=t[i].v;
if(vis[v])continue;
if(d[v]>d[x.u]+t[i].w){
d[v]=d[x.u]+t[i].w
;
q.push((heap){v,d[v]});
}
}
}
for(int i=1;i<=n;++i)
p[i].l=d[i];//结果放到p[i].l中
}
inline bool cmp(Node a,Node b)
{
return a.a>b.a;
}
inline int find(int x)
{
return x==fa[x]?fa[x]:fa[x]=find(fa[x]);
}
inline void add(int u,int v)//重构树是用来连边的
{
tr[++cntx].v=v;
tr[cntx].next=first[u];
first[u]=cntx;
}
inline void addx(int u,int v,int w)//原图连边用的,带权
{
t[++totx].v=v;
t[totx].next=head[u];
t[totx].w=w;
head[u]=totx;
}
inline void dfs(int u,int pa)
{
dep[u]=dep[pa]+1,f[u][0]=pa;
for(int i=1;i<=19;++i)f[u][i]=f[f[u][i-1]][i-1];
for(int i=first[u];i;i=tr[i].next)
{
int v=tr[i].v;
dfs(v,u);
p[u].l=min(p[u].l,p[v].l);
//u,v是相连的,也就是说如果这边的海拔线高于规定的话,则从u,v之间可以直达
//于是要选两者的最小值
//u要么与两个叶子点相连,要么与一个叶子点一个新增点相连
//最终u为以u为根的子树中,所有点到1的最短路
//也就是说如果能走到u点,则此时p[u].l就是其子树中某个点到1的最短路
}
}
inline int query(int x,int y)
{
for(int i=19;i>=0;--i)
if(dep[x]-(1<<i)>0&&p[f[x][i]].a>y)
//一直向上跳,只要所跳的点海拔高于规定值. 注意是高于,不是高于等于
x=f[x][i];
return p[x].l;
}
inline void kruskal()
{
int tot=0,cnt=n;
for(int i=1;i<=(n<<1);++i)
fa[i]=i;
sort(e+1,e+m+1,cmp);
for(int i=1;i<=m;++i)
{
int u=e[i].u,v=e[i].v;
int fx=find(u),fy=find(v);
if(fx!=fy){
add(++cnt,fx);
add(cnt,fy);
fa[fx]=cnt;
fa[fy]=cnt;
p[cnt].a=e[i].a;
++tot;
}
if(tot==n-1)break;
}
dfs(cnt,0);
while(q--)
{
int x=(k*lastans+read()-1)%n+1,y=(k*lastans+read())%(s+1);
write(lastans=query(x,y));
puts("");
}
}
int main(){
T=read();
while(T--){
lastans=0,n=read(),m=read();
memset(e,0,sizeof(e)),cntx=0,totx=0;
memset(first,0,sizeof(first));
memset(head,0,sizeof(head));
memset(f,0,sizeof(f));
for(int i=1;i<=m;++i)
e[i].u=read(),e[i].v=read(),e[i].l=read(),
e[i].a=read(),addx(e[i].u,e[i].v,e[i].l),addx(e[i].v,e[i].u,e[i].l);
for(int i=n+1;i<=(n<<1);++i) //注意是2*n个点,因为要新增n-1个点
p[i].l=0x3f3f3f3f;
dijstra();
q=read(),k=read(),s=read();
kruskal();
}
return 0;
}