可持久化并查集 by zky
n个集合 m个操作
操作:
1 a b 合并a,b所在集合
2 k 回到第k次操作之后的状态(查询算作操作)
3 a b 询问a,b是否属于同一集合,是则输出1否则输出0
0<n,m<=2*10^4
Input
Output
Sample Input
5 6
1 1 2
3 1 2
2 0
3 1 2
2 1
3 1 2
Sample Output
1
0
1
https://blog.csdn.net/Diogenes_/article/details/80820895
Sol:
采用可持久化线段树,动态开点。当要修改某个叶子点的值时就再开一个线段树出来。
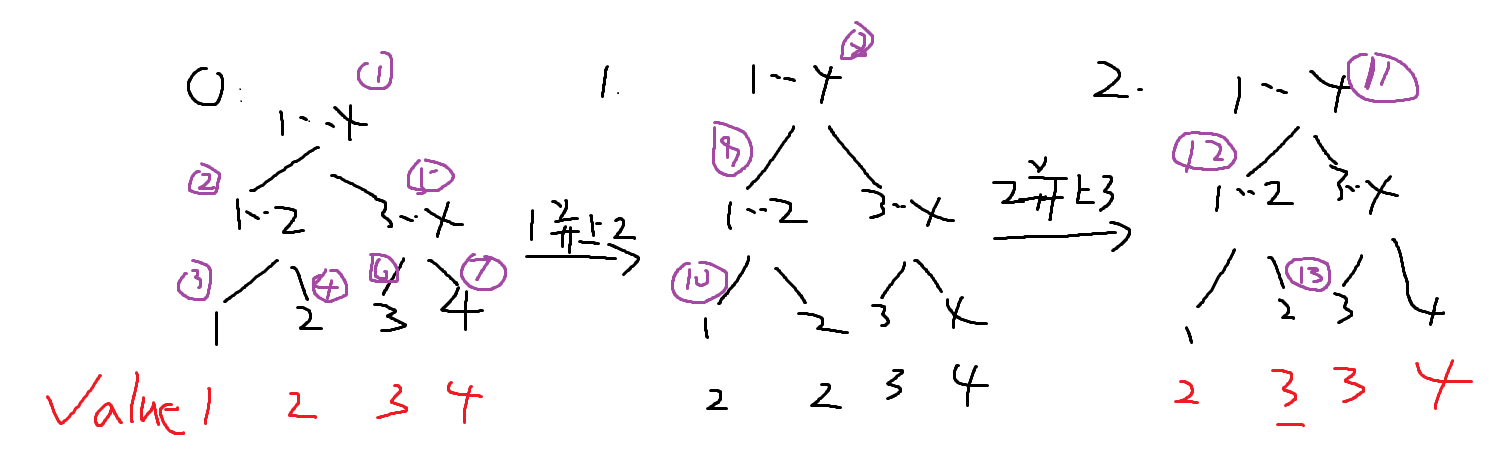
此时如果来询问1与3的关系时
先要找到1的父亲点是谁
于是在第2个线段树中找到1这个叶子点的权值为2
并不等于1。
于是在第2个线段树中继续找2这个叶子点的值为3
2不等于3
然后再在第2个线段树中找3这个叶子点的值为3
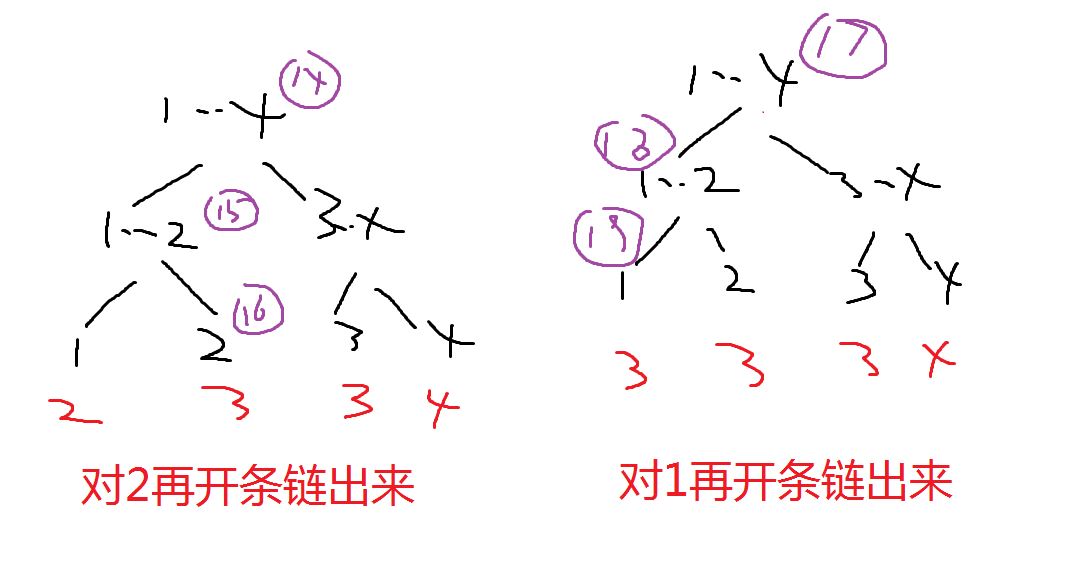
3等于3了,于是返回到上一层,新开一条链出来,
将2这个叶子点的值改为3.
再返回到上一层,新开一条链出来
将1这个叶子点的值也改为3
#include<bits/stdc++.h>
using namespace std;
#define F(i,j,n) for(int i=j;i<=n;i++)
#define D(i,j,n) for(int i=j;i>=n;i--)
#define ll long long
#define maxn 20005
#define maxm 3000000
using namespace std;
int n,m,p,x,y,cnt;
int rt[maxn],v[maxm],ls[maxm],rs[maxm];
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
void build(int &k,int l,int r)
{
k=++cnt;
if (l==r)
{
v[k]=l;
return;
}
int mid=(l+r)>>1;
build(ls[k],l,mid);
build(rs[k],mid+1,r);
}
int query(int k,int l,int r,int pos)
{
if (l==r)
return v[k];
int mid=(l+r)>>1;
if (pos<=mid)
return query(ls[k],l,mid,pos);
else
return query(rs[k],mid+1,r,pos);
}
void insert(int x,int &y,int l,int r,int pos,int val)
//要实现v[pos]的值改为val
//x是上一个版本的线段树
//y为当前版本的
//pos为位置,val为要设置的值
{
cout<<x<<" "<<y<<" "<<l<<" "<<r<<" "<<pos<<" "<<val<<endl;
char ww;
cin>>ww;
y=++cnt;
cout<<"cnt is "<<cnt<<endl;
if (l==r)
{
v[y]=val;
return;
}
int mid=(l+r)>>1;
ls[y]=ls[x];rs[y]=rs[x];
if (pos<=mid)
insert(ls[x],ls[y],l,mid,pos,val);
else
insert(rs[x],rs[y],mid+1,r,pos,val);
}
int find(int &root,int x)
{
int tmp=query(root,1,n,x);
//在第root个线段上找,区间为[x,x],也就是叶子点了
//其值为多少
if (tmp==x)
return x;
else
{
int ret=find(root,tmp);
//在当前的线段树上进行查找
insert(root,root,1,n,x,ret);
//并进行修改,x是位置,ret为所要变成的值
return ret;
}
}
int main()
{
n=read();m=read();
build(rt[0],1,n);
F(i,1,m)
{
p=read();
if (p==1) //1 a b 合并a,b所在集合
{
int x=read(),y=read(),
fx=find(rt[i-1],x),fy=find(rt[i-1],y);
if (fx==fy)
rt[i]=rt[i-1];
else
insert(rt[i-1],rt[i],1,n,fx,fy);
}
else if (p==2)
//2 k 回到第k次操作之后的状态(查询算作操作)
{
int x=read();
rt[i]=rt[x];
}
else
//3 a b 询问a,b是否属于同一集合,是则输出1否则输出0
{
int x=read(),y=read(),fx=find(rt[i-1],x),fy=find(rt[i-1],y);
if (fx==fy) puts("1");
else puts("0");
rt[i]=rt[i-1];
}
}
return 0;
}
//https://blog.csdn.net/AaronGZK/article/details/51511601
bzoj3674 加强版
自从zkysb出了可持久化并查集后……
hzwer:乱写能AC,暴力踩标程
KuribohG:我不路径压缩就过了!
ndsf:暴力就可以轻松虐!
zky:……
n个集合 m个操作
操作:
1 a b 合并a,b所在集合
2 k 回到第k次操作之后的状态(查询算作操作)
3 a b 询问a,b是否属于同一集合,是则输出1否则输出0
请注意本题采用强制在线,所给的a,b,k均经过加密,加密方法为x = x xor lastans,lastans的初始值为0
0<n,m<=2*10^5
Sample Input
5 6
1 1 2
3 1 2
2 1
3 0 3
2 1
3 1 2
Sample Output
1
0
1
就是加了强制在线
#include<cstdio>
#include<iostream>
using namespace std;
inline int read()
{
int x=0;char ch=getchar();
while(ch>'9'||ch<'0')ch=getchar();
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x;
}
int n,m,sz,last;
int root[200005],ls[10000005],rs[10000005],v[10000005],deep[10000005];
void build(int &k,int l,int r)
{
if(!k)k=++sz;
if(l==r){v[k]=l;return;}
int mid=(l+r)>>1;
build(ls[k],l,mid);
build(rs[k],mid+1,r);
}
void modify(int l,int r,int x,int &y,int pos,int val)
{
y=++sz;
if(l==r){v[y]=val;deep[y]=deep[x];return;}
ls[y]=ls[x];rs[y]=rs[x];
int mid=(l+r)>>1;
if(pos<=mid)
modify(l,mid,ls[x],ls[y],pos,val);
else modify(mid+1,r,rs[x],rs[y],pos,val);
}
int query(int k,int l,int r,int pos)
{
if(l==r)
return k;
int mid=(l+r)>>1;
if(pos<=mid)
return query(ls[k],l,mid,pos);
else
return query(rs[k],mid+1,r,pos);
}
void add(int k,int l,int r,int pos)
{
if(l==r){deep[k]++;return;}
int mid=(l+r)>>1;
if(pos<=mid)add(ls[k],l,mid,pos);
else add(rs[k],mid+1,r,pos);
}
int find(int k,int x)
{
int p=query(k,1,n,x);
if(x==v[p])
return p;
return find(k,v[p]);
}
int main()
{
n=read();m=read();
build(root[0],1,n);
int f,k,a,b;
for(int i=1;i<=m;i++)
{
f=read();
if(f==1)
{
root[i]=root[i-1];
a=read();b=read();
a=a^last;
b=b^last;
int p=find(root[i],a),q=find(root[i],b);
//这个程序是返回的位置
if(v[p]==v[q])
continue;
if(deep[p]>deep[q])
swap(p,q);
modify(1,n,root[i-1],root[i],v[p],v[q]);
if(deep[p]==deep[q])
add(root[i],1,n,v[q]);
}
if(f==2)
{k=read();k=k^last;root[i]=root[k];}
if(f==3)
{
root[i]=root[i-1];
a=read();
b=read();
a=a^last;
b=b^last;
int p=find(root[i],a),q=find(root[i],b);
if(v[p]==v[q])
last=1;
else
last=0;
printf("%d
",last);
}
}
return 0;
}