BP神经网络是深度学习的重要基础,它是深度学习的重要前行算法之一,因此理解BP神经网络原理以及实现技巧非常有必要。接下来,我们对原理和实现展开讨论。
1.原理
有空再慢慢补上,请先参考老外一篇不错的文章:A Step by Step Backpropagation Example
激活函数参考:深度学习常用激活函数之— Sigmoid & ReLU & Softmax
浅显易懂的初始化:CS231n课程笔记翻译:神经网络笔记 2
有效的Trick:神经网络训练中的Tricks之高效BP(反向传播算法)
通过简单演示BPNN的计算过程:一文弄懂神经网络中的反向传播法——BackPropagation
2.实现----Batch随机梯度法
这里实现了层数可定义的BP神经网络,可通过参数net_struct进行定义网络结果,如定义只有输出层,没有隐藏层的网络结构,激活函数为”sigmoid",学习率,可如下定义
net_struct = [[10,"sigmoid",0.01]] # 网络结构
如定义一层隐藏层为100个神经元,再接一层隐藏层为50个神经元,输出层为10个神经元的网络结构,如下
net_struct = [[100,"sigmoid",0.01],[50,"sigmoid",0.01],[10,"sigmoid",0.01]] # 网络结构
码农最爱的实现如下:

1 # # encoding=utf8 2 ''' 3 Created on 2017-7-3 4 5 @author: Administrator 6 ''' 7 import random 8 import pandas as pd 9 import numpy as np 10 from matplotlib import pyplot as plt 11 from sklearn.model_selection import train_test_split as ttsplit 12 13 class LossFun: 14 def __init__(self, lf_type="least_square"): 15 self.name = "loss function" 16 self.type = lf_type 17 18 def cal(self, t, z): 19 loss = 0 20 if self.type == "least_square": 21 loss = self.least_square(t, z) 22 return loss 23 24 def cal_deriv(self, t, z): 25 delta = 0 26 if self.type == "least_square": 27 delta = self.least_square_deriv(t, z) 28 return delta 29 30 def least_square(self, t, z): 31 zsize = z.shape 32 sample_num = zsize[1] 33 return np.sum(0.5 * (t - z) * (t - z) * t) / sample_num 34 35 def least_square_deriv(self, t, z): 36 return z - t 37 38 class ActivationFun: 39 ''' 40 激活函数 41 ''' 42 def __init__(self, atype="sigmoid"): 43 self.name = "activation function library" 44 self.type = atype; 45 46 def cal(self, a): 47 z = 0 48 if self.type == "sigmoid": 49 z = self.sigmoid(a) 50 elif self.type == "relu": 51 z = self.relu(a) 52 return z 53 54 def cal_deriv(self, a): 55 z = 0 56 if self.type == "sigmoid": 57 z = self.sigmoid_deriv(a) 58 elif self.type == "relu": 59 z = self.relu_deriv(a) 60 return z 61 62 def sigmoid(self, a): 63 return 1 / (1 + np.exp(-a)) 64 65 def sigmoid_deriv(self, a): 66 fa = self.sigmoid(a) 67 return fa * (1 - fa) 68 69 def relu(self, a): 70 idx = a <= 0 71 a[idx] = 0.1 * a[idx] 72 return a # np.maximum(a, 0.0) 73 74 def relu_deriv(self, a): 75 # print a 76 a[a > 0] = 1.0 77 a[a <= 0] = 0.1 78 # print a 79 return a 80 81 class Layer: 82 ''' 83 神经网络层 84 ''' 85 def __init__(self, num_neural, af_type="sigmoid", learn_rate=0.5): 86 self.af_type = af_type # active function type 87 self.learn_rate = learn_rate 88 self.num_neural = num_neural 89 self.dim = None 90 self.W = None 91 92 self.a = None 93 self.X = None 94 self.z = None 95 self.delta = None 96 self.theta = None 97 self.act_fun = ActivationFun(self.af_type) 98 99 def fp(self, X): 100 ''' 101 Foward Propagation 102 ''' 103 self.X = X 104 xsize = X.shape 105 self.dim = xsize[0] 106 self.num = xsize[1] 107 108 if self.W == None: 109 # self.W = np.random.random((self.dim, self.num_neural))-0.5 110 # self.W = np.random.uniform(-1,1,size=(self.dim,self.num_neural)) 111 if(self.af_type == "sigmoid"): 112 self.W = np.random.normal(0, 1, size=(self.dim, self.num_neural)) / np.sqrt(self.num) 113 elif(self.af_type == "relu"): 114 self.W = np.random.normal(0, 1, size=(self.dim, self.num_neural)) * np.sqrt(2.0 / self.num) 115 if self.theta == None: 116 # self.theta = np.random.random((self.num_neural, 1))-0.5 117 # self.theta = np.random.uniform(-1,1,size=(self.num_neural,1)) 118 119 if(self.af_type == "sigmoid"): 120 self.theta = np.random.normal(0, 1, size=(self.num_neural, 1)) / np.sqrt(self.num) 121 elif(self.af_type == "relu"): 122 self.theta = np.random.normal(0, 1, size=(self.num_neural, 1)) * np.sqrt(2.0 / self.num) 123 # calculate the foreward a 124 self.a = (self.W.T).dot(self.X) 125 ###calculate the foreward z#### 126 self.z = self.act_fun.cal(self.a) 127 return self.z 128 129 def bp(self, delta): 130 ''' 131 Back Propagation 132 ''' 133 self.delta = delta * self.act_fun.cal_deriv(self.a) 134 self.theta = np.array([np.mean(self.theta - self.learn_rate * self.delta, 1)]).T # 求所有样本的theta均值 135 dW = self.X.dot(self.delta.T) / self.num 136 self.W = self.W - self.learn_rate * dW 137 delta_out = self.W.dot(self.delta); 138 return delta_out 139 140 class BpNet: 141 ''' 142 BP神经网络 143 ''' 144 def __init__(self, net_struct, stop_crit, max_iter, batch_size=10): 145 self.name = "net work" 146 self.net_struct = net_struct 147 if len(self.net_struct) == 0: 148 print "no layer is specified!" 149 return 150 151 self.stop_crit = stop_crit 152 self.max_iter = max_iter 153 self.batch_size = batch_size 154 self.layers = [] 155 self.num_layers = 0; 156 # 创建网络 157 self.create_net(net_struct) 158 self.loss_fun = LossFun("least_square"); 159 160 def create_net(self, net_struct): 161 ''' 162 创建网络 163 ''' 164 self.num_layers = len(net_struct) 165 for i in range(self.num_layers): 166 self.layers.append(Layer(net_struct[i][0], net_struct[i][1], net_struct[i][2])) 167 168 def train(self, X, t, Xtest=None, ttest=None): 169 ''' 170 训练网络 171 ''' 172 eva_acc_list = [] 173 eva_loss_list = [] 174 175 xshape = X.shape; 176 num = xshape[0] 177 dim = xshape[1] 178 179 for k in range(self.max_iter): 180 # i = random.randint(0,num-1) 181 idxs = random.sample(range(num), self.batch_size) 182 xi = np.array([X[idxs, :]]).T[:, :, 0] 183 ti = np.array([t[idxs, :]]).T[:, :, 0] 184 # 前向计算 185 zi = self.fp(xi) 186 187 # 偏差计算 188 delta_i = self.loss_fun.cal_deriv(ti, zi) 189 190 # 反馈计算 191 self.bp(delta_i) 192 193 # 评估精度 194 if Xtest != None: 195 if k % 100 == 0: 196 [eva_acc, eva_loss] = self.test(Xtest, ttest) 197 eva_acc_list.append(eva_acc) 198 eva_loss_list.append(eva_loss) 199 print "%4d,%4f,%4f" % (k, eva_acc, eva_loss) 200 else: 201 print "%4d" % (k) 202 return [eva_acc_list, eva_loss_list] 203 204 def test(self, X, t): 205 ''' 206 测试模型精度 207 ''' 208 xshape = X.shape; 209 num = xshape[0] 210 z = self.fp_eval(X.T) 211 t = t.T 212 est_pos = np.argmax(z, 0) 213 real_pos = np.argmax(t, 0) 214 corrct_count = np.sum(est_pos == real_pos) 215 acc = 1.0 * corrct_count / num 216 loss = self.loss_fun.cal(t, z) 217 # print "%4f,loss:%4f"%(loss) 218 return [acc, loss] 219 220 def fp(self, X): 221 ''' 222 前向计算 223 ''' 224 z = X 225 for i in range(self.num_layers): 226 z = self.layers[i].fp(z) 227 return z 228 229 def bp(self, delta): 230 ''' 231 反馈计算 232 ''' 233 z = delta 234 for i in range(self.num_layers - 1, -1, -1): 235 z = self.layers[i].bp(z) 236 return z 237 238 def fp_eval(self, X): 239 ''' 240 前向计算 241 ''' 242 layers = self.layers 243 z = X 244 for i in range(self.num_layers): 245 z = layers[i].fp(z) 246 return z 247 248 def z_score_normalization(x): 249 mu = np.mean(x) 250 sigma = np.std(x) 251 x = (x - mu) / sigma; 252 return x; 253 254 def sigmoid(X, useStatus): 255 if useStatus: 256 return 1.0 / (1 + np.exp(-float(X))); 257 else: 258 return float(X); 259 260 def plot_curve(data, title, lege, xlabel, ylabel): 261 num = len(data) 262 idx = range(num) 263 plt.plot(idx, data, color="r", linewidth=1) 264 265 plt.xlabel(xlabel, fontsize="xx-large") 266 plt.ylabel(ylabel, fontsize="xx-large") 267 plt.title(title, fontsize="xx-large") 268 plt.legend([lege], fontsize="xx-large", loc='upper left'); 269 plt.show() 270 271 if __name__ == "__main__": 272 print ('This is main of module "bp_nn.py"') 273 274 print("Import data") 275 raw_data = pd.read_csv('./train.csv', header=0) 276 data = raw_data.values 277 imgs = data[0::, 1::] 278 labels = data[::, 0] 279 train_features, test_features, train_labels, test_labels = ttsplit( 280 imgs, labels, test_size=0.33, random_state=23323) 281 282 train_features = z_score_normalization(train_features) 283 test_features = z_score_normalization(test_features) 284 sample_num = train_labels.shape[0] 285 tr_labels = np.zeros([sample_num, 10]) 286 for i in range(sample_num): 287 tr_labels[i][train_labels[i]] = 1 288 289 sample_num = test_labels.shape[0] 290 te_labels = np.zeros([sample_num, 10]) 291 for i in range(sample_num): 292 te_labels[i][test_labels[i]] = 1 293 294 print train_features.shape 295 print tr_labels.shape 296 print test_features.shape 297 print te_labels.shape 298 299 stop_crit = 100 # 停止 300 max_iter = 10000 # 最大迭代次数 301 batch_size = 100 # 每次训练的样本个数 302 net_struct = [[100, "relu", 0.01], [10, "sigmoid", 0.1]] # 网络结构[[batch_size,active function, learning rate]] 303 # net_struct = [[200,"sigmoid",0.5],[100,"sigmoid",0.5],[10,"sigmoid",0.5]] 网络结构[[batch_size,active function, learning rate]] 304 305 bpNNCls = BpNet(net_struct, stop_crit, max_iter, batch_size); 306 # train model 307 308 [acc, loss] = bpNNCls.train(train_features, tr_labels, test_features, te_labels) 309 # [acc, loss] = bpNNCls.train(train_features, tr_labels) 310 print("training model finished") 311 # create test data 312 plot_curve(acc, "Bp Network Accuracy", "accuracy", "iter", "Accuracy") 313 plot_curve(loss, "Bp Network Loss", "loss", "iter", "Loss") 314 315 316 # test model 317 [acc, loss] = bpNNCls.test(test_features, te_labels); 318 print "test accuracy:%f" % (acc) 319
实验数据为mnist数据集合,可从以下地址下载:https://github.com/WenDesi/lihang_book_algorithm/blob/master/data/train.csv
a.使用sigmoid激活函数和net_struct = [10,"sigmoid"]的网络结构(可看作是softmax 回归),其校验精度和损失函数的变化,如下图所示:
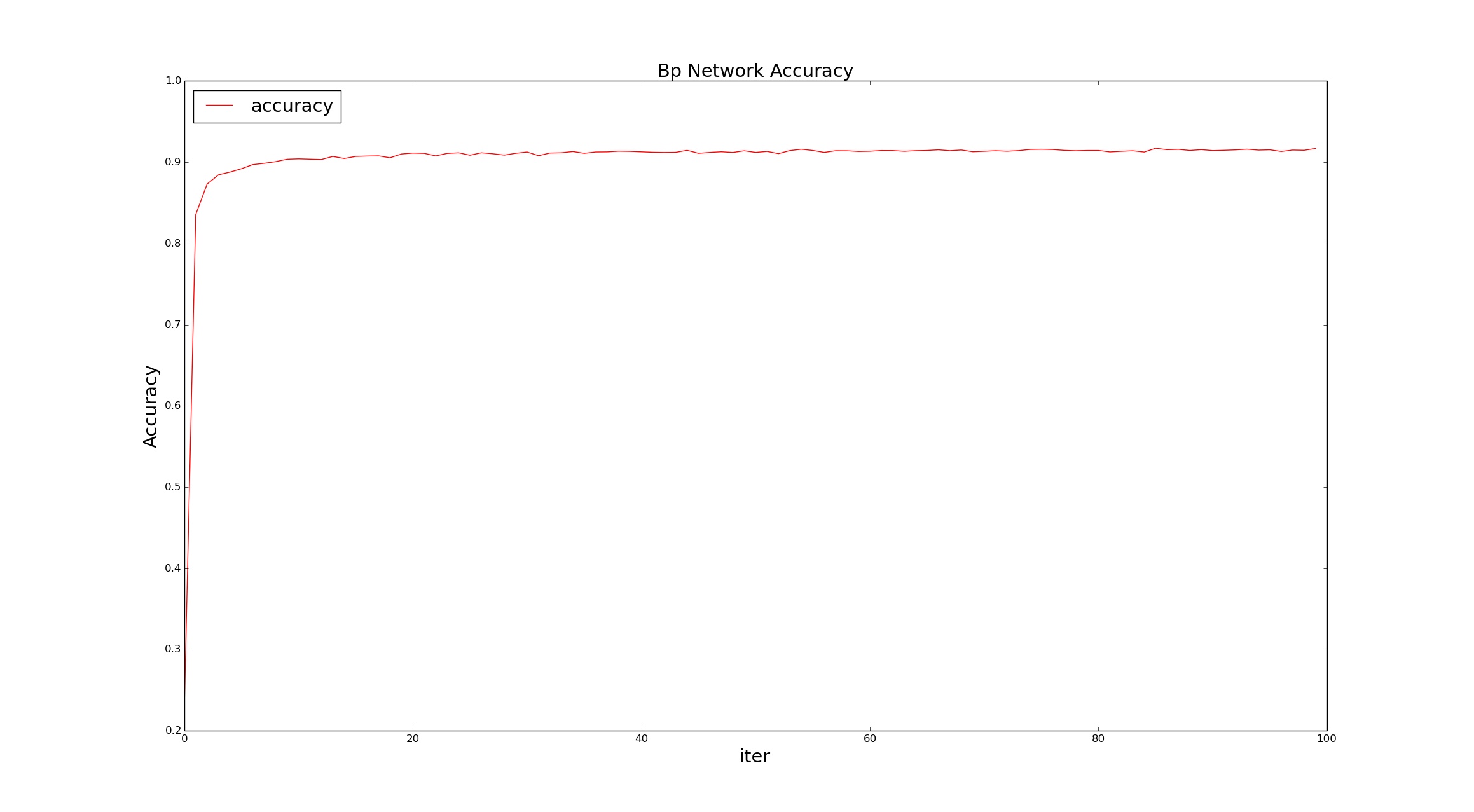

测试精度达到0.916017,效果还是不错的。但是随机梯度法,依赖于参数的初始化,如果初始化不好,会收敛缓慢,甚至有不理想的结果。
b.使用sigmoid激活函数和net_struct = [200,"sigmoid",100,"sigmoid",10,"sigmoid"] 的网络结构(一个200的隐藏层,一个100的隐藏层,和一个10的输出层),其校验精度和损失函数的变化,如下图所示:
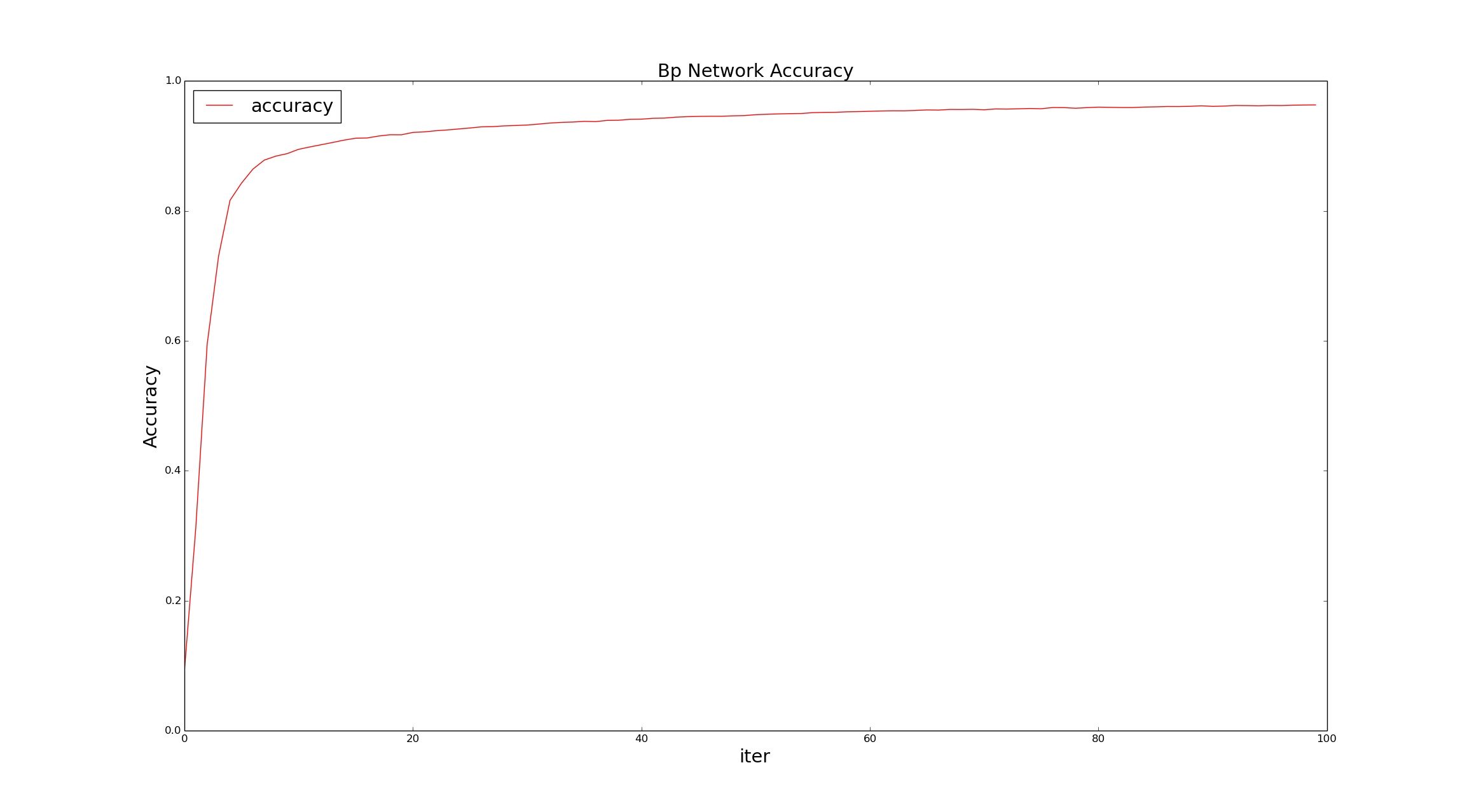

其校验精度达到0.963636,比softmax要好不少。从损失曲线可以看出,加入隐藏层后,算法收敛要比无隐藏层的稳定。
