循环神经网络——反对称RNN模型
本文主要介绍的是循环神经网络RNN及其研究进展，其中的主要内容来自于一篇2019年的ICLR论文，论文原文如下
AntisymmetricRNN: A Dynamical System View on Recurrent Neural Networks一、RNN与LSTM
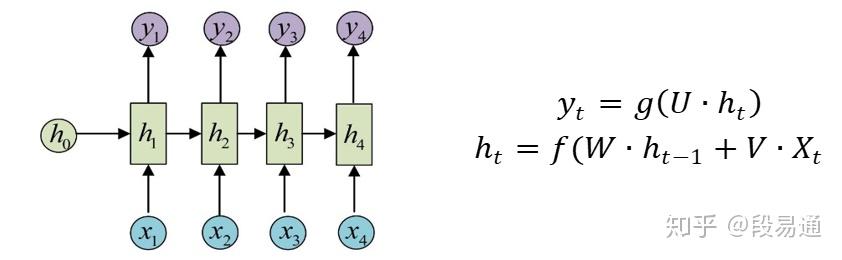
在机器学习领域中，循环神经网络（RNN）可以说是一块相当重要的组成部分了，由于它能够在处理新数据的时候将之前的数据也考虑进来，所以RNN在序列数据的建模中有着广泛的应用，例如机器翻译任务，我们在翻译一个单词时，如果能将之前已经翻译输入的单词信息也考虑进去的话，那么翻译的肯定会更加准确。为了达到这样目的，RNN采用了如下图所示的结构，其计算过程如下式所示，其中U、W和V都是权重参数。
循环神经网络
可以看出，对于RNN，在计算隐层值 时，输入的不仅有样本数据
，还有RNN在之前的计算出来的隐层值
，从而将之前的信息也考虑了进来，这就是RNN的原理。
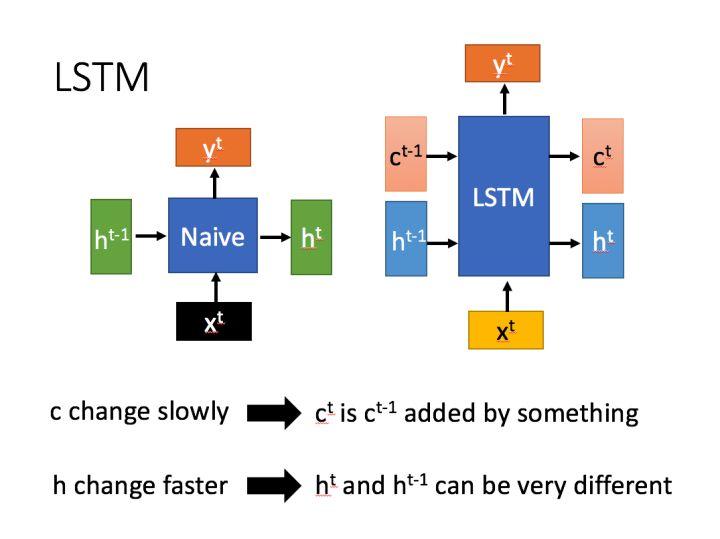
但是RNN也存在着一些问题，虽然它能够用于对序列数据建模，但是当序列较长的时候，它就会出现梯度消失和梯度爆炸的问题，而这样就使得它在实际应用中收到了很大的限制。为了解决这个问题，LSTM应运而生，它是RNN的一个变种，下面是原始RNN和LSTM的结构对比。
RNN与LSTM
可以看出，LSTM比原始的RNN多了一个传递状态 。在LSTM中，传递状态
一般改变得很慢，通常是上一个状态
加上一些数值；
则往往变化很大，这也是模型叫做LSTM（Long short-term memory）的原因。
下面是LSTM的内部结构，首先类似于原始RNN，将输入的 和之前的状态
拼接起来一起作为输入，不过LSTM不是直接计算
，而是先计算得到四个状态：
，其中的
是用来作为门控状态，左图中的
代表sigmoid激活函数。右图是计算过程，其中
代表Hadamard Product，就是将矩阵中的每一个对应元素相乘，而+就是矩阵加法。
LSTM内部结构
具体来说，LSTM主要分为三个阶段，首先是忘记阶段，由忘记门控来控制对于 的忘记；接着是选择记忆阶段，通过输入门控
来实现对于输入内容z的选择记忆；最后是输出阶段，由输出门控
来控制输出的
，然后再由
得到结果
。
利用门控状态来实现对于隐状态传输的控制，这就是LSTM的基本思想，显然这样的方式比之前的RNN更加灵活，不过也由于这些门控状态的引入，导致了需要学习的参数更多，训练难度更大，而接下来介绍的这种反对称RNN方法，则从另一个角度对进行了思考与改进。
二、反对称RNN
1.常微分方程与前向欧拉法
接下来进入正文，先明确一下RNN需要改进的地方，那就是它对于长序列的建模能力较差。对于这个问题，LSTM采用的是门控信号来对模型进行改进，而接下来将从求常微分方程（ODE）的数值解的角度来分析这个问题。
考虑如下的一阶ODE
给定初始状态h(0)，现在想要求函数h随时间t的变化，也就是求h(t)。这样的问题在很多情况下是没有解析解的，需要利用数值逼近的方法，前向欧拉法就是一个代表，它的原理很简单，公式如下：
其中 被叫做步长，一般是一个很小的数字。
现在考虑下面的ODE
用前向欧拉法求解，则有
2.ODE的稳定性
可以发现，如果将看作隐层状态，这样的形式与RNN是很相似的（先不考虑输入数据X），因此可以把对于RNN的要求放在ODE中来研究。首先对于RNN，我们希望它是对神经网络隐层状态的初值不敏感的，或者说是稳定的，否则结果将会因为初值的些许变化而完全不同；另外，我们也不希望RNN太“稳定”，如果对于不同的输入，最终的结果全部都趋于一致，那么RNN也就失去了信息获取的能力，也就是RNN完全“遗忘”了之前输入的信息，这被叫做耗散系统。所以需要构造这样一个“恰到好处”的RNN——既能够记忆到之前输入的历史信息，同时也不会让历史信息对其造成过大的影响。
幸运的是，ODE的数值求解方法已经对这些问题有了很深入的研究，先来看ODE关于稳定性的定义：
有如下命题：
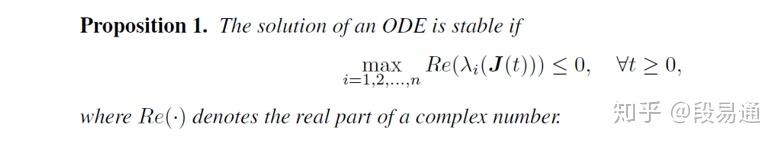
其中 是函数f的雅可比矩阵（
），而
代表矩阵的第i个特征值。
为了实现上面的要求，只满足稳定性还不够，还要防止它成为一个耗散系统，经过研究发现， 时会导致耗散系统的出现，因此需要做的就是令
，这样的临界状态就能够满足要求——稳定且能长期记忆（证明见附录1）。
那么现在的目标就是去找到一个满足临界状态的ODE，从论文题目就可以看出来，这里用到的是反对称矩阵（即 ），用反对称矩阵的原因是它的特征值都是虚数，也就是说
，满足之前的要求。这样就可以构造出满足条件的ODE了，其形式如下：
其中x(t)是输入的数据， 是偏置，对于这样的式子，其雅可比矩阵为：
由于 是一个反对称矩阵，因此
的特征值都是虚数（证明见附录2），即有对于任意i，
。这样就有了合适的ODE，则由前向欧拉法可得：
另外，由于 是反对称的，因此对于
只需要令其为一个上三角矩阵即可，这样学习的参数减少为
，效率更高。
3.前向欧拉法的稳定性
前面讨论的是如何构造一个稳定的ODE式子，但是仅仅这些还不够，因为之前讨论前提都是关于解析解的，而RNN其实用的是前向欧拉法来得到数值逼近解，因此想有稳定解，不止要考虑ODE，还要考虑前向欧拉法的稳定解条件，其条件如下：
可以发现，之前构造的反对称式子并不能满足这个条件，所以需要做一些修正：
其中 是单位矩阵，
。添加的这一项叫做扩散项，这样一来，雅可比矩阵将会有一个小的负实部，这样就可以在满足上面条件的同时，也可以满足
的条件。
4.门控机制
LSTM表明，门控机制对于RNN是至关重要的，因此也可以将门控机制加入到反对称RNN中，不过需要注意保证仍满足临界条件，如下所示：
其中 是sigmoid函数，
是Hadamard product。
加入门控状态后的雅可比矩阵仍然是一个对角矩阵乘以一个反对称矩阵的形式（忽略扩散项），因此仍满足条件，而这就是反对称RNN的最终形式，另外可以看出，它还利用了类似于残差连接（skip connect）的方式，这样就能够更有效解决深度网络中出现的梯度爆炸和消失的问题。
5.仿真与实验
下面是一些不同种类RNN的隐层状态可视化图，其中五角星代表初始隐层状态h(0)，通过对比隐状态h的运动轨迹可以发现，反对称RNN中h(t)大小的变化确实很稳定，符合之前的预期。
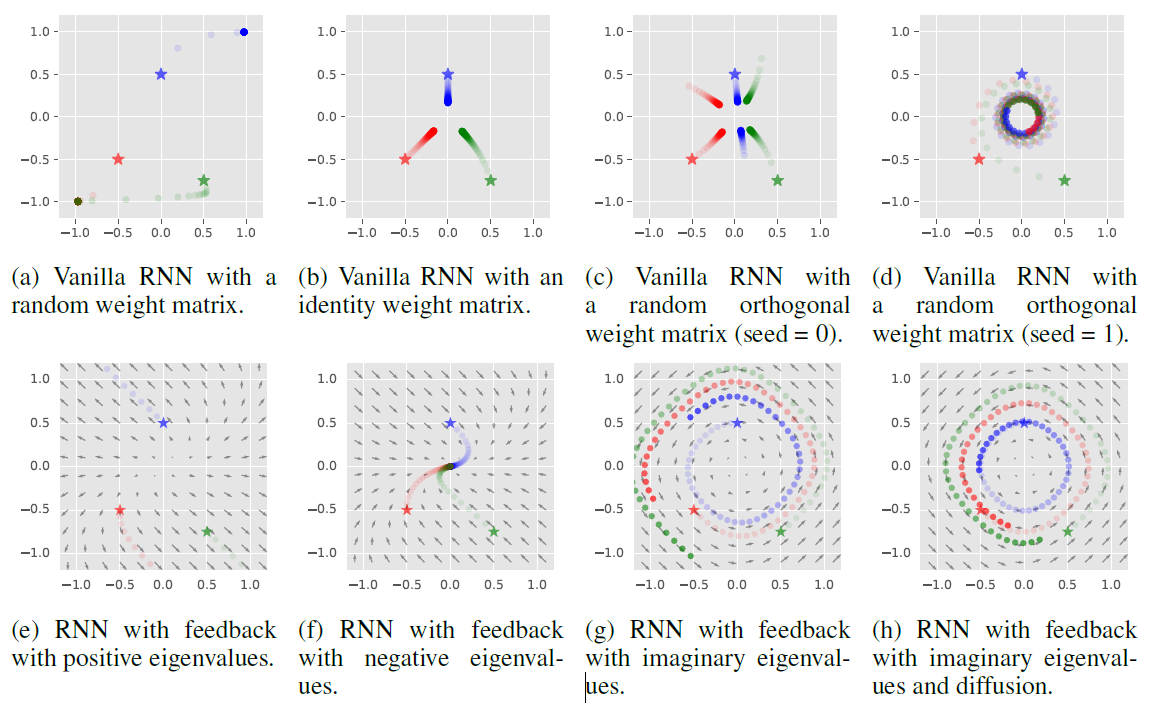RNN隐状态的运动轨迹
反对称RNN在实际实验中的表现也很好，下图是不同的RNN模型在CIFAR-10中的表现
这里主要说一下noise padded任务，它先输入的是需要分类的图像，而之后输入的则是标准高斯噪声，这样的话就很考察模型的记忆能力了，可以看出反对称RNN的表现比LSTM强不少。
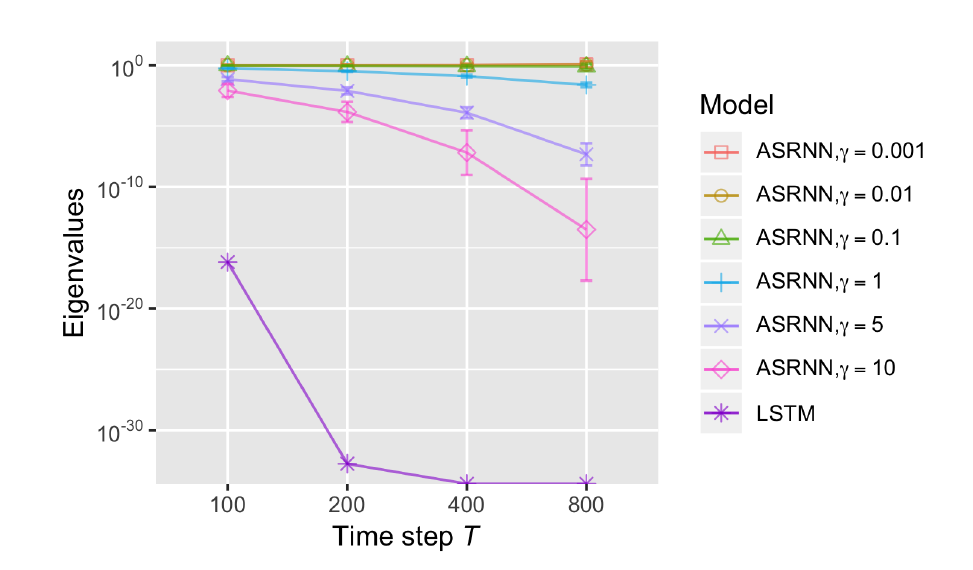
通过下图可以看出，随着时间步长t的增加，LSTM的雅可比矩阵的特征值迅速衰减为零，这表明在反向传播中出现了梯度消失，所以LSTM的效果并不好。而对于反对称RNN(ASRNN)，其特征值均值的可以保持在1附近，这意味着没有梯度消失和梯度爆炸，不过对于较大的也会出现梯度消失，而较小的则不能保证欧拉法的稳定性，因此的取值需要在长期记忆和稳定性之间权衡。
三、总结
这篇文章从常微分方程的角度出发，分析了RNN要想实现稳定的长期记忆需要满足什么条件，并通过构造反对称矩阵的方式改进了RNN，实现了性能上的改进。而这也启示我们可以从其它ODE的数值解法的角度来分析并改进RNN。
附录1
这里证明一下为什么 能够让ODE满足稳定且能长期记忆的要求，先来看一个标量ODE：
，可以得到解
，而对于不同的初始值
和
，则有
可以看出，若 ，则初值的一点改变就会导致指数级发散；而若
，则虽然稳定了，但是初值的改变对结果的影响太小，这也不是我们想要的，因此只能尽量让
。
现在来看一个矩阵ODE： ，其中
和
是向量，
是一个矩阵，其解是
。
为了简单起见，认为是 一个可对角化矩阵，即有
，其中
是
的特征值对角矩阵，P是特征向量矩阵，那么就可以将ODE变为
令 ，则有
那么对于 中的每一个元素，都有一个标量ODE
那么套用上面的结论可知，只有对于任意 ，均有
时，才能使ODE满足要求。
现在来看RNN，我们希望对于隐状态 的变化不会导致
出现指数增长或减小，也就是希望
不要随t指数增长或减小，令
，则有
套用上面的结论，要想使得 满足要求，则需
，证明完成。
附录2
参考资料
[1] ANTISYMMETRICRNN: A DYNAMICAL SYSTEM VIEW ON RECURRENT NEURAL NETWORKS
[2] 人人都能看懂的LSTM
文章被以下专栏收录
推荐阅读
RNN循环神经网络—梯度爆炸和消失的简单解析
通过cs224n关于循环神经网络一章的内容，以及自己对其他相关论文和博客的研读后，发现对循环神经网络中BPTT（即backpropagation through time）中，关于产生梯度爆炸和梯度消失的数学推导不…
Step-by-step to LSTM: 解析LSTM神经网络设计原理
RNN(循环神经网络)-2
还没有评论