zoukankan      html  css  js  c++  java

  • 《【公开课】斯坦福李飞飞教授最新cs231n计算机视觉经典课程》

    【公开课】斯坦福李飞飞教授最新cs231n计算机视觉经典课程

     

    视频选集

    7/34

      

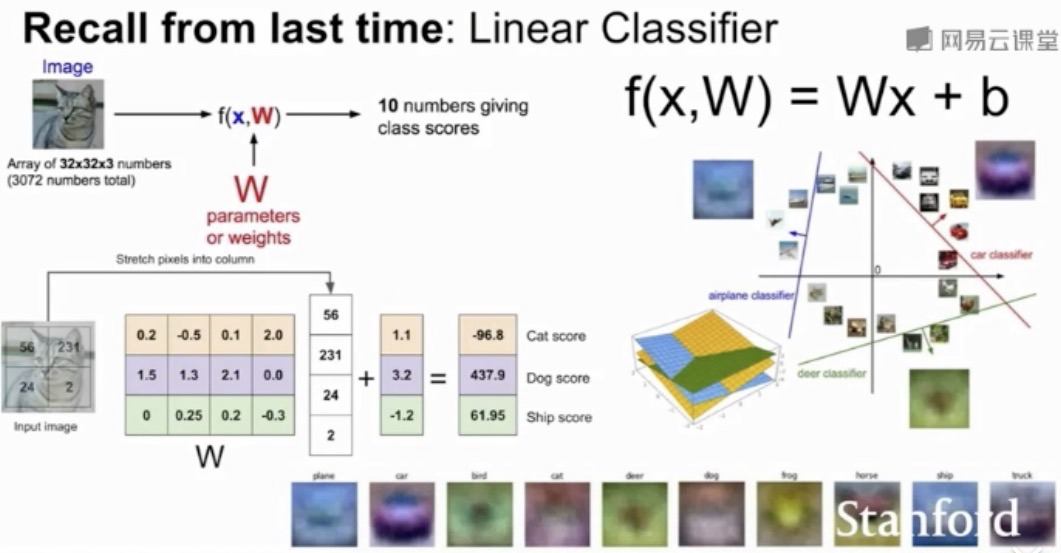
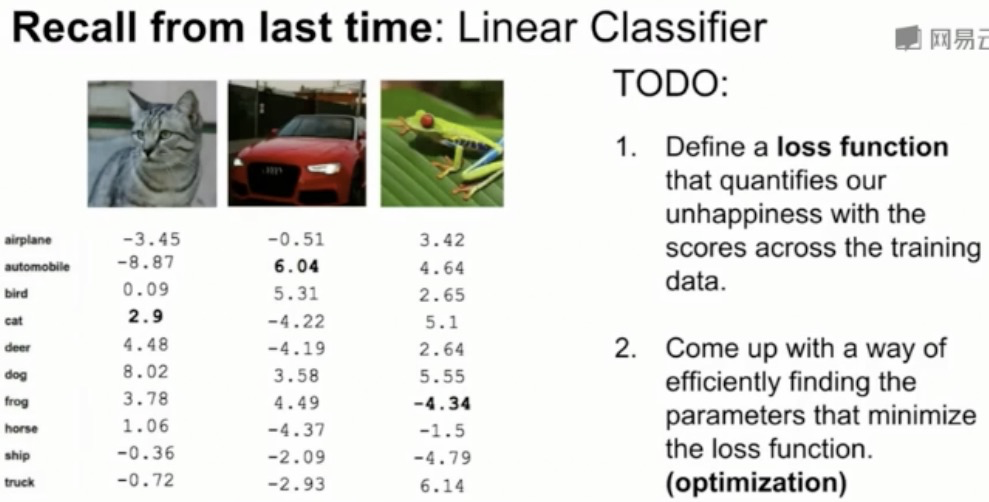
    初始Loss：C-1

    0>= s_j - s_yj +1 => s_j<= s_yj-1 ，有一个安全间隔，s_j（错误分类）只要比 s_yj 少1 就好了，一定要至少少1，再少太多就不关心了；

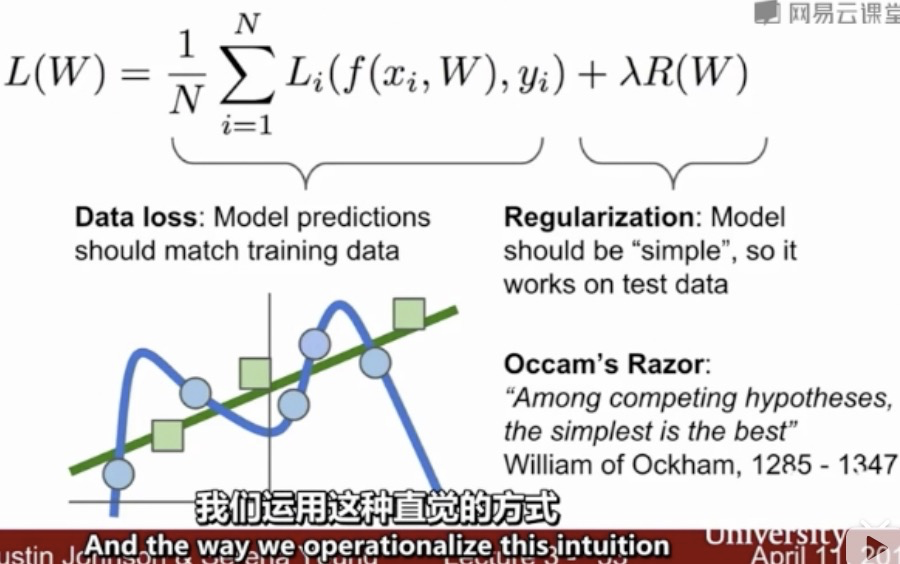
    --> 取参数 delta ，只要fitted curve 在 点的 delta-TR 邻域内；—— delta 可以根据点集密度 Bayesian 调整 ——

    • 在TR邻域内采样（均匀采样？采多少比例？）——如何评价邻域的覆盖度好坏？
    • 只要deviation 在delta 以内，就算 fit 住？ 

    点稀的地方应 min 波动 --> 兼顾 全局 & 局部 

    先高阶多项式，然后再根据样本点局部加权插值调整？

    先找样本点的“闭包”？

    partially-observable  LS？

    需要在多大的范围内 采样 和 fit ？——离所有样本点（+ TR 采样点）都要比较“近”，max deviation 需要contrained 住 

    样本少 + 模型容量大，才容易过拟合

    statistically fit v.s. 样本点 fit 

    样本点 fit v.s. 置信度/区间？

    如何刻画一条曲线的“波动/平滑程度”？

    样本点少，根本不足以判断是一次还是二次还是三次，能用一次 fit 就用一次 fit，因为二次的局部就是一次

    “simple” —— 二次、三次也可以很 simple ....，不一定次数高就比次数低复杂... —— 比如可以拿一个二次或三次的局部（近似线性）... 

    所以问题的关键是：在样本所在的前后一段区间范围内，曲线不能波动太大... 要“平稳” 

    平稳——cconvex hull 面积（体积）要小？

    平稳——当新增加样本点之后，模型不能变化太大？
    拟合曲线上新取点，离群度低—— loss 函数 边际增加小

    --> 以现有样本点“似然”，新样本点呈 Gaussian 状分布？

    ——点稀的地方，过拟合的曲线变异更大！！——点稀的地方，应该更“保守”——更从“局部”考虑；——loss 不应该用 1/N 平均加权，mixture Gaussian 密度更小的地方，更应该和附近的已知样本点保持平滑 ——越稀越平滑 —— mixture Gaussian 密度更小的地方，直接局部插值——增加（从已知样本点插值得到的新）样本点；反倒是 mixture Gaussian 密度更大的地方（已知样本点的地方），需要 loose fit tolerance ... 

    1/N loss function 加权系数，应该与样本点的密度成反比

    连续 n 次 v.s. 离散（分段线性），哪种方式更可取？分几段？数值问题了... 

    二次还是三次，和一般的 lambda * 0/1/2 范数，还不一样 ... 

    Fancier？

    stochastic depth？

     

     L2 正则对应 Gaussian prior 的MAP推断

     

    P6：

    P6【06】2.2 图像分类-线性分类1

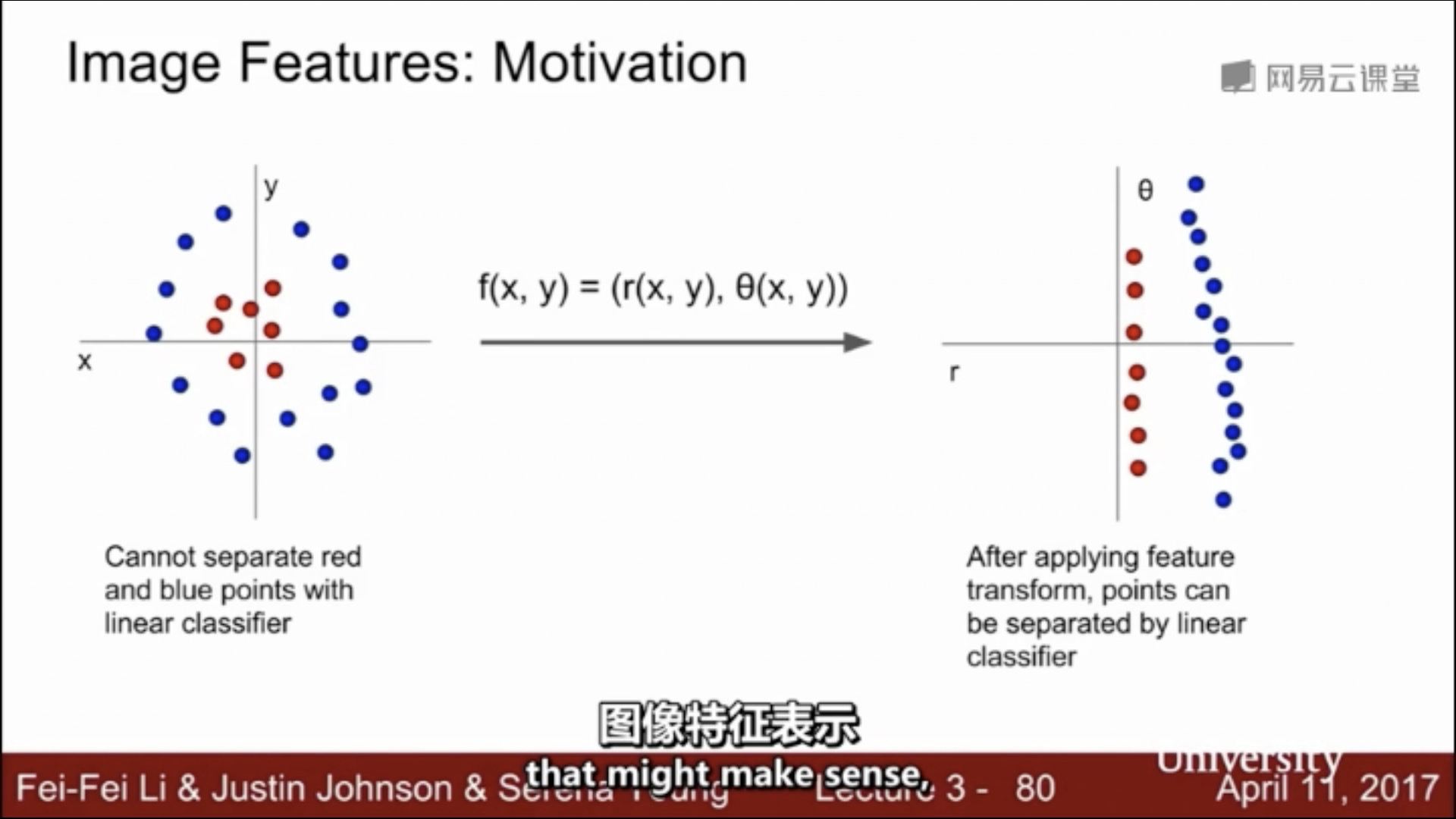
    核心：非线性特征变换 + 线性分类器？

    --> 非线性分类器？

     --> HoG 旁路 + CNN DL？

    two-stage -> end-to-end 

    模型（连续地）选 vocab 

    -->

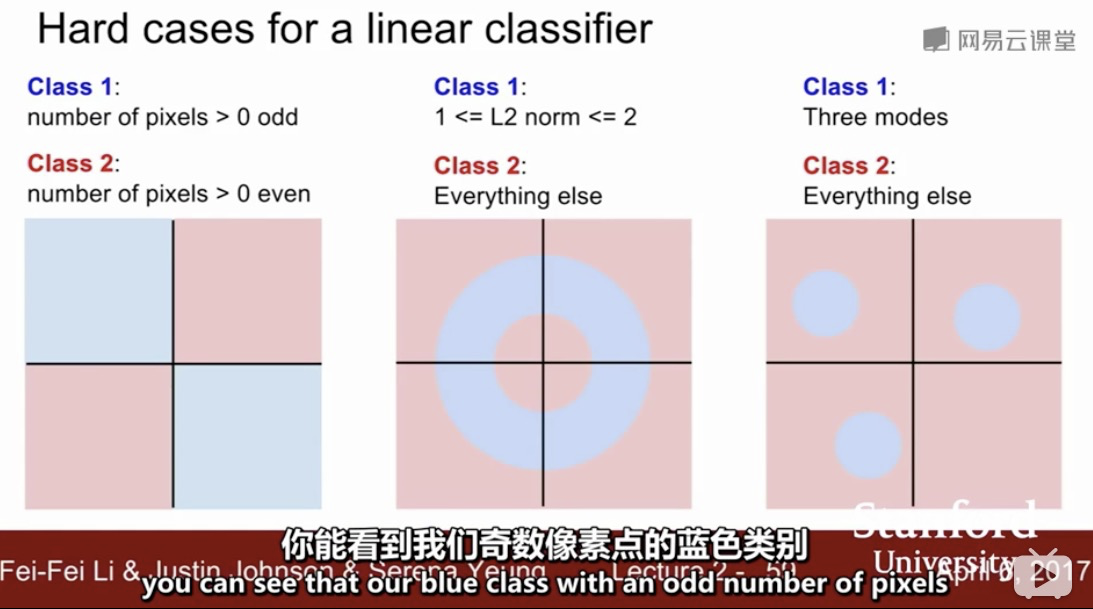
    线性不可分：一个超平面不可分，多个超平面也不可分 ... 上图中间case 是 无穷超平面不可分。。。进一步将 线性不可分 的概念精细化

    -->

    线性不可分：一定是一个 “低维流形”上的概念；因为只要升维（比如最严重的情形 data leakage：直接加入 label 维，则一定可分~）——这不是我们想要的，我们想要的是“Bayesian 常识”层面的升维；比如经典的平面上“新月形”两类不可分，但升至三维即可分的例子——实际上是 data leakage 了 ... 但这个 data leakage 可以通过某种 “平滑/常识”（高维曲线嵌入低维流形形成数据集--我们要做的是从这个低维数据集去推断最可能的高维曲线，满足一定的目标指标最小化--> 逆流形学习？？）这才是真正的“学习”，而不是简单的分类；

    但实际上正常一般的机器学习模型就是在干类似的事情？怎么来定义和衡量这个“目标指标”？--参考“流形学习”的内容

    • 高维（可分）：正类、负类、超平面 S —— 未知，需要推断
    • 低维（不可分）：正类、负类、超平面在低维的投影 P —— 未知（P亦未知），P和S有投影关系：在这个投影关系上下手做文章？
      • 　　P不唯一，在升维的这个维度上，截距不同则不同，需要“中心化”——升维不止一个维度

    CTR预估，CoEC 的原理其实有点类似；但只是 sparse (rating) click matrix 上的 look alike；—— 对应到一般的ML分类/回归问题上呢？怎么定义“常识”并incorporate 进来？

    特征工程只是在低维流形上对现有维度特征各种组合...是假“升维”，不太可能预测到真“升维”？... —— 真升维应该从 label 入手（比如现有特征多和 CoEC 这种特征做交叉组合...）... 可以发展一套系统化地升维的办法论...  

    embedding，模型角度是升维，先降维至dense 向量空间，再喂入分类模型 --> 这两个阶段 end to end 一起训练。。。其实是 encoder-decoder 架构 ... 那 wide 部分相当于是 U-net 或 dense-net 的直连？可以系统化地搞，连各种 high way，效果说不定好 ... 就是高层能直接见到底层的特征~AutoML了... 上界在哪？

    CoEC 也有一个很隐晦的 data leakage 的问题——样本是有时间点的，也应该滚动地给，应该会有提升~

    多分类，Hauffmann 树可能有帮助，一层一层选（这里的层可以是商品类目、可以召回的通路 ... 等等）

    BP链氏求导法则：

     

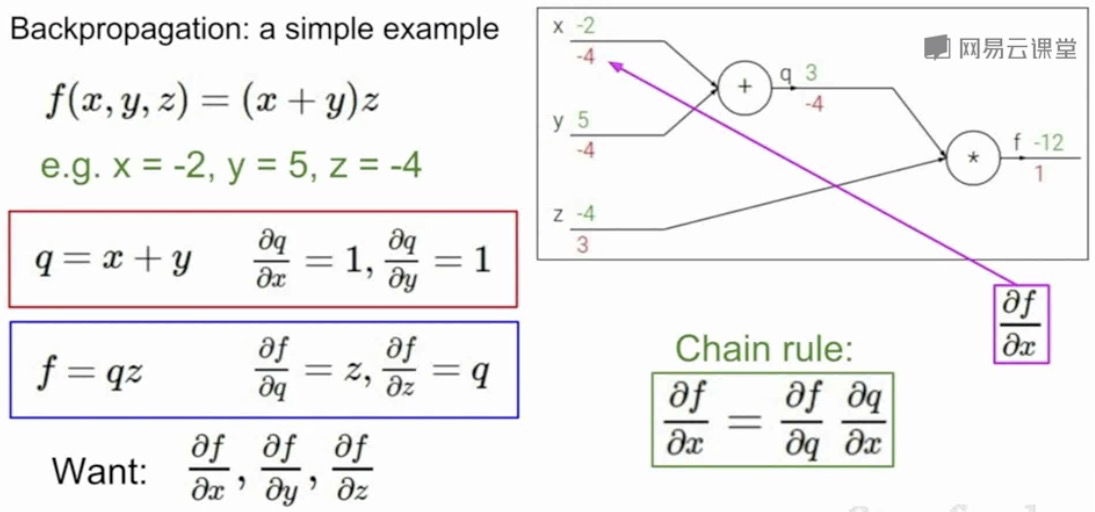
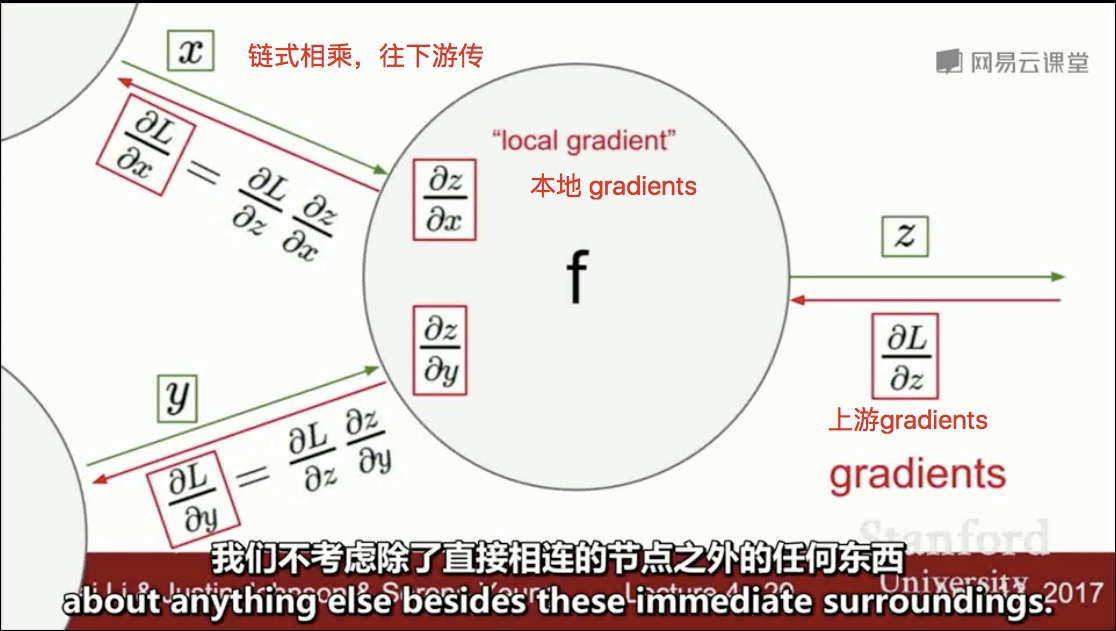
    -->上图像AST一样拆得太细了，能否做相应的组合，合并一些简短的公式“模板”，推导出解析表达式，减小中间内存占用？
  • 相关阅读:
    PHP实现发送模板消息（微信公众号版）
    laravel 跨域问题
    微信授权登录
    支付demo2
    支付demo1
    微信支付注意点
    微信支付方式区分
    debian，dietpi，linux中文乱码解决方法
    嵌入式应该深入专研STM32还是继续学习linux内核驱动呢？
    arduino下载ESP8266开发板的方法
  • 原文地址：https://www.cnblogs.com/cx2016/p/13080431.html
Copyright © 2011-2022 走看看