GCN 为什么是低通滤波器?具体在干啥?
· 前言
学过信号与系统 + 通信原理的同学应该对卷积、滤波、频率、傅里叶变换这些名词有很深的感情吧。。。前一段时间听了图神经网络研讨会的报告后,想简单介绍下 GCN 中卷积、滤波等概念的理解,再者最近看了台大的相关课程觉得讲的非常好,也摘抄一些分享给大家。
本文脉络
- 卷积、滤波、频率的直观理解
- 基于 "基" 的信号合成与分解
- 图网络的谱分析
- 图卷积有什么问题
- ChebNet 与 GCN
01
—
卷积、滤波、频率的直观理解
卷积这个概念可能有些人是从 CNN 这里才了解的,但其实卷积作为一种运算在诸多工程领域有着很久远的应用历史。卷积操作有时候也会被称为滤波操作,顾名思义就是过滤掉信号中的某些成分 (某些频率的波)。上面这句话隐含了 3 个意思:1)时域 / 空域信号可以转化成频域信号;2)信号在频域可以分解成多个频率的波;3)卷积可以对特定频率的波做处理。
以图片处理为例,争取不用公式让大家直观理解上面 3 句话。
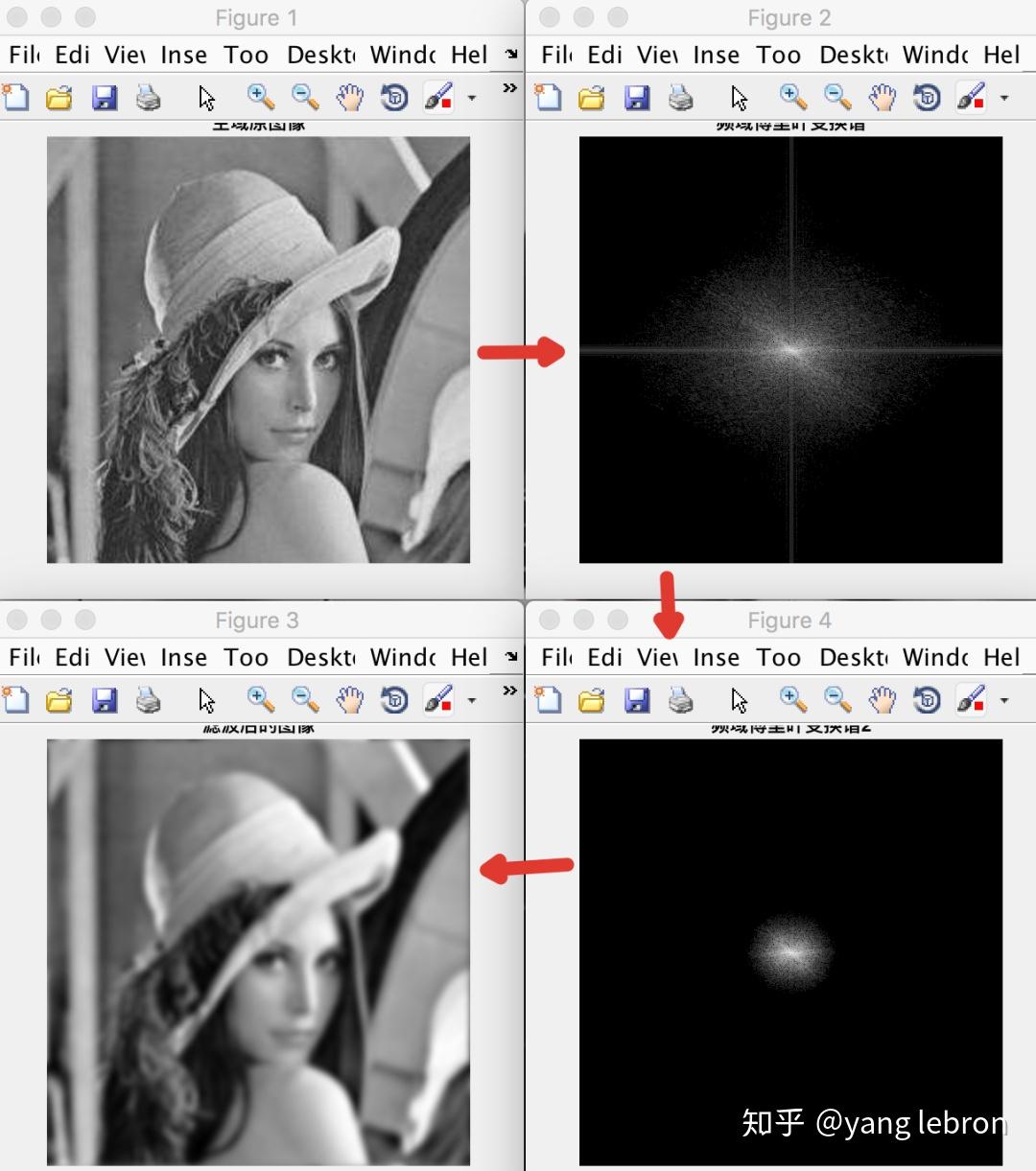
上面 4 张图是随手跑的 matlab 的结果。图 1 是原始 lena,是我们肉眼可以理解的空域信号。图 2 是将图 1 进行二维傅里叶变换后的频谱图,是我们肉眼无法直观理解的频率域信号的可视化结果。越靠近频谱图中心位置信号频率越低,即中心位置的信号是低频信号,对于空域图 1 中的像素变化很 "慢" 的光滑部分比如脸部皮肤和肩部。远离中心位置的信号是高频信号,对应图 1 中的头发、帽檐等变化 "很快" 的部分。
我们使用一个频域低通滤波器把图 2 中高频部分都过滤掉得到图 4 的频谱图(除了中心低频被保留,其余高频全部过滤),这个频域操作等价于在图 1 这个空域信号上,用对应的卷积函数进行卷积操作。频率过滤得到图 4 后,再使用傅里叶逆变换回到空间域图 3,我们发现图 3 中高频纹理细节都没有了,剩下的低频光滑的内容。不同频率对应着不同强弱的能量。
从上面的例子我们发现,空间域的信号即一直图片,可以分解成频域不同频率的信号(不同频率的波)叠加,我们在频域对某些频率的信号进行处理,会反应到空域上相对应的原始信号上,等价于直接在空间域进行卷积操作。(一不小心,卷积定理都讲完了)
有图像背景的同学肯定知道,在 CNN 火起来之前都是使用一些专门的滤波器去卷积图片得到人为定义的特征,比如用 Gabor 滤波器得到纹理特征。还有更直观的,sobel 算子去卷积一张图片得到边缘信息,如下左图转灰度后再和 sobel 滤波器卷积一下就提取出右边的图。

因此,卷积给我们的感觉是,可以提取一类特定的特征信号,比如边缘特征、高频纹理特征等等。但是 CNN 是很多层的,提取了一层特征后的 feature map 上再来一次卷积得到的是什么特征呢?还有 GCN 这类非图像数据,又该如何理解这个提取的特征信号的?
02
—
基于 "基" 的信号合成与分解
世界是稀疏的。比如任何一张图像都可以用一组固定的小图像块叠加而成。这里其实是在时域找到一组基(一组固定的小图像块)来分解信号(图片)。

更有趣的是,这组基并不唯一。如上图所示,可以是左边这样的一组 DCT(离散余弦变换) 基;也可以是用 dictionary learning 学习出来的中间这样的一组基;不同组基向量的大小也是可以不同的,如右边小图像块的大小可以不同。
上面的这组基是时域的,而我们要讲的 GNN 谱分析是从频域来分解的,不过原理都是类似的。下图是时域的一个方波信号,那么对应到频域就可以分解成各个不同频率和幅值的正弦波。(如果你用过示波器,这个过程就很好理解)
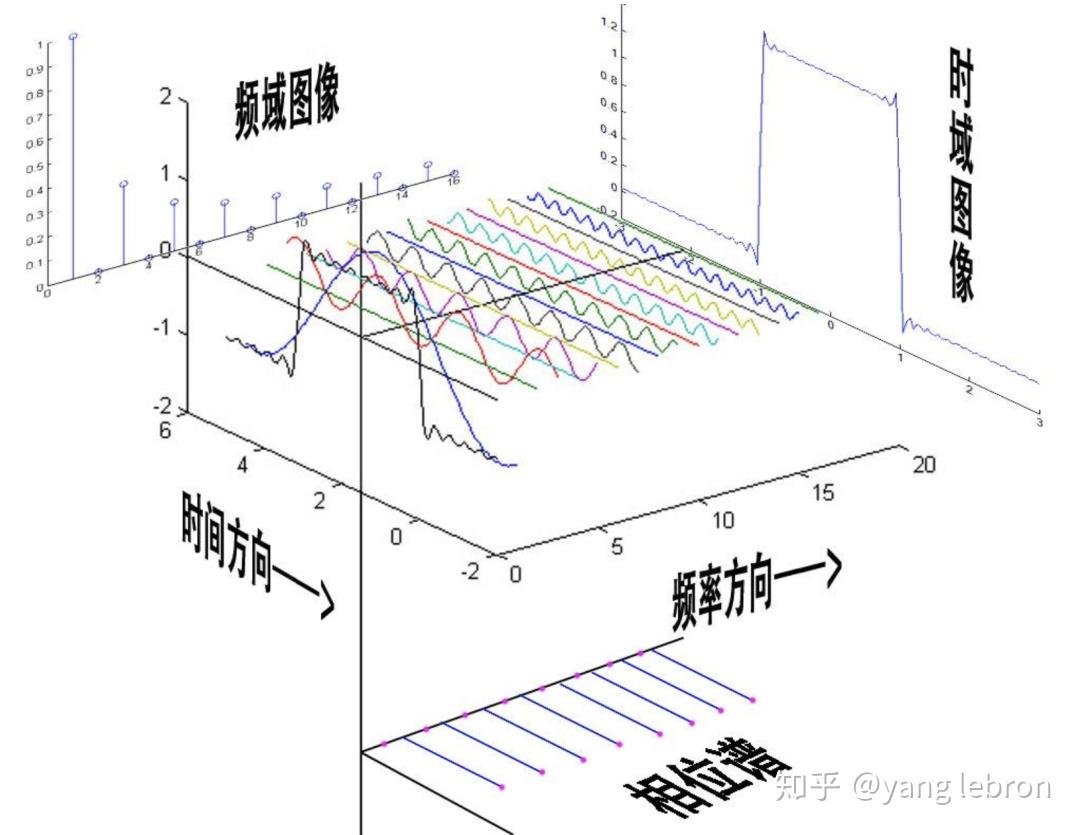
一个时域的信号,被我们分解成不同频率(不同能量)的信号叠加,有 DC 直流部分、有能量很高的波、有能量很弱的波。

上图展示了一个信号,分别从时域分解和频域分解的 2 种情况。其中 和 分别表示一组基向量,一般我们都会选择一组单位正交基来合成信号。
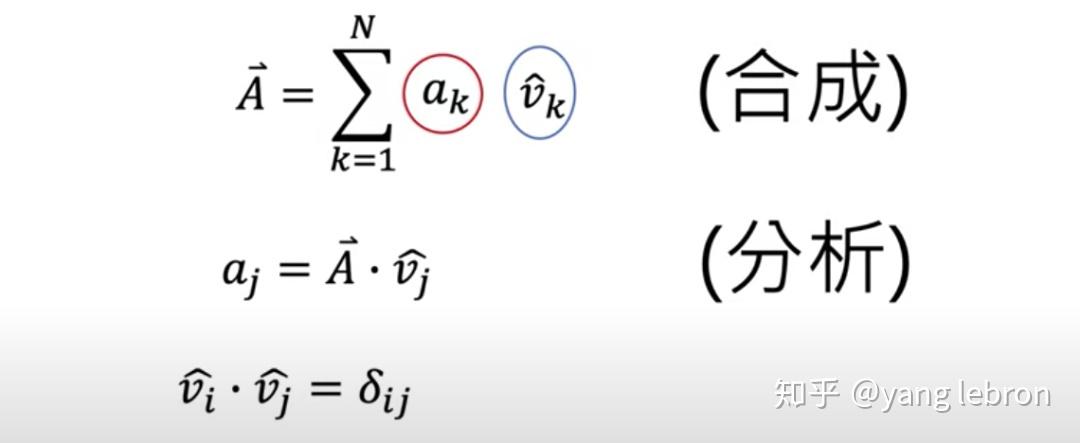
选定了基后,如果我们想要知道在某个基(某个频率)上的信号大小,则利用上图的分析过程来求的,一个内积即可。
最常用的就是傅里叶这套了,如下图所示,其中 就是基。
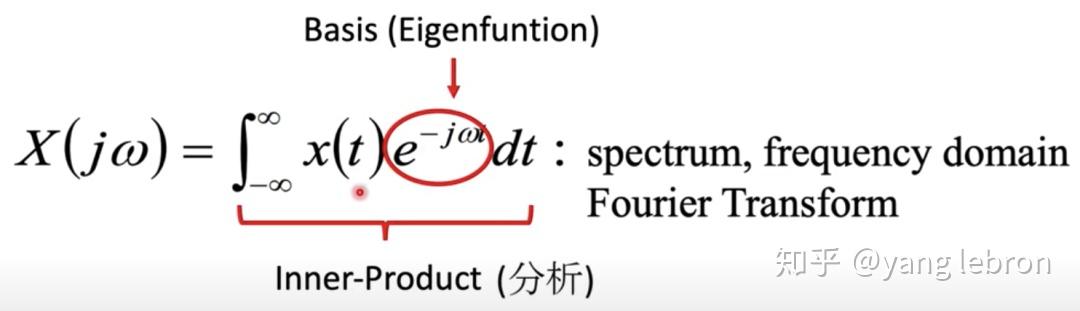
有了上面这些知识,就可以正式开始分析 GCN 了。。。
03
—
图网络的谱分析
在介绍图卷积之前,还得从普通卷积讲起,首先介绍一维连续卷积的定义,f 和 g 的卷积定义如下,附上几乎每个老师上课都用过的动图:
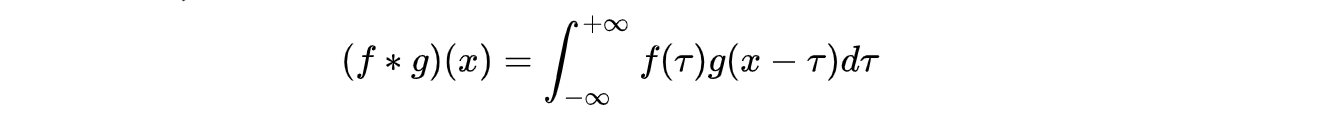
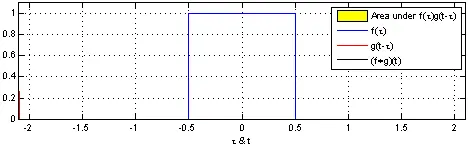
实际应用中,我们更多的是处理二维离散信号,二维离散卷积定义如下:
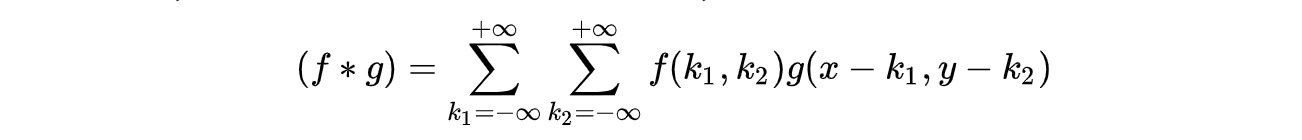
简单概括卷积过程就是:旋转、平移、相乘、求和。可以看出卷积运算是很复杂的,所以有没有办法不去直接求卷积呢?
这里就要介绍一个前面提过的定理,卷积定理:函数卷积的傅里叶变换等于函数傅里叶变换的乘积。可见对函数傅里叶变换后的乘积在进行傅里叶逆变换就可以得到原始函数的卷积。
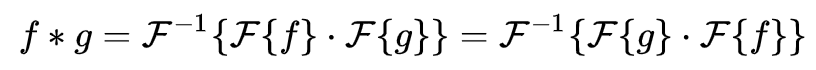
上式中
代表傅里叶变换
表示傅里叶逆变换。
回到图网络上,时域的卷积不仅计算难,连定义一个卷积核都难。因此也是依靠卷积定理,在频域来做些骚操作,下图所示:
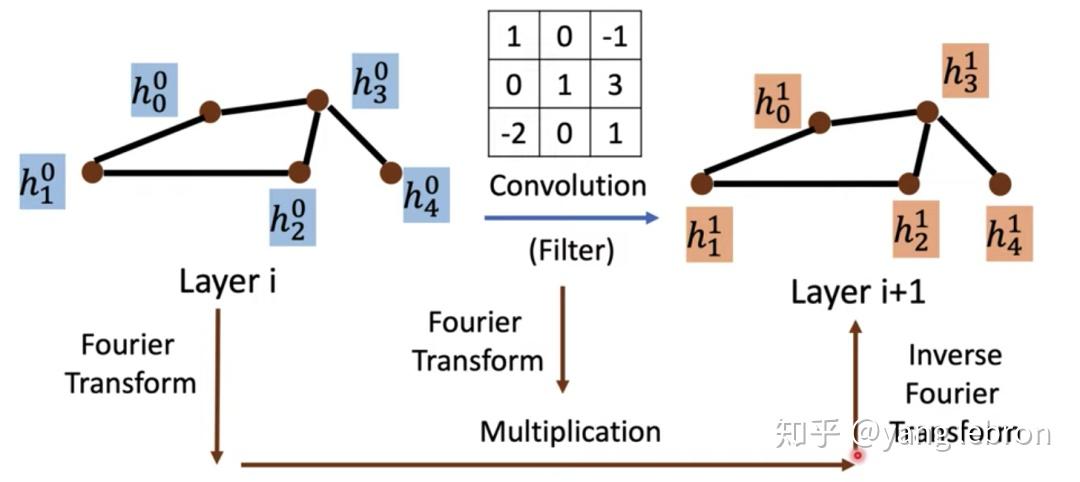
现在我们目标就是定义好图傅里叶变换和逆变换即可!
类比普通的傅里叶变换就是求信号在
上的投影,那么图傅里叶变换也是求信号 x 在一组正交基 上的投影。 图傅里叶变换如下:

上表来自知乎网友文章截图
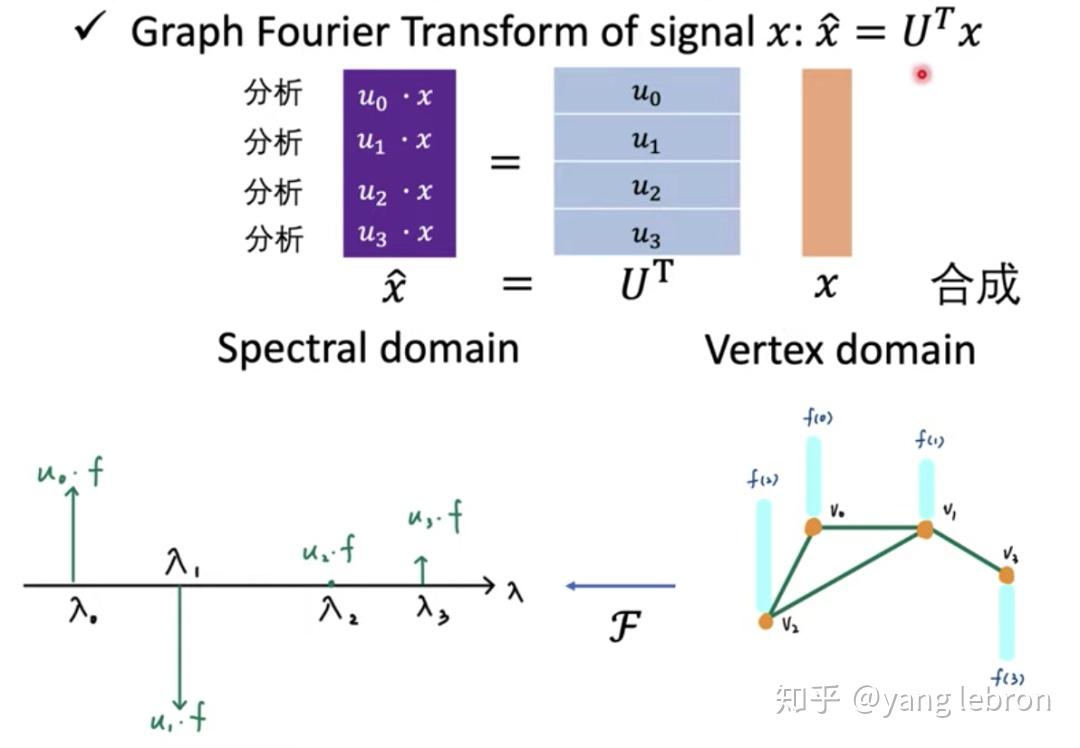
那么上图中的这组基
从哪里来呢?分析得到的特征值
又是什么意思呢?
关于
,特征值 / 特征向量听名字就知道很有用是不是,都叫特征了,肯定是能代表信号的属性的。学过线性代数的都很熟悉,就不啰嗦了。直接来说这组傅里叶基
怎么求。

先约定下关于图网络的符号表示。对于一个 graph 网络 G,那么可以用节点 V (N 个),和边 E 来表示。对于任意一个网络,可以得到 2 个矩阵 A 和 D。邻接矩阵 A 的定义是表示如果 2 个节点有边关联则未 1,否则未 0. 度矩阵 D 的定义是该节点的度数(对角阵)。
有了 A 和 D,就可以计算出网络 G 的拉普拉斯矩阵:L = D-A。

网络的拉普拉斯矩阵 L 是一个对称的半正定矩阵,可以分解成
的形式。并且这里的
就是我们想要的傅里叶变换的基,
就是信号的特征频率。
到此,我们就可以用利用卷积定理和图傅里叶变换得到图卷积的解法了:
图信号 f 和 g 的图卷积,类比普通信号 f 和 g 的普通卷积,形式是一样的。
参考第一小节的图片滤波,那么对于一个图信号 x,也是先做傅里叶变换到频域
,然后在频域进行滤波即和同样傅里叶变换后的滤波器
进行乘积得到
;最后再傅里叶逆变换回去即得到时域得结果 y=
。
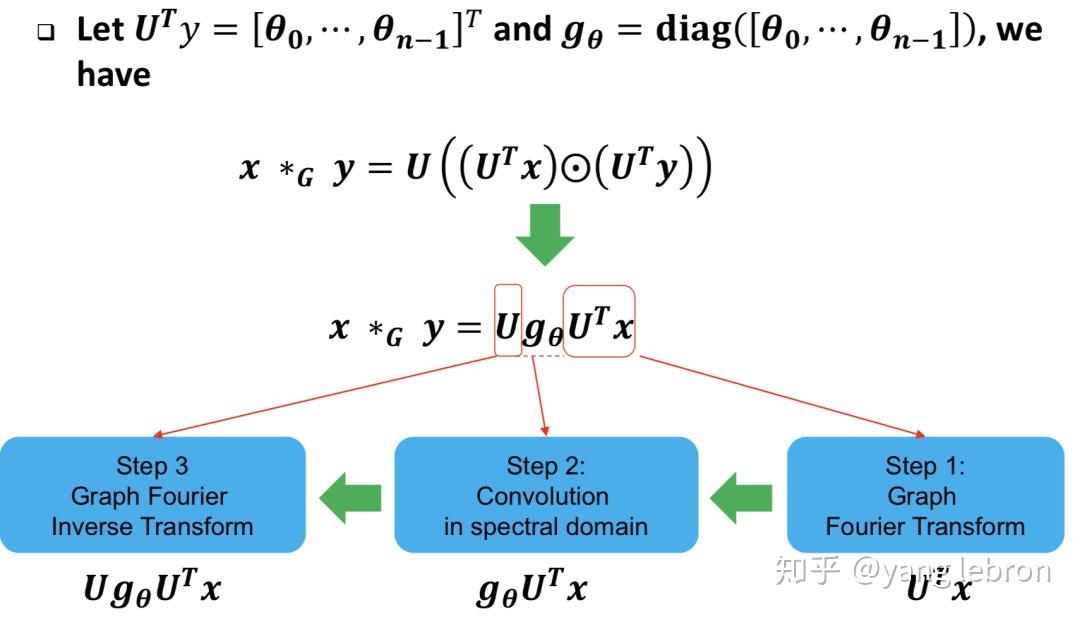
画成矩阵的形式就是下面这样:
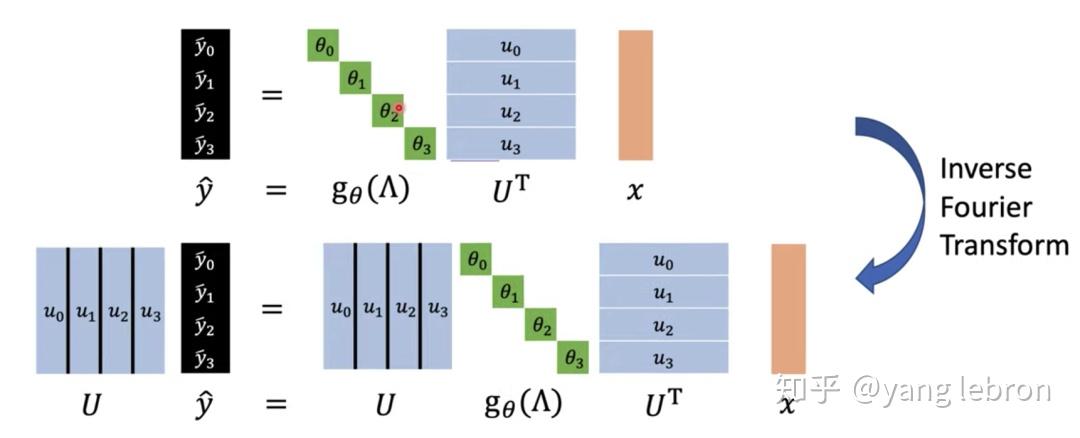
为了更加直观一点,我们进一步变换一下,把前面介绍的拉普拉斯矩阵 L 再引入回来:
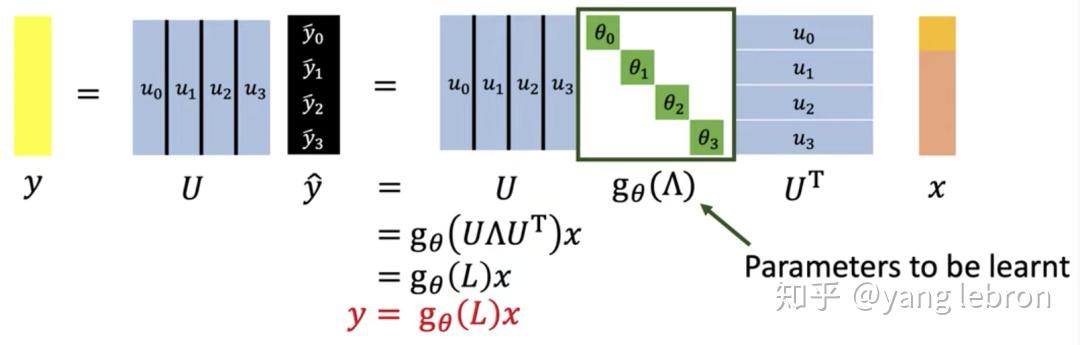
所以图卷积计算,相当于就是拿拉普拉斯矩阵 L 的函数来对信号进行一个处理!这个函数的参数也就是我们的卷积核参数,模型需要学习的参数。这个处理会做些啥呢,和低通滤波器又有什么关系呢?
04
—
图卷积有什么问题
复用一个台大课程上具体的例子来说明下拉普拉斯矩阵 L 的函数在图 graph 上操作的过程。
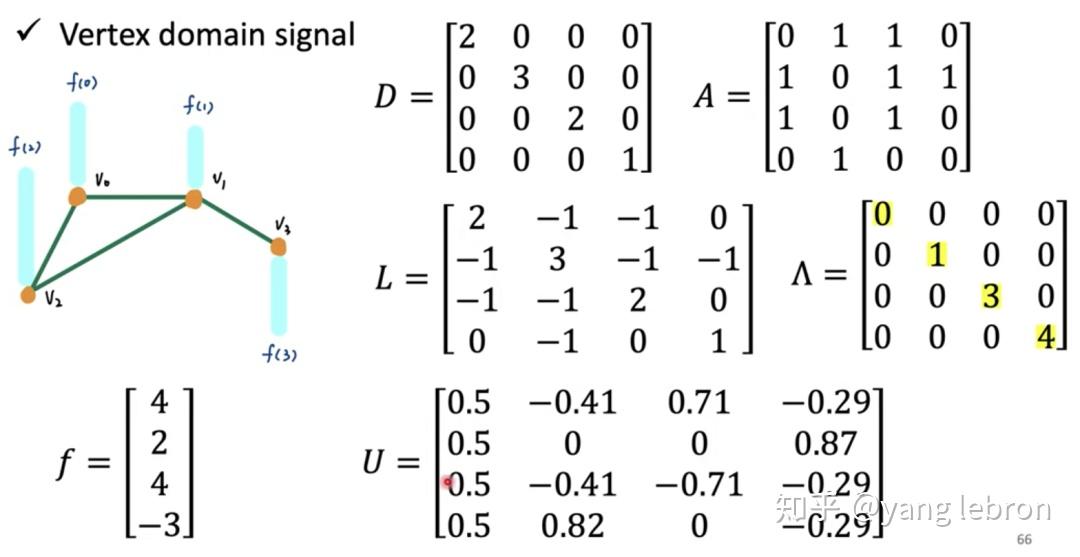
上面定义了一个简单的图网络信号 f,共有 4 个节点,每个节点就一维数值。那么这个 graph f 的度矩阵 D 和邻接矩阵 A,以及拉普拉斯矩阵 L 和对应的分解结果如上所示(上图矩阵 A 写错了)。
用最简单的拉普拉斯 L 的函数
来作用到这个图 f 上,得到结果 Lf 是如下:
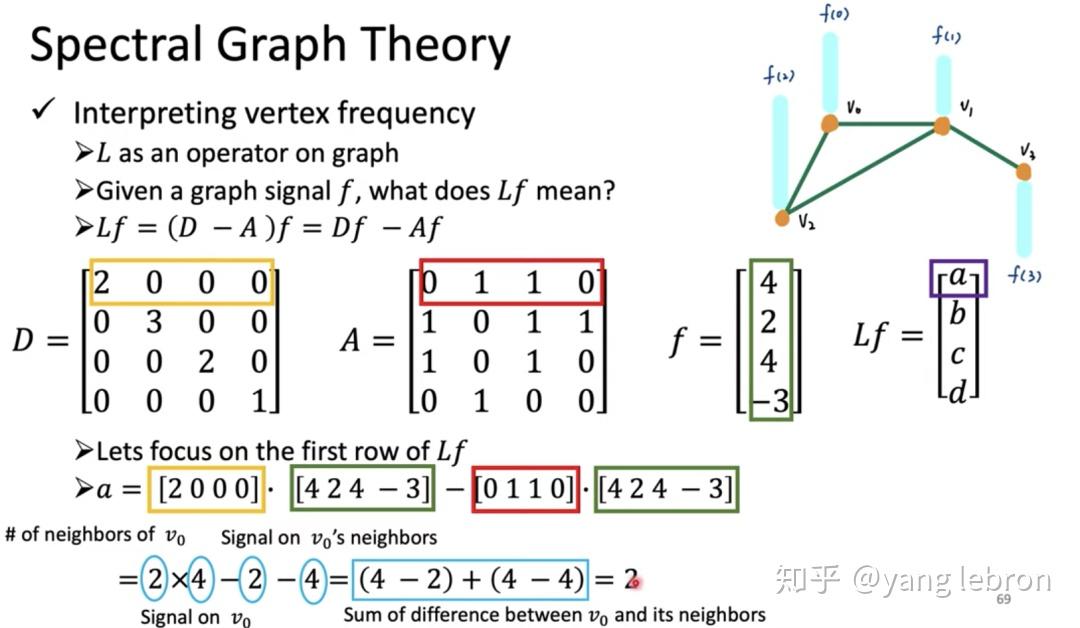
仔细看上面的计算过程,当计算 Lf 的第一个值 a 时, a=(4-2) + (4-4); 可以从参与计算的数值(黄色框、红色框、军绿色框中数值)看出,第一项 (4-2) 中的 4 代表 v0 节点的信号大小 4,其中的 2 代表 v1 的信号大小;第二项(4-4)中的第一个 4 代表 v0 节点信号大小,第二个 4 代表 v2 节点信号大小。之所以是有 2 项是因为 v0 节点的度 = 2,即有 2 个邻居(v1 和 v2)。
有没有总结出规律!当用 L 作用到图 f 上时,某种程度上可以看作是计算节点信号与自己邻边节点信号的差值。这个差值的大小变化程度是不是就类似于第一小节说的图片像素的差距,差距变化越快就是高频,反之则代表低频。
再思考一个问题,上面计算过程发现,当我们计算第一个节点 v0 时,只用到了邻居 v1 和 v2 的值,没有用到 v3,因为 v0 和 v3 直接没有边。下图矩阵直观的看出当
时,这个函数作用的 f 上,求 y 第一行 的 2 时,由于 L[0][3]=0, 代表和 v3 节点没有邻边,所以用不到 v3 节点的信息。
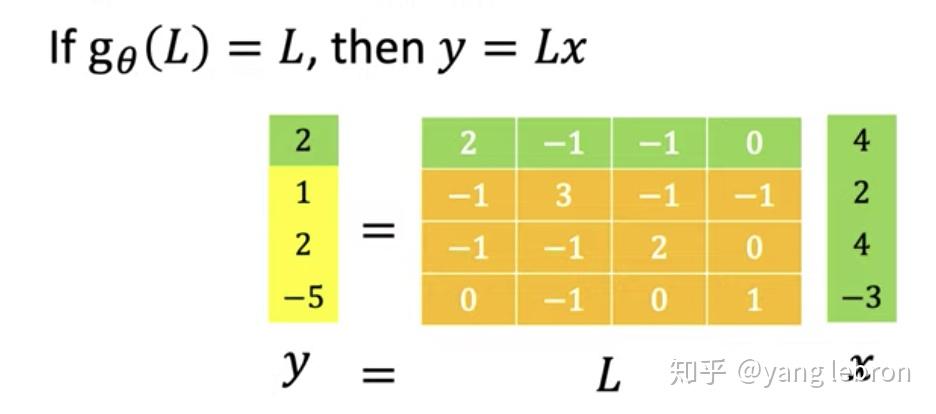
这样肯定是有信息损失的,相当于我们每次更新一个节点时,只用了 1 阶邻居节点的信息。如果我们的函数再复杂点呢,比如取 2 次方
。
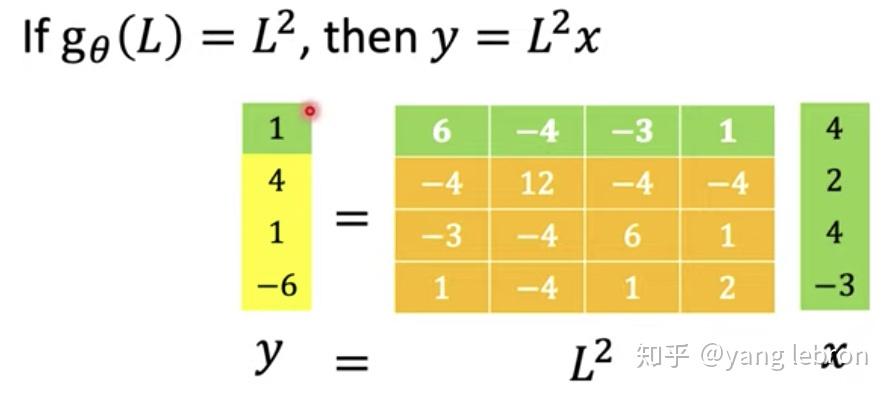
此时可以看出 L 的函数包含其 2 次方项后,矩阵中都是非 0 项,则更新节点 v0 时,v3 节点的信息也会被用到。因为 v3 和 v0 虽然不是直接邻居,但是他们存在着 2 阶邻边,所以当
时,更新某一个节点时会用到其所有 2 阶邻居的信息。
讲到这里就引出当前 graph 卷积的几个问题。
1)卷积函数
中包含 L 的 M 次方,更新节点时就会用到它的 M 阶邻居。比如
时,其中就包含了 N 次方,那么更新任何一个节点时,都需要用到所有节点信息,这个显然是不合理也不现实的,N 很大时没法算了,这种性质称为非 localize,Nonlocal 的。对比图像卷积,每个值就只和卷积核大小内的像素有关。所以 graph 卷积这样不具备 localize 特性。
2)前面提到学习图卷积的参数就是
,这个参数个数是 N,即和图的节点个数有关,每增加一个节点,这个参数就要变化。
3)需要对 L 进行矩阵分解,大矩阵的矩阵分解计算量是非常庞大的。
05
—
ChebNet 与 GCN
讨论上面几个问题,就必须要提 ChebNet 这个里程碑工作了。
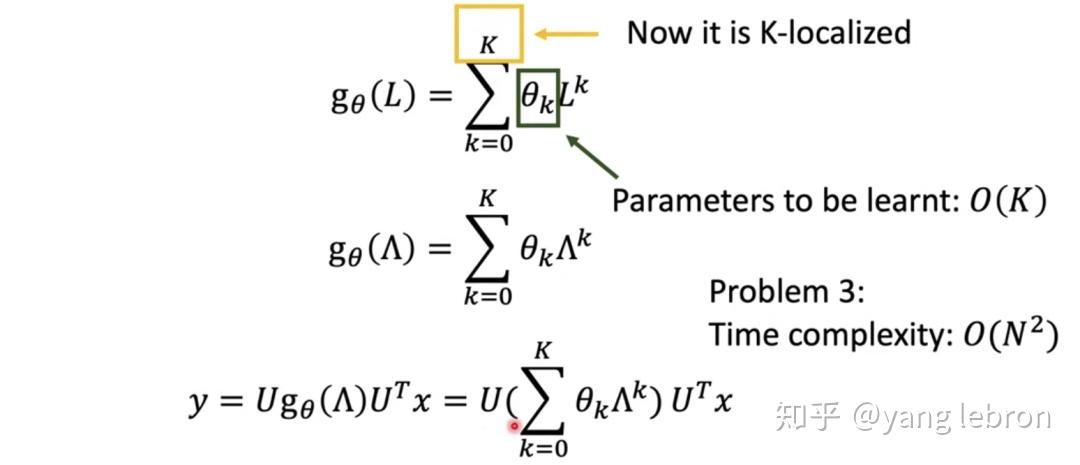
ChebNet 简单解释就是用切比雪夫多项式拟合 L 的 K 次多项式作为卷积函数。如上图公式所示,这样设计后,每个节点更新就最多和 K 阶邻居有关,实现了 localize。 同时参数个数也定死是 K 个,不会随着 graph 的变化而变化。拟合的过程如下:
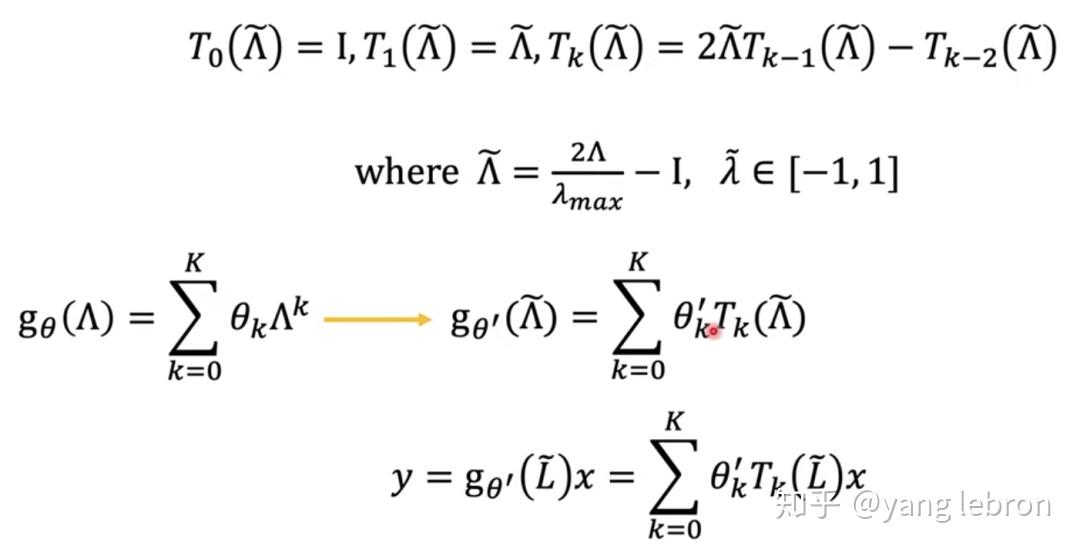
最终得到的卷积公式就是上式 y 的计算过程,这样处理后,计算量就下来了,从 O(N*N) 变成 O(KE):
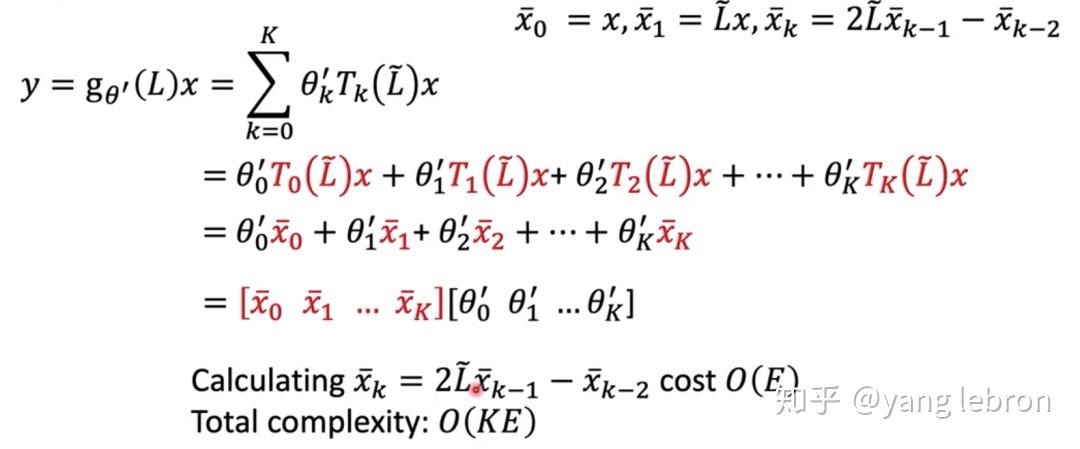
原理有点类似下面的函数求问题 (2) 时用变换后的多项式分解来求解会简化计算。(这个变换我也没深入推导过)

用了 ChebNet 后,上一小节的 3 个问题就都解决了。使用广泛的 GCN 就是 ChebNet K= 1 时的一阶近似。

上面推导依赖几个思路:1)最大的特征值
比 2 略小,约等于 2. 2) 这里的拉普拉斯矩阵 L 可以正则化为:
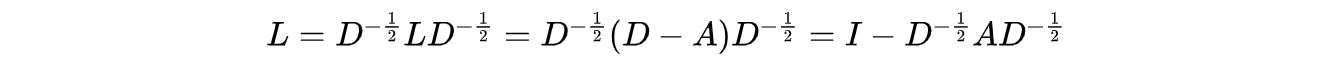
3)参数
的关系是人为设定的,不是理论。renormalization trick 也是作者这么定义的一个计算方法。其中
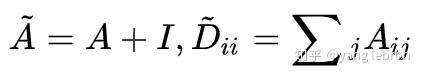
, A 相当于加了一次自己。
同时可以看到上面的特征值范围是 [-1,1], 那么在频率进行滤波时,即频率响应函数的范围也是在这范围内,属于低频段,所以 GCN 可以看作是一个低通滤波器。
经过上图变换后得到了最终网络下一层的输出
的计算方法。如果觉得这个式子不好理解,可以换成下面的形式:
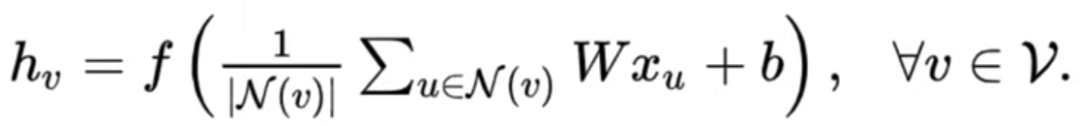
就是讲输入特征 x 经过一次变化 W 后,再将所有邻居(包括自己)的这些值求和相加,再求均值,最后经过一次 "激活" 函数 f,得到输出。这个式子理解起来就很传统了。
GCN 的效果如何,存在什么问题?关于这个,网上有很多资料,我就不介绍了,简单说即是经过多层后,有 over-smoothing 问题。效果的话,一般般吧,至少在很多图片任务上,效果非常差。在实际工作中,很少会直接用这么单纯的 GCN 的,应用较广的还是 graphsage、gat 这些。

写的真的太好了!! 理论一直有块搞不懂!! 蟹蟹!
非常棒
这里的 A 必须是 0,1 矩阵么?有权图怎么办呢?
A 就是邻接矩阵啊,有权值套进去就好了
如果是负权的话,拉普拉斯矩阵就不是正定的了,那就没法用
很棒的回答
请教一下,通过上述分析得出 GCN 是一个低通滤波器,那输入的信号 x 的频率怎么求?还有如何根据输入 x 的频率分布来设计合适的卷积核?
全文完