&【08】Python 数据类型之set

本文参考：

纯洁的微笑：http://www.ityouknow.com/python.html

Python 也包含有 集合 类型。集合是由不重复元素组成的无序的集。它的基本用法包括成员检测和消除重复元素。集合对象也支持像 联合，交集，差集，对称差分等数学运算。

集合结构如下：

# 集合结构如下：
set1 = {'hello', 'hello', 'word', 'word'}
print(set1)  # 输出 {'word', 'hello'}
# 　输出结果实现自动去重

1、集合创建

可以使用大括号 { } 或者 set() 函数创建集合，

创建格式：

parame = {value01,value02,...}
或者
set(value)

==注意：创建一个空集合必须用 set() 而不是 { }，因为 { } 是用来创建一个空字典。==

# 创建空集合
empty_set = set()
print(type(empty_set))  # 输出 <class 'set'>

# 创建空字典
empty_dict = {}
print(type(empty_dict))  # 输出 <class 'dict'>

2、集合的基本操作

2.1 添加元素

语法格式：

set.add(value)

将元素 x 添加到集合 s 中，如果元素已存在，则不进行任何操作。

s = set(('hello', 'world'))
# 另一种创建集合方式
# s = {'hello', 'world'}
print(s)  # 输出 {'world', 'hello'}

# 向集合 s 中添加元素
s.add('!')
print('添加元素后：%s' % s)  # 输出 添加元素后：{'!', 'world', 'hello'}

除了 add() 方法可以添加元素外，还有一个方法，也可以添加元素，并且参数可以是列表，元组，字典等，语法格式如下：

set.update(value)
set.update(value,value)

参数 x 可以是一个，也可以是多个，多个参数之间用逗号相隔

s = {5}
# 　1）添加列表
s.update([1, 3], [2, 4])
print('添加元素后的集合是：%s' % s)  # 输出 {1, 2, 3, 4, 5}

# 2）添加元组
s.update(('h', 'j'))
print('添加元素后的集合是：%s' % s)  # 输出 添加元素后的集合是：{'j', 1, 2, 3, 4, 5, 'h'}

2.2 移除元素

语法格式如下：

set.remove(value)

将元素 x 从集合 s 中移除，如果元素不存在，则会发生错误。

s = {2}
# 将元素 2 从集合中移除
s.remove(2)
print('移除元素 2 后的集合是：%s' % s)  # 输出 移除元素 2 后的集合是：set()

# 如果移除集合中不存在的元素会报异常
s.remove('hi')

# 　异常信息
Traceback (most recent call last):
   File "main.py", line 20, in <module>
   s.remove('hi')
   KeyError: 'hi'

此外还有一个方法也是移除集合中的元素，且如果元素不存在，不会发生错误。格式如下所示：

s = {1}
s.discard(2)
thisset = set(("Google", "Runoob", "Taobao"))
# 不存在不会发生错误
thisset.discard("Facebook") 
print(thisset) # 输出 {'Taobao', 'Google', 'Runoob'}

我们也可以设置随机删除集合中的一个元素，语法格式如下：

set.pop()

s = {1, 2, 3, 4, 5}

# 随机删除集合中的一个元素
# pop()会返回移除的元素本身
print(s.pop())  # 输出 1
print('移除元素后的集合是：%s' % s)  # 输出 {2, 3, 4, 5}

注意：在交互模式，pop 是删除集合的第一个元素（排序后的集合的第一个元素）。

2.3 计算集合元素个数

语法格式如下：

len(set)

计算集合 s 元素个数。

s = {1, 2, 3}
print('集合 s 的长度是：%s' % len(s)) 
# 输出 集合 s 的长度是：3

2.4 清空集合

语法格式如下：

set.clear()

清空集合 s

s = {1, 2, 3}
s.clear()
print('集合清空后的结果是：%s' % s)
# 输出 集合清空后的结果是：set()

2.5 判断元素是否存在

语法格式如下：

value in set

判断元素 x 是否在集合 s 中，存在返回 True，不存在返回 False。

s = {'hello', 'word'}
# 判断元素 hello 是否在集合 s 中
print('hello' in s) # 输出结果：True

2.6 集合运算

集合之间的运算符分别是-、|、&、^ ; 下面以两个集合之间的运算为例进行讲解：

• -：代表前者中包含后者中不包含的元素
• |：代表两者中全部元素聚在一起去重后的结果
• &：两者中都包含的元素
• ^：不同时包含于两个集合中的元素

a = set('ABCDEF')
b = set('DEFGHJ')
print(a)  # 输出 {'C', 'E', 'F', 'D', 'A', 'B'}
print(b)  # 输出 {'G', 'H', 'D', 'E', 'J', 'F'}

# 集合a中包含而集合b中不包含的元素
print(a - b)  # 输出 {'C', 'A', 'B'}

# 集合a或b中包含的所有元素
print(a | b)  # 输出 {'B', 'G', 'H', 'C', 'A', 'D', 'E', 'J', 'F'}

# 集合a和b中都包含了的元素
print(a & b)  # 输出 {'F', 'D', 'E'}

# 不同时包含于a和b的元素
print(a ^ b)  # 输出 {'A', 'G', 'B', 'H', 'C', 'J'}

3、集合推导式

和列表一样，集合也支持推导式

# 判断元素是否存在
a = {x for x in 'abcedf' if x not in 'abc'}
print(a)  # 输出 {'r', 'd'}

4、集合内置方法

4.1 difference()

difference()方法用于返回集合的差集，即返回的集合元素包含在第一个集合中，但不包含在第二个集合(方法的参数)中，返回一个新的集合。

difference() 方法语法：

set.difference(set)

实例：

两个集合的差集返回一个集合，元素包含在集合 x ，但不在集合 y ：

x = {"apple", "banana", "cherry"}
y = {"google", "microsoft", "apple"}

# 求两个集合的差集，元素在 x 中不在 y 中
z = x.difference(y)

print('两个集合的差集是：%s' % z)  # 输出 {'banana', 'cherry'}

4.2 difference_update()

• difference_update()方法用于移除两个集合中都存在的元素。
• difference_update() 方法与 difference() 方法的区别在于 difference() 方法返回一个移除相同元素的新集合，而 difference_update() 方法是直接在原来的集合中移除元素，没有返回值。

x = {"apple", "banana", "cherry"}
y = {"google", "microsoft", "apple"}
x.difference_update(y)
print(x)  # 输出 {'banana', 'cherry'}

x1 = {1, 2, 3, 4}
y1 = {1, 2, 3}
x1.difference_update(y1)
print(x1)  # 输出 {4}

4.3 intersection()

intersection()方法用于返回两个或更多集合中都包含的元素，即交集，返回一个新的集合。

intersection() 方法语法：

set.intersection(set1, set2 ... etc)

参数：
set1 -- 必需，要查找相同元素的集合
set2 -- 可选，其他要查找相同元素的集合，可以多个，多个使用逗号 , 隔开

实例：

# 返回两个或者多个集合的交集
x = {"apple", "banana", "cherry"}
y = {"google", "runoob", "apple"}
z = x.intersection(y)
print(z)  # 输出 {'apple'}

# 　返回三个集合的交集
x = {"a", "b", "c"}
y = {"c", "d", "e"}
z = {"f", "g", "c"}

result = x.intersection(y, z)
print('三个集合的交集是：%s' % result)  # 输出 {'c'}

4.4 intersection_update()

• intersection_update() 方法用于获取两个或更多集合中都重叠的元素，即计算交集。
• intersection_update() 方法不同于 intersection() 方法，因为 intersection() 方法是返回一个新的集合，而 intersection_update() 方法是在原始的集合上移除不重叠的元素。

intersection_update() 方法语法：

set.intersection_update(set1, set2 ... etc)

参数
set1 -- 必需，要查找相同元素的集合
set2 -- 可选，其他要查找相同元素的集合，可以使用多个多个，多个使用逗号‘,’ 隔开

实例：

# 返回一个无返回值的集合交集
x = {"apple", "banana", "cherry"}
y = {"google", "runoob", "apple"}
x.intersection_update(y)
print(x)  # 输出 {'apple'}

x = {"a", "b", "c"}
y = {"c", "d", "e"}
z = {"f", "g", "c"}
x.intersection_update(y, z)
print(x)  # 输出 {'c'}

4.5 union()

union() 方法返回两个集合的并集，
即包含了所有集合的元素，重复的元素只会出现一次，返回值返回一个新的集合

语法：

set.union(set1, set2...)

参数
set1 -- 必需，合并的目标集合
set2 -- 可选，其他要合并的集合，可以多个，多个使用逗号 , 隔开。

实例：

# 合并两个集合，重复元素只会出现一次：
x = {"apple", "banana", "cherry"}
y = {"google", "runoob", "apple"}
z = x.union(y)
print(z) # 输出 {'cherry', 'banana', 'google', 'apple', 'runoob'}

# 合并多个集合：
x = {"a", "b", "c"}
y = {"f", "d", "a"}
z = {"c", "d", "e"}
result = x.union(y, z)
print(result) # 输出 {'a', 'e', 'b', 'f', 'c', 'd'}

4.6 isdisjoint()

isdisjoint() 方法用于判断两个集合是否包含相同的元素
==如果没有返回 True，否则返回 False。==

语法：

set.isdisjoint(set)

实例：

x = {"apple", "banana", "cherry"}
y = {"google", "runoob", "apple"}
# 　判断集合 y 中是否包含集合 x 中的元素，如果没有返回 True, 有则返回 False
z = x.isdisjoint(y)
# 结果返回 False,说明集合 y 中有和 x 中相同的元素
print(z)  # 输出 False

x = {"apple", "banana", "cherry"}
y = {"google", "runoob", "baidu"}
# 　判断集合 y 中是否包含集合 x 中的元素，如果没有返回 True, 有则返回 False
z = x.isdisjoint(y)
# 结果返回 True,说明集合 y 中没有和 x 中相同的元素
print(z)  # 输出 True

预备知识：子集与超集

子集

如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。

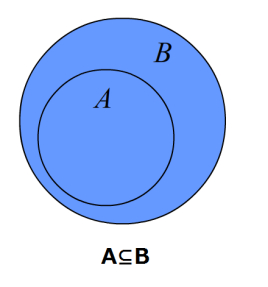
超集

定义：
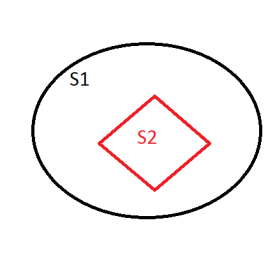
如果一个集合S2中的每一个元素都在集合S1中，且集合S1中可能包含S2中没有的元素，则集合S1就是S2的一个超集
反过来，S2是S1的子集。 S1是S2的超集，若S1中一定有S2中没有的元素，则S1是S2的真超集，反过来S2是S1的真子集

4.7 issubset()

issubset() 方法用于判断s1是否是s2的子集（判断集合s1的所有元素是否都包含在指定集合s2中）
如果是则返回 True，否则返回 False。

语法:

s1.issubset(s2)

判断s1是否为s2的子集

返回布尔值，如果是，返回 True，否则返回 False。

实例:

# 判断集合 x 的所有元素是否都包含在集合 y 中：
s1 = {"a", "b", "c"}
s2 = {"f", "e", "d", "c", "b", "a"}
z = s1.issubset(s2) # 判断s1是否为s2的子集
# True 说明 集合 x 中的元素都包含在 y 中
print(z)  # 输出 True

注意： 必须是集合s1中的元素都包含在s2内，否则结果为 False(子集)

# 　集合 y 中只有元素 b 和 c ，执行结果为 False
s1 = {"a", "b", "c"}
s2 = {"f", "e", "d", "c", "b", "y"}
z = s1.issubset(s2) # 判断s1是否为s2的子集
print(z)  # 输出 Flase

4.8 issuperset()

issuperset() 方法用于 判断s1是否为s2的超集 (判断指定集合s2的所有元素是否都包含在原始的集合s1中)
如果是则返回 True，否则返回 False。

语法：

s1.issuperset(s2)

判断s1是否为s2的超集*

返回布尔值，如果是，则返回 True，否则返回 False。

实例：

# 判断集合 y 的所有元素是否都包含在集合 x 中：
s1 = {"f", "e", "d", "c", "b", "a"}
s2 = {"a", "b", "c"}
z = s1.issuperset(s2) # 判断s1是否为s2的超集
print(z) # 输出 True 因为s1包含s2

# 如果没有全部包含返回 False：
s3 = {"f", "e", "d", "c", "b"}
s4 = {"a", "b", "c"}
z = s3.issuperset(s4) # 判断s3是否为s4的超集
print(z) # 输出 False 因为s3中没有‘a’

issubset()与issuperset()的区别

• 两者相反
  • issubset() 方法用于 判断s1是否是s2的子集
  • issuperset() 方法用于 判断s1是否为s2的超集

s1 = {"a", "b", "c"}
s2 = {"f", "e", "d", "c", "b", "a"}
z = s1.issubset(s2)  # 判断s1是否为s2的子集
print(z)  # 输出 True
m = s1.issuperset(s2)  # 判断s1是否为s2的超集
print(m)  # 输出 False

4.9 symmetric_difference()

symmetric_difference() 方法返回两个集合中不重复的元素集合，即会移除两个集合中都存在的元素，结果返回一个新的集合。

语法：

set1.symmetric_difference(set2)

实例：

# 返回两个集合组成的新集合，但会移除两个集合的重复元素：
x = {"apple", "banana", "cherry"}
y = {"google", "runoob", "apple"}
z = x.symmetric_difference(y)
print(z)  # 输出 {'google', 'banana', 'runoob', 'cherry'}

4.10 symmetric_difference_update()

symmetric_difference_update() 方法移除当前集合中在另外一个指定集合相同的元素，并将另外一个指定集合中不同的元素插入到当前集合中。(在原有集合上修改)

语法：

set1.symmetric_difference_update(set2)

实例：

# 在原始集合 x 中移除与 y 集合中的重复元素，并将不重复的元素插入到集合 x 中： （）
x = {"apple", "banana", "cherry"}
y = {"google", "runoob", "apple"}
x.symmetric_difference_update(y)
print(x)  # 输出 {'runoob', 'banana', 'google', 'cherry'}

4.11 其他

其他几个方法是对集合的增删改查，如：add() clear() copy() update() pop() remove() discard() 等方法，这些方法在对集合的基本操作章节有详解，大家到时候按需使用。