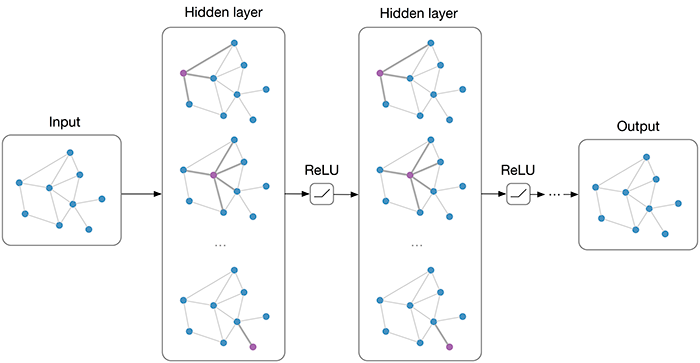
如何解决图神经网络（GNN）训练中过度平滑的问题？
12 个回答
泻药。
更正一下题目中的几个小误区：
原题：如何解决图神经网络（GNN）训练中过度平滑的问题？即在图神经网络的训练过程中，随着网络层数的增加和迭代次数的增加，每个节点的隐层表征会趋向于收敛到同一个值（即空间上的同一个位置）。
不是所有图神经网络都有 over-smooth 的问题，例如，基于 RandomWalk + RNN、基于 Attention 的模型大多不会有这个问题，是可以放心叠深度的～只有部分图卷积神经网络会有该问题。
不是每个节点的表征都趋向于收敛到同一个值，更准确的说，是同一连通分量内的节点的表征会趋向于收敛到同一个值。这对表征图中不通簇的特征、表征图的特征都有好处。但是，有很多任务的图是连通图，只有一个连通分量，或较少的连通分量，这就导致了节点的表征会趋向于收敛到一个值或几个值的问题。
注：在图论中，无向图的连通分量是一个子图，其中任何两个顶点通过路径相互连接。
为什么 GCN 中会存在 over-smooth 的问题
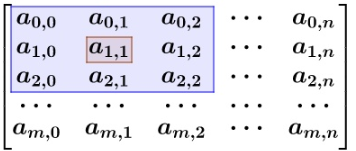
首先，回顾一下全连接神经网络和 Kipf 图卷积神经网络的公式：
其中， 为激活函数，
为节点特征，
为训练参数，
，
为邻接矩阵，
，
为图中的所有节点。可以发现图卷积神经网络只多了对节点信息进行汇聚的权重
。从
（无归一化）到
（归一化），再到
（对称归一化），对于该权重的研究已然汗牛充栋。
学有余力的同学可以往下看通式上 over-smooth 的证明，这里先以 为例，进行一个直观的解释：
首先，中间层的 由任务相关的
反向传播进行优化，可以理解为任务相关的模式提取能力，我们将其统一在图卷积后进行，多层卷积公式可以近似为：
其中， 可以看作被提取的多个隐藏层。化简该式：
其中，邻接矩阵的幂， 表示节点
和节点
之间长度为
的 walk 的数量。而它的度，
代表节点
到所有节点之间长度为
的 walk 的数量。
这时， 则代表以节点
为起点，随机完成
步的 walk 最后抵达节点
的概率。
随着 walk 步数的增多，远距离节点的抵达难度越来越小，被随机选中的概率越来越大。当 时，连通分量中的节点
到达连通分量中任意节点的概率都趋于一致，为
，其中
代表连通分量中节点的总数，即
，其中
、
代表连通分量的邻接矩阵和度矩阵。
令连通分量中的特征向量为 ，且
，
代表连通分量中节点的特征维度。节点信息的汇聚可以表示为：
连通分量中每个节点的特征都为所有节点特征的平均，也就是我们开始的时候说的，同一连通分量内的节点的表征趋向于收敛到同一个值。
补充说明：
这里的小把戏被
点名批评了："纵横试图给出理论上的证明，但是其回答中的证明有误，不能把矩阵的次幂运算拆解成元素的次幂运算，而且最后收敛于的猜想也不对。"
其实，当图稠密时，度矩阵一般会接近数量矩阵（当图为完全图时，度矩阵为数量矩阵），矩阵乘法满足交换率:
当图不稠密时，证明请参照 over-smooth 定理 部分叭～
另外有些小伙伴可能会误解，这里提醒一下：在完全图中，汇聚矩阵的值会收敛到 ，而特征向量会收敛到所有节点特征的平均，而不是
哦～
在感性地认识到图卷积与连通分量之间的关联后，有的工作想到利用特征分解（特征向量对应连通分量）给出 over-smooth 定理的证明[1]：
over-smooth 定理：假设图 由
个连通分量
构成，其中第
个连通分量可以用向量
表示：
那么，当图中不存在二分连通分量时，有：
其中， 和
表示线性组合
的系数，且：
本想写自己的证明过程，但由于篇幅较长喧宾夺主，有机会再贴～
试验与可视化
为了检验上述分析的正确性，更直观地理解 over-smooth 的过程，我们可以做一个小小的试验～ 感兴趣的同学可以使用 Jupyter 跑一下：
首先，定义三个连通子图：随机图（其实是一本书中的用例）、完全图和彼得森图：
import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline
subgraph_1 = nx.sedgewick_maze_graph()
subgraph_2 = nx.complete_graph(5)
subgraph_3 = nx.petersen_graph()
graph = nx.disjoint_union(subgraph_1, subgraph_2)
graph = nx.disjoint_union(graph, subgraph_3)
nx.draw_circular(graph)
plt.show()画出来是这样的：
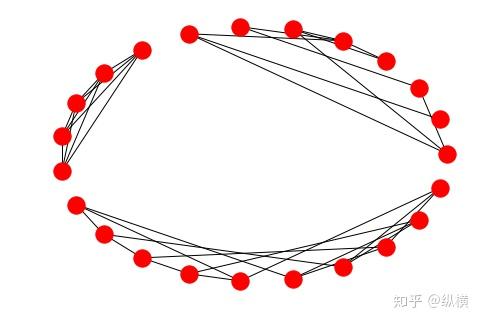图的三个连通子图：随机图、完全图和彼得森图
接着，计算汇聚矩阵 ，同学们也可以尝试其他的卷积核对比收敛过程：
import scipy
import scipy.sparse as sparse
nodelist = graph.nodes()
A = nx.to_scipy_sparse_matrix(graph, nodelist=nodelist, weight='weight', format='csr')
n, m = A.shape
diags = A.sum(axis=1).flatten()
with scipy.errstate(divide='ignore'):
diags_sqrt = 1.0 / diags
diags_sqrt[scipy.isinf(diags_sqrt)] = 0
DH = scipy.sparse.spdiags(diags_sqrt, [0], m, n, format='csr')
aggregate_matrix = DH.dot(A)最后，对汇聚矩阵 的
次幂进行可视化，这里使用 heatmap 可视化看起来效果还挺不错：
import seaborn as sns;
sns.heatmap(aggregate_matrix.todense())
aggregate_matrix = aggregate_matrix.dot(aggregate_matrix)
sns.heatmap(aggregate_matrix.todense())
...
for _ in range(5):
aggregate_matrix = aggregate_matrix.dot(aggregate_matrix)
sns.heatmap(aggregate_matrix.todense())得到的可视化结果如下：
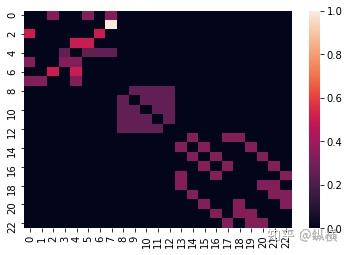1 次幂后矩阵的可视化
2 次幂后矩阵的可视化
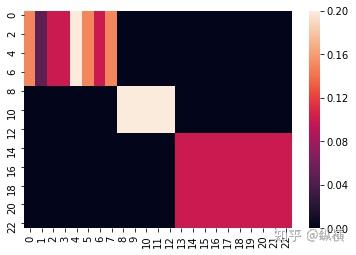10 次幂后矩阵的可视化
其中，图像的高和宽对应邻接矩阵的行和列，图像中像素的亮度表示邻接矩阵中对应元素值的大小。可以发现 随机图 的汇聚矩阵收敛到了几个常数，而 完全图和彼得森图 的汇聚矩阵收敛到了 。在与节点的特征矩阵相乘后，同一连通分量内的节点的表征会趋向于收敛到同一个值（连通分量内节点表征的加权平均）。特别的，当图为完全图时，节点的表征会收敛到分量内所有节点表征的平均。
如何解决 over-smooth 的问题
在了解为什么 GCN 中会存在 over-smooth 问题后，剩下的工作就是对症下药了：
图卷积会使同一连通分量内的节点的表征趋向于收敛到同一个值。
- 针对“图卷积”：在当前任务上，是否能够使用 RNN + RandomWalk（数据为图结构，边已然存在）或是否能够使用 Attention（数据为流形结构，边不存在，但含有隐式的相关关系）？
- 针对“同一连通分量内的节点”：在当前任务上，是否可以对图进行 cut 等预处理？如果可以，将图分为越多的连通分量，over-smooth 就会越不明显。极端情况下，节点都不相互连通，则完全不存在 over-smooth 现象（但也无法获取周围节点的信息）。
如果上述方法均不适用，仍有以下 deeper 和 wider 的措施可以保证 GCN 在过参数化时对模型的训练和拟合不产生负面影响。个人感觉，这类方法的实质是不同深度的 GCN 模型的 ensamble：
巨人肩膀上的模型深度 —— residual 等
Kipf 在提出 GCN 时，就发现了添加更多的卷积层似乎无法提高图模型的效果，并通过试验将其归因于 over-smooth：多层 GCN 可能导致节点趋同化，没有区别性。但是，早期的研究认为这是由 GCN 过分强调了相邻节点的关联而忽视了节点自身的特点导致的。 所以 Kipf 给出的解决方案是添加残差连接[2]，将节点自身特点从上一层直接传输到下一层：
在这个思路下，陆续有工作借鉴 DenseNet，将 residual 连接替换为 dense 连接，提出了自己的 module [3][4]：
其中， 表示拼接节点的特征向量。
最近，也有些工作认为直接将使用残差连接矫枉过正，残差模块完全忽略了相邻节点的权重，因而选择在 的基础上，对节点自身进行加强[5]：
在此基础上，作者进一步考虑了相邻节点的数量，提出了新的正则化方法：
另辟蹊径的模型宽度 —— multi-hops 等
随着图卷积渗透到各个领域，一些研究开始放弃深度上的拓展，选择效仿 Inception 的思路拓宽网络的宽度，通过不同尺度感受野的组合对提高模型对节点的表征能力。N-GCN[6]通过在不同尺度下进行卷积，再融合所有尺度的卷积结果得到节点的特征表示：
其中， ，
表示拼接节点的特征向量。原文中尝试了
和
等不同的归一化方法对当前节点
阶临域的进行信息汇聚，取得了还不错的效果。
也有一些工作认为 GCN 的各层的卷积结果是一个有序的序列：对于一个 层的 GCN，第
层捕获了
-hop 邻居节点的信息，其中
，相邻层
和
之间有依赖关系。因而，这类方法选择使用 RNN 对各层之间的长期依赖建模[7]：
即为：
随着图卷积的日益成熟，深层的图卷积已经在各个领域开花结果啦～ 相信在不久的将来，pruning 和 NAS 还会碰撞出新的火花，童鞋们加油呀！另外，有的同学私信想看我的论文中是怎样处理 over-smooth 的～可是由于写作技巧太差我的论文还没发粗去（最开始导师都看不懂我写的是啥，感谢一路走来没有放弃我的导师和师兄，现在已经勉强能看了），等以后有机会再分享叭～
参考
- ^Deeper insights into graph convolutional networks for semi-supervised learning https://arxiv.org/abs/1801.07606
- ^Semi-supervised classification with graph convolutional networks https://arxiv.org/abs/1609.02907
- ^Representation learning on graphs with jumping knowledge networks https://arxiv.org/abs/1806.03536
- ^Can GCNs Go as Deep as CNNs https://arxiv.org/abs/1904.03751
- ^Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks https://arxiv.org/abs/1905.07953
- ^N-GCN: Multi-scale graph convolution for semi-supervised node classification https://arxiv.org/abs/1802.08888
- ^Residual or Gate? Towards Deeper Graph Neural Networks for Inductive Graph Representation Learning https://arxiv.org/abs/1904.08035
1.请检查原始数据集中，节点特征是不是非常相似？
如果是：说明原始数据集存在该问题，不能认为结果都是GCN造成的
如果不是：请看下一条
2.减少网络的层数，看问题是否解决？
如果不是：如果模型本身的code或者数据处理存在问题，重新检查相应环节
如果是：首先要明确是否需要很深层的模型？需要的是解决问题，而不是炫技！
当然，到这里基本可以确定过度平滑就是由于深层GCN导致的了，原因在下面分析
为什么GCN会有过度平滑现象呢？
本质上而言，卷积（这里指深度学习中的概念）就是一种聚合预算（aggregate），当卷积核取特定值的时候，就是一种平滑运算。
CNN的平滑滤波
先不提GCN，从大家更熟悉的CNN谈起。当我们把一个3*3或者5*5的卷积核全部取为固定值为 或者
的时候，这是什么呢？这本质上就是图像里的平滑滤波！
更详细的内容可以参考我下面链接中的（2.2）节
哪位高手能解释一下卷积神经网络的卷积核？www.zhihu.com
那么CNN邻域里，为什么没人问这个问题呢？原因是卷积核都是parameter learning的，没人专门设置成上述的取值。
也许是拉普拉斯矩阵惹的祸
举个栗子，以下图1的graph结构为例：
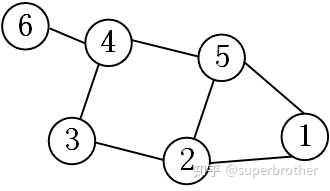图1 graph结构示意
如果进行一种这样的矩阵运算：
答案很明显，每个顶点的特征都会变成：
过度平滑的问题因此产生了。
现在我们想知道，深层GCN是不是产生了类似的问题？
以我的这个回答中第二种通用的GCN为例
superbrother：解读三种经典GCN中的Parameter Sharingzhuanlan.zhihu.com
即：
其中 是graph的邻接矩阵，
是为了实现self-accessible，
是
中每个顶点的度矩阵。运算
对
进行了归一化。
在之前的回答中，我提到过 是一个用于特征增强的线性变换，在这里不影响我们问题的本质，为了便于分析先将其去掉。
按照迭代递推，式（1）变为
现在目光自然就聚焦在 身上了。
为了清晰、直观地说明问题，这里下面以图1的结构为例，进行数值实验 。
从上面的实验我们发现：随着层数的增多（ 增大），
中低阶neighbor的系数逐渐减小，高阶neighbor的系数逐渐增大（从0开始增大）。收敛的结果是整个矩阵中元素的数值都非常接近。实际上当
，运算已经收敛，结果都是
的数值。
按照整体的逻辑思路，问题原因已经找到：是 的高次幂运算，产生了问题。CNN里可没有这样的家伙哦。
如何解决
上文的内容，已经分析了原因，归根结底是【卷积核】不行！
在不考虑换模型的情况下，有下面三种解决方案：
- Demystifying Graph Neural Network Via Graph Filter Assessment 这篇论文测评了不同核的效果，可以根据需求考虑一下。http://link.zhihu.com/target=https%3A//openreview.net/forum%3Fid%3Dr1erNxBtwr
- 直接解决高次幂运算的问题，当然可以通过修改卷积核正则化的方法。Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks
- 既然深层的卷积特征有问题，那把低层的结果保留下来，共同拼接成特征，问题也可以缓解。N-GCN: Multi-scale Graph Convolution for Semi-supervised Node Classification通过在不同邻居尺度下进行卷积，再融合所有尺度的卷积结果得到节点的特征表示。
10.12更新：我们组项目DeepGCNs在生物图数据PPI网络（实验发现加深56层/112层GCN就可以达到了F1 99.4，目前的SOTA）和点云数据PartNet上的附加实验已经开源https://github.com/lightaime/deep_gcns_torch 扩展版本的论文最近会挂到Arxiv上。欢迎关注。
———————-
泻药..首先要搞清楚图神经网络不能加深的原因是什么。常见的原因有三种：1）数据集太小，overfitting的问题，在一些数据上training acc为100%的大概率是这个问题，需要通过防止过拟合的技术来解决 2）vanishing gradient，这是CNN里一样存在的问题，当层数太深导致网络的参数不能得到有效的训练。这个问题可以加skip connections可以有效解决 3）over smoothing
写的很好，同一个连通分量里的节点会收敛的一个值，一个解决的方法是通过有效地改变图的结构或卷积的领接节点来解决。比如在点云里用动态knn/dilation来建边，但在其他图数据，这个方法会丢失边的信息。那还有什么方法能解决？目前我们已经有了一些很好的效果，具体我们后续论文会再深入研究。
其他同学@也提到了我们ICCV Oral的工作：DeepGCNs，这个工作主要是解决了vanishing gradient和over smoothing的问题，最开始是在点云上做的实验，正在做的TPAMI版本我们把14层的图网络MRConv用到了PPI数据，达到了F1 score 99.4的效果，是目前的start-of-the-art。PPI部分的实验代码近期会开源。
点云实验的代码、论文、slides都已开源。论文还有很多可以改善的地方，我们也还在做一些后续工作，欢迎交流：
Arxiv paper：
DeepGCNs: Can GCNs Go as Deep as CNNs?Github：
Tensorflow:
lightaime/deep_gcnsgithub.com
Pytorch:
lightaime/deep_gcns_torchgithub.com
都说GNN实际是个热传导，所以如果导热率太高，时间太长，最终就是温度达到单一温度。所以要降低导热率，或者缩短传导时间，才能形成有局部特征的分布模式。从消息传递的角度，就是要增加势能函数的差异性，或者说是降低系统温度，以及减少消息传递的循环次数。
对图网络只是略微了解 强答一下
图网络实际上做特征（结构）提取，对于图网络的结构进行表征，当网络层数过多的时候，类似于CNN中用两个 3*3 的卷积核可以获得 5*5 的感受野，当网络层数过多的时候，此时的表征实际上应该收敛到图的表示，也就是整个图全局的信息完全同步到每一个节点，而不是我们期待的结构信息（局部结构特征）。感觉最后的结果类似于Graph-Kernel出来的结果，将图embedding了而不是node-embedding。
如何解决？限制层数，能够表达一定程度的局部特征（结构）和全局特征（全局图信息）就好
以图卷积网络为例，截止于18年，我看到的情况还是最好支持两层结构；目前有一些基于CNN的思路做了些扩展的，据说可以支持更深的结构，比如类似于Resnet结构的图卷积，但是我记得这个文章是沙特的一个大学发表的，不知道效果究竟如何，里面是不是有一些隐藏条件。
关于图卷积网络，为何会出现平滑问题，这个问题本身在图卷积网络的初始论文《SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS 》这里面就有提到过，我个人怀疑这种over smoothing应当是同卷积设计的拉普拉斯方法有关；这里有一篇论文涉及到了这个问题《Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning》
卖一下自己的方法，简单好用，对oversmoothing很有效。并对oversmoothing以及DropEdge起效果的原因进行了理论分析。
DropEdge: Towards Deep Graph Convolutional Networks on Node Classification还有GitHub：
https://github.com/DropEdge/DropEdge
我看到有一些文章里用了门控机制来解决这个问题，比如这篇《Multi-hop Reading Comprehension across Multiple Documents by Reasoning over Heterogeneous Graphs》，可以参考
萝卜：《基于异构图推理的多文档多跳阅读理解》阅读笔记zhuanlan.zhihu.com
），还有《BAG: Bi-directional Attention Entity Graph Convolutional Network for Multi-hop Reasoning Question Answering》，参考
萝卜：BAG：面向多跳推理QA的双向注意力实体GCN网络zhuanlan.zhihu.com
针对GCN算子的无穷幂计算问题：
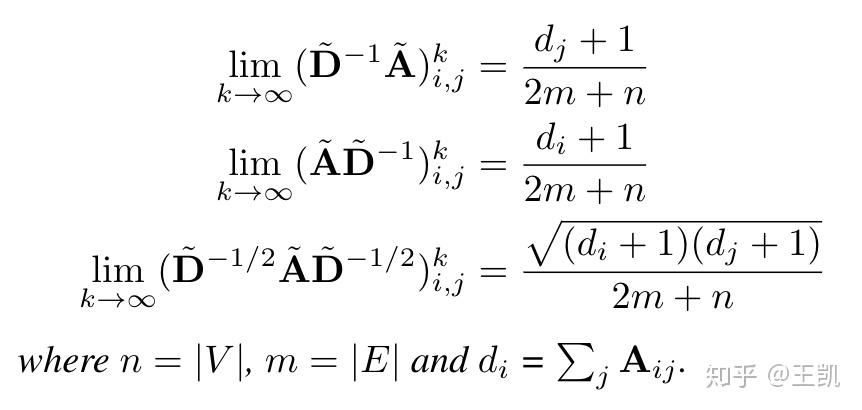+1是因为self-connected
附上numpy仿真代码：
import numpy as np
a=np.array([[1,1,1,1,1],[1,1,0,0,0],[1,0,1,0,0],[1,0,0,1,0],[1,0,0,0,1]])
d = np.diag(np.power(a.sum(1), -0.5))
dad = d.dot(a).dot(d)
dad.dot(dad).dot(dad).dot(dad).dot(dad).dot(dad).dot(dad).dot(dad).dot(dad).dot(dad).dot(dad).dot(dad)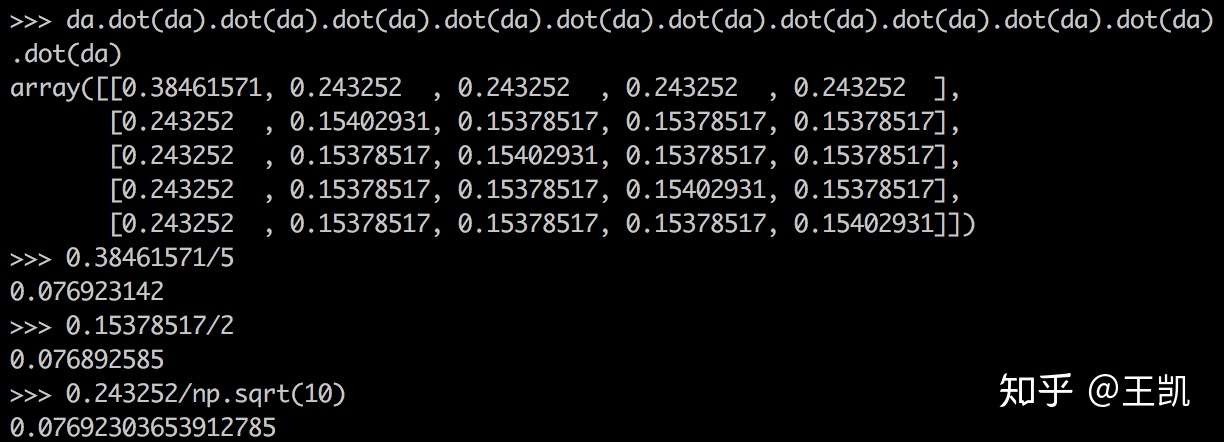
矩阵多次幂后的值的确和sqrt((d(i)+1)*(d(j)+1))成正比
GNN，或者更specific地说，GCN吧...最本质上是Laplacian Matrix特征向量线性基变换后的滤波。
修正后...
Laplacian operator其本身相当于是一个高通滤波器，再加上GCN原本的假设是多项式滤波/Chebyshev polynomial expansion，如果training出来的滤波系数是正，那么效果主要是平滑的...如果系数是负，那应该会让信号更加的bumpy...
（anyway...坐等更好的分析）