[总结]二进制状态压缩

---

目录

• 一、关于二进制状态压缩
  • 1.定义
  • 2.应用范围
• 二、二进制状态压缩的操作
• 三、具体应用
  • 例1：最短Hamilton路径
  • 例2：P2114 [NOI2014]起床困难综合症

一、关于二进制状态压缩

1.定义

二进制状态压缩，是指将一个长度为(m)的(bool)类型数组用一个二进制下有(m)位的整数表示并存储的方法。

2.应用范围

二进制状态压缩是状态压缩动态规划，宽度优先搜索状态压缩优化的重要基础。

二、二进制状态压缩的操作

我们在构建程序时一定要注意：

1. 在(m)位二进制数中，最低位为第0位，从右到左位数依次增加，最高位为(m-1)位。
2. 逻辑运算符，算术运算符存在优先级关系，如果不确定它们的优先级，建议增添( )来保证程序的正确性。
   运算符的优先级如下表所示：
   

二进制状态压缩的操作如下表所示：

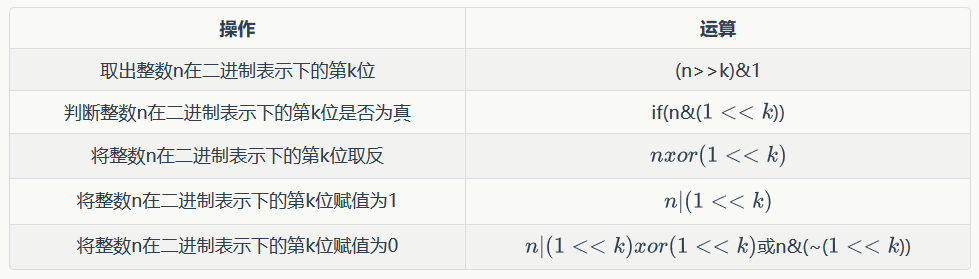
当(m)较大时,我们还可以使用C++STL中的(bitset)实现：(定义一个长度为1000的二进制串n)

[bitset<1000> n ]

三、具体应用

例1：最短Hamilton路径

1. 题目描述：
给定一张n个点的无向图，求起点0~（n-1）的最短Hamilton路径。
Hamilton路径的定义是恰好完全经过从起点0到终点(n-1)的所有点一次。
2.输入样例：

4
0 2 1 3
2 0 2 1
1 2 0 1
3 1 1 0

3. 分析：
我们要求最短Hamilton路径，因此我们需要枚举所有的Hamilton路径，即这n个点的全排列，并计算该路径的长度。这种做法的时间复杂度是(O(n imes n!))。
继续分析可以知道，我们需要记录哪些点已经走过，哪些点还没有走过。因为(nle 20)，所以我们可以采用状压Dp来描述这个状态。(f(sta，i))表示当前点为(i)，所有点走过状态(sta)时的最短路径长度。
转移方程的初始状态为(f(1,0)=0)，表示仅经过了起点0，结束状态为(f((1<<n)-1,n-1))。
转移方程为：(f(sta,i)=min(f(sta,i),f(sta~~xor~~(1<<i),k)+val(k,i)))。
因为(i)只会经过一次，所以当(i)走过时一定是上一次刚刚经过的。当然，(i)也可以经过(k)而到达的，我们枚举所有的(i)，(k)并取最小值。
4. 代码如下：

#include<bits/stdc++.h>
using namespace std;
int n,val[22][22],f[1<<22][22];
int main()
{
	scanf("%d",&n);
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			scanf("%d",&val[i][j]);
	memset(f,63,sizeof(f));
	f[1][0]=0;
	for(int sta=1;sta<=(1<<n)-1;sta++)
		for(int x=0;x<=n-1;x++){
			if(!(sta>>x)&1) continue;
			for(int y=0;y<=n-1;y++){
				if(!(sta>>y)&1) continue;
				f[sta][x]=min(f[sta][x],f[sta^(1<<x)][y]+val[y][x]);
			}
		}
	printf("%d",f[(1<<n)-1][n-1]);
	return 0;
}

例2：P2114 [NOI2014]起床困难综合症

1. 题目描述：
我们可以任选[0,m]的任意一个整数，现要找出在n次位运算后结果最大的一个整数。
2. 分析：
二进制下，位运算每一位的变化都是独立的。也就是说，最后结果的每一位只与对应选择的整数的对应位数有关。因此我们可以考虑按位处理，即每次选择第i位是1还是0，最后拼凑出最优的答案。在处理的时候要保证此时凑出的数在要求的范围内。
3. 代码如下：

#include<bits/stdc++.h>
using namespace std;
int n,m,ans;
pair<string,int> d[1000010];
inline int calc_val(int pos,int val){
	for(int i=1;i<=n;i++){
		int loc=(d[i].second>>pos)&1;
		if(d[i].first=="AND") val&=loc;
		else if(d[i].first=="OR") val|=loc;
		else if(d[i].first=="XOR") val^=loc;
	}
	return val;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1,t;i<=n;i++){
		char ch[20];
		scanf("%s%d",ch,&t);
		d[i]=make_pair(ch,t);
	}
	int ori=0,ans=0;
	for(int pos=30;pos>=0;pos--){
		int re0=calc_val(pos,0),re1=calc_val(pos,1);
		//re0为选择0后得到的答案，re1同理 
		if(ori+(1<<pos)<=m&&re1>re0) ans+=(re1<<pos),ori+=(1<<pos);
		//此时选1没有超出范围，且选1更优 
		else ans+=(re0<<pos);//选0更优 
	}
	printf("%d",ans);
	return 0;
}

---