1.1 逻辑回归原理详解
1.1.1 LR原理讲解+公式推导
从公式推导中详细讲解逻辑回归算法的原理。
线性回归模型:
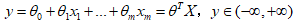
逻辑回归是用来估计一个实例属于某个特定类别的概率,是一个二分类算法,如果预估概率大于等于50%,则模型预测该实例为正类,反之,则预测为负类。
则需要把y从负无穷大到正无穷大映射为概率p从0到1,可以设置为:
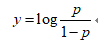
则:
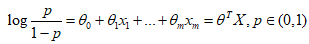
两边取e,整理后,得到逻辑函数:
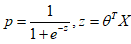
一旦逻辑回归模型估算出实例x属于正类的概率为p,那么就可以轻松推断出y值。
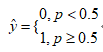
假设:
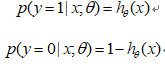
则:
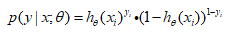
我们需要对系数θ估计,可以采用极大似然估计(MLE),通过最大化对数似然值来估计参数。
注:极大似然估计定义见下文详细讲解。
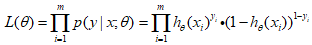
两边取对数,连乘会改为连加。
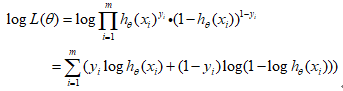
单个训练实例的成本函数:

当p接近于0时,-log(p)就会变得非常大,如果模型估计一个正类的概率接近于0,成本将会变得很高。同理,估计一个负类实例的概率接近于1,成本也会变得非常高。
整个训练集的成本函数即为训练实例的平均成本。逻辑回归成本函数表示如下。
逻辑回归成本函数(log损失函数):
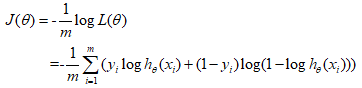
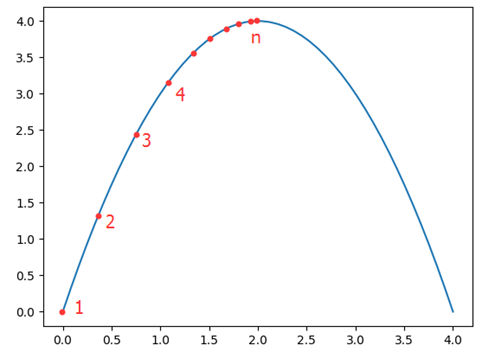
这是一个凸函数,通过梯度上升能够找出全局最大值。(只要学习率不是太高,又可以长时间等待)
对logL求某个系数θ的偏导:
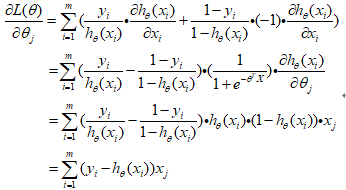
手写过程如下所示:

即:逻辑回归成本函数的偏导数为每个实例真实值与预测值的误差,将其乘以第j个特征值,并求和。
那么怎么获得系数呢?通过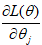 这个函数开口向下,使用梯度上升算法,获得全局最大值。
这个函数开口向下,使用梯度上升算法,获得全局最大值。
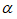 :学习率,自己给定,为固定值,可调整,不宜过高。
:学习率,自己给定,为固定值,可调整,不宜过高。
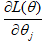 :对求偏导
:对求偏导
θ:初始化一个任意值
θ初始化一个值后,可以计算得到预测的y值,计算预测误差,得到偏导,通过梯度上升算法更新θ值。
我们反过来回顾下:
通过梯度上升算法获得拟合效果最好的系数θ,根据sigmoid函数,输入特征X代入,得到概率p值,通过P值是否大于0.5,最终得到预测结果y。
1.1.2 逻辑回归的应用场景和优缺点
1.1.2.1 应用场景
- Logistic回归是一种用于解决二分类问题的机器学习方法,是一种判别模型:表现为直接对条件概率P(y|x)建模,而不关心背后的数据分布P(x,y)
- 用于估计某种事物的可能性。比如某用户购买某商品的可能性、某病人患有某种疾病的可能性、以及某广告被用户点击的可能性等。
1.1.3 优缺点
1.1.3.1 优点
- 系数表示该特征的权重大小,可解释性强,原理基于线性回归,易于理解。
- 计算代价不高
1.1.3.2 缺点
- 容易欠拟合,分类精度可能不高
1.1.4 专业名词介绍
1.1.4.1 极大似然估计
极大似然估计,又称最大似然估计。
极大似然估计的原理,用一张图片来说明,如下图所示:
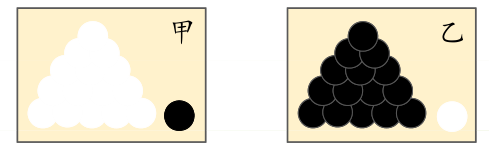
试验是取出一个球是黑球,第一印象就是这个黑球最像是从乙箱取出来的,这个推断符合人们的经验事实。“最像”就是“最大似然”之意,就是概率性是最大的。
总而言之,极大似然估计的目的就是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
原理:极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。以下仅介绍总体X为离散型的情况。
若总体X(即输入特征)属离散型,其分布律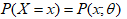 已知(即输出结果y已知), θ为待估参数,设
已知(即输出结果y已知), θ为待估参数,设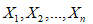 为来自X的样本,则
为来自X的样本,则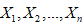 的联合分布律为
的联合分布律为
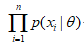
又设 是相应于样本
是相应于样本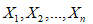 的一个样本值,即事件
的一个样本值,即事件 发生的概率为:
发生的概率为:
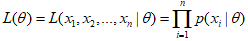
如果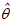 是参数空间中能使似然函数
是参数空间中能使似然函数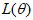 最大的θ值,则应该是“最可能”的参数值,那么就是θ的极大似然估计量。它是样本集的函数,记作:
最大的θ值,则应该是“最可能”的参数值,那么就是θ的极大似然估计量。它是样本集的函数,记作:

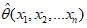 称作极大似然函数估计值。
称作极大似然函数估计值。
1.1.4.2 凸函数、凹函数
1.1.4.2.1 函数凹凸性定义
以下为国内的凹凸性定义,与国外凹凸性定义相反。
设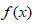 在区间I上有定义
在区间I上有定义
(1) 若对任意的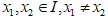 ,有
,有

则称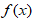 在
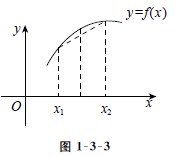
在 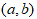 内为凸函数,如图1-3-3所示。
内为凸函数,如图1-3-3所示。
(2) 若对任意的 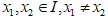 ,有
,有

则称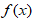 在
在 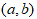 内为凹函数,如图1-3-4所示。
内为凹函数,如图1-3-4所示。
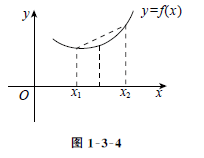
1.1.4.2.2 函数凹凸判别法
定理:
(1) 若在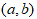 内有
内有 ,则
,则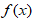 在
在 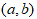 内为凸函数
内为凸函数
(2) 若在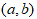 内有
内有 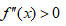 ,则
,则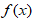 在
在 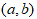 内为凹函数
内为凹函数
1.1.4.2.3 逻辑回归目标函数是凸函数证明
目标函数:

一阶偏导:
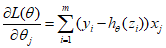
证明过程见LR公式推导部分。
二阶偏导:
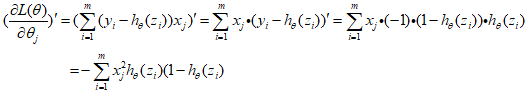
由于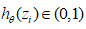 ,即
,即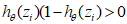 ,则
,则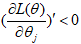 恒成立,所以目标函数是凸函数。
恒成立,所以目标函数是凸函数。