最短路径
问题背景:地图上有很多个城市,已知各城市之间距离(或者是所需时间,后面都用距离了),一般问题无外乎就是以下几个:
- 从某城市到其余所有城市的最短距离【单源最短路径】
- 所有城市之间相互的最短距离【任意两点最短路径】
- 各城市距离一致,给出需要最少中转方案 【最少中转】
深度优先搜索
适用范围:啥都不适用,只能处理n<10的情况
深搜求最短路径的思想和用深搜迷宫寻路有一点像,找出所有的从起点到目标点的路径,选出其中最短的一条。
此算法仅供娱乐参考,实际不会用它的,因为算法复杂度是$O(n!)$
深度优先搜索:
const int inf = 1 << 30; int M[50][50]; bool fuck[50]; int n, res; //cur-当前所在城市编号,dis-当前已走过的路径 void dfs(int cur, int dis) { //若当前的路径值已比之前找到的最短路大,没必要继续往下搜索了,其实没什么必要,深搜本来就属于暴力算法,这个小优化属于杯水车薪 if (dis > res) return; //当前已到达目的城市,更新min if (cur == n) { res = min(res, dis); return; } //对1~n号城市依次尝试 for (int i = 1; i <= n; i++) { //若cur与i之间有路,且i没有在已走过的路径中 if (M[cur][i] != inf && !fuck[i]) { fuck[i] = true; //标记i为已走的路径 dfs(i, dis + M[cur][i]); //继续搜索 fuck[i] = false; //回溯 } } }

#include <iostream> #include <algorithm> #include <fstream> #include <cstdio> #include <queue> using namespace std; const int inf = 1 << 30; int M[50][50]; int path[50]; bool fuck[1000]; int n, m, res = inf, cnt; //cur-当前所在城市编号,dis-当前已走过的路径 void dfs(int cur, int dis,int destination,int k) { //若当前的路径值已比之前找到的最短路大,没必要继续往下搜索了,其实没什么必要,深搜本来就属于暴力算法,这个小优化属于杯水车薪 //if (dis > res) // return; //当前已到达目的城市,更新min if (cur == destination) { res = min(res, dis); //cnt++; for (int i = 0; i < k; i++) { cout << path[i] << ' '; } cout << endl; return; } //对1~n号城市依次尝试 for (int i = 1; i <= n; i++) { //若cur与i之间有路,且i没有在已走过的路径中 if (M[cur][i] != 0 && M[cur][i] != inf && !fuck[i]) { fuck[i] = true; //标记i为已走的路径 path[k] = i; dfs(i, dis + M[cur][i], destination, k + 1); //继续搜索 fuck[i] = false; //回溯 } } } int main() { #ifdef LOCAL fstream cin("data.in"); #endif // LOCAL cin >> n >> m; for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { if (i != j) M[i][j] = inf; } } for (int i = 0; i < m; i++) { int c1, c2, c3; cin >> c1 >> c2 >> c3; M[c1][c2] = c3; M[c2][c1] = c3; } cnt = 0; res = inf; fuck[1] = true; path[0] = 1; dfs(1, 0, 4, 1); return 0; }
宽度优先搜索
适用范围:最少中转方案,处理n的级别看脸
假如现在是最少中转方案问题(或者所有边的权值一致) ,问从城市1到城市4需要经过的最少中转城市个数。
这类问题和宽搜求迷宫的最短路径思想完全一样,从开始点逐层扩展,找到目标停止。
宽搜的算法复杂度也是$O(n!)$,不过看脸,如果在前面几层就找到目标了,就比较快。
也就是目标点需要中转几次,如果一次都不要中转,那么第二层就能搜索到;如果需要中转n-2次,那就得搜索到最后一层,就也是$O(n!)$了
宽度优先搜索:
int M[50][50]; int path[50]; bool fuck[1000]; int n, m, res = inf, cnt; int bfs(int start, int destination){ queue<pair<int, int>> q; //城市编号、当前是第几座城市 q.push({ start,0 }); //把起始点加入队列 fuck[start] = true; //标记为已在路径中 while (!q.empty()){ int cur = q.front().first, dis = q.front().second; q.pop(); for (int i = 1; i <= n; i++) { //如果当前点到i点有路,并且当前还没有加入队列中 if (M[cur][i] != inf && !fuck[i]) { q.push({ i,dis + 1 }); fuck[i] = true; if (i == destination) //如果发现了目标点 return dis;//这里具体是算多少步看题目咋问了 } } } }

#include <iostream> #include <algorithm> #include <fstream> #include <cstdio> #include <queue> using namespace std; const int inf = 1 << 30; int M[50][50]; int path[50]; bool fuck[1000]; int n, m, res = inf, cnt; int bfs(int start, int destination){ queue<pair<int, int>> q; //城市编号、当前是第几座城市 q.push({ start,0 }); //把起始点加入队列 fuck[start] = true; //标记为已在路径中 while (!q.empty()){ int cur = q.front().first, dis = q.front().second; q.pop(); for (int i = 1; i <= n; i++) { //如果当前点到i点有路,并且当前还没有加入队列中 if (M[cur][i] != inf&& !fuck[i]) { q.push({ i,dis + 1 }); fuck[i] = true; if (i == destination) //如果发现了目标点 return dis;//这里具体是算多少步看题目咋问了 } } } } int main() { #ifdef LOCAL fstream cin("data.in"); #endif // LOCAL cin >> n >> m; for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { if (i != j) M[i][j] = inf; } } for (int i = 0; i < m; i++) { int c1, c2, c3; cin >> c1 >> c2 >> c3; M[c1][c2] = c3; M[c2][c1] = c3; } cout << bfs(1, 4); return 0; }
这两个算法我觉得算是迷宫寻路算法的延伸,可以看下迷宫寻路问题全解,用在求最短路径中的话,效率太低,无法解决实际问题。
接下来才是重点。
迪杰斯特拉(Dijkstra)算法
适用范围:不含负权边的单源最短路径、最少中转
不含负权边就是所有路径长度大于0,牵扯到负权边,请参考 Bellman-Ford算法
思路图解
维护一个$dis$数组记录起点(按题目要求来,这里取$1$) 到达的所有节点的距离。(规定到自己的路径长度0,到不了的点是 inf(极大值))
找出当前距离$1$最近的结点:$4$。(已经访问过的,我们标记为红色,不再次访问)
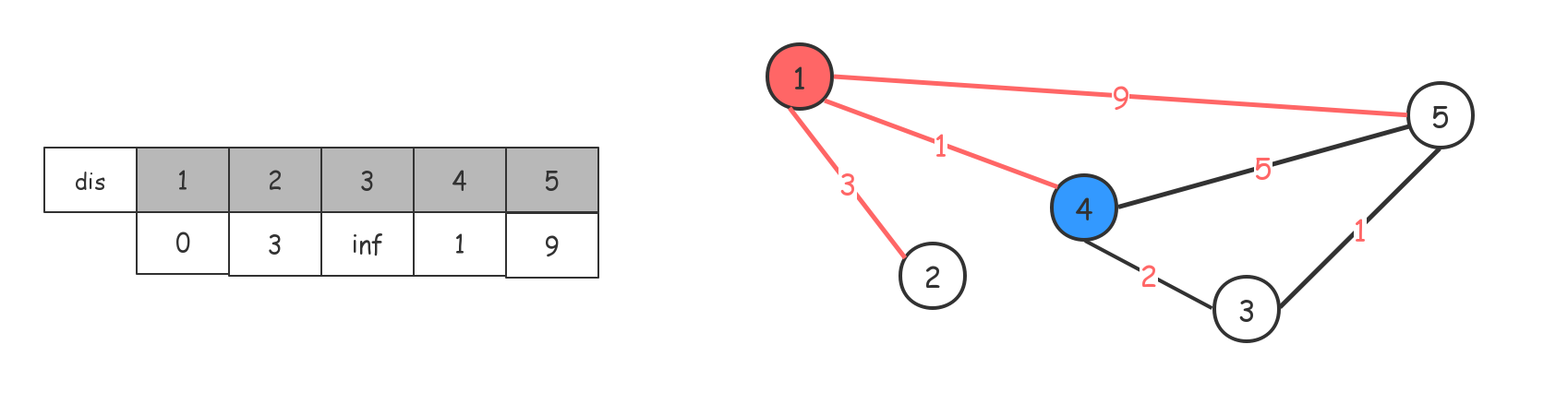
借助$4$节点,对$dis$数组进行更新(就是如果结点$1$借助结点$4$到别的结点有更短的路径,就对$dis$数组进行值替换)
找出当前距离$1$最近的结点:$2$。
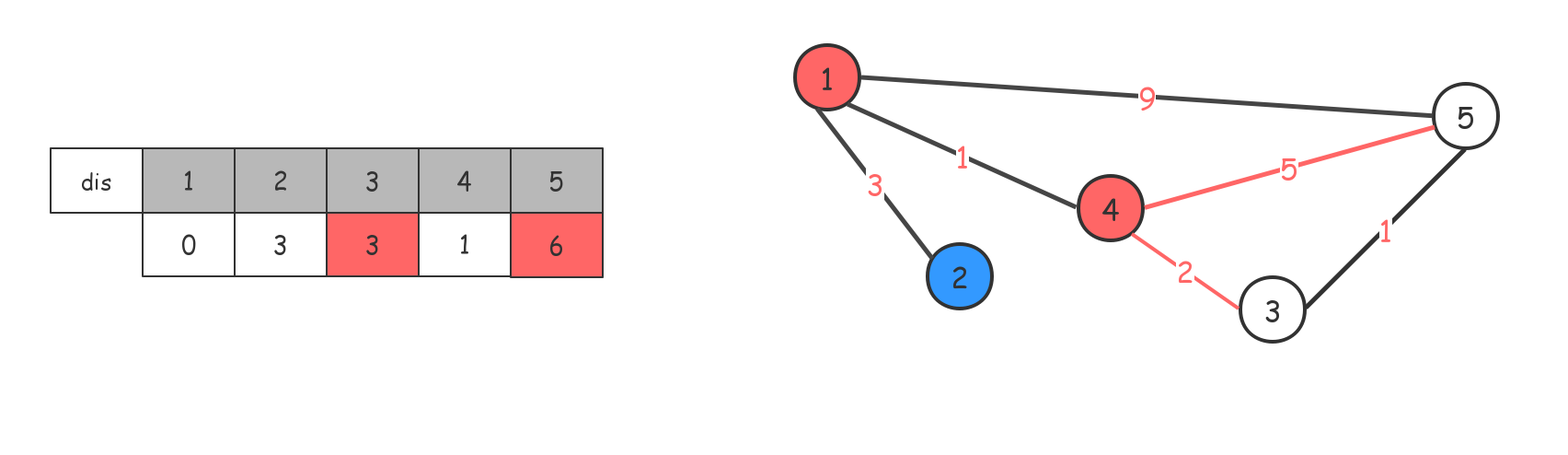
走到$2$,无法更新$dis$数组,无操作。
找出当前距离$1$最近的结点:$3$。
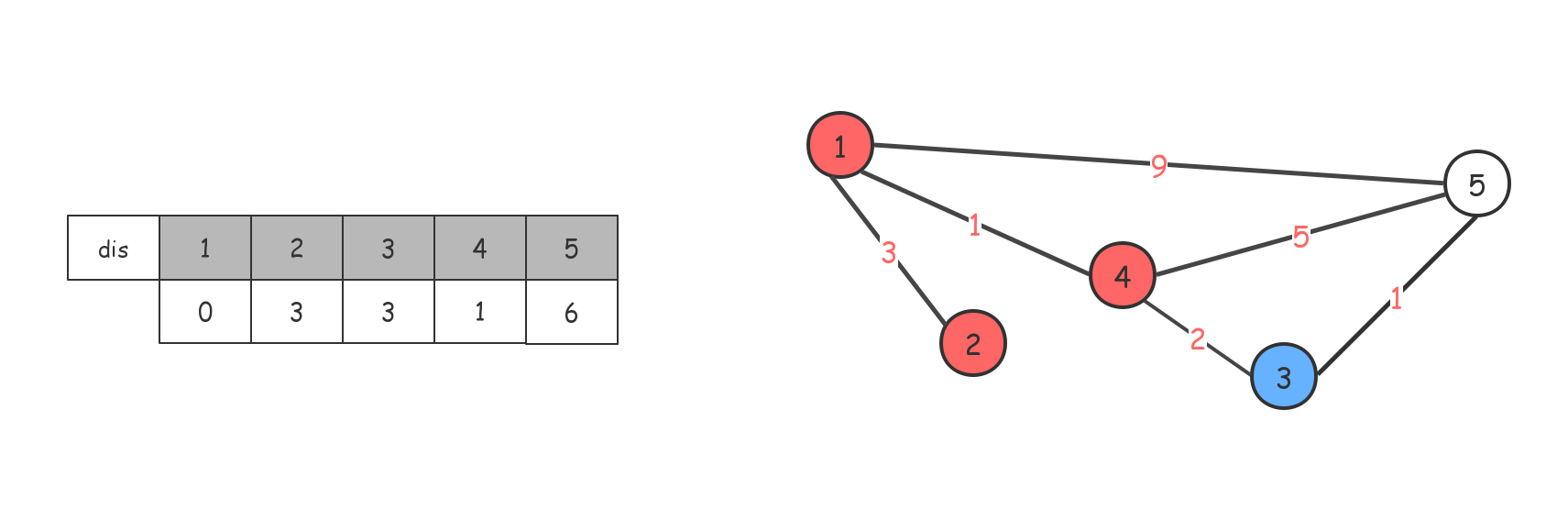
借助$3$节点,对$dis$数组进行更新,最后走到$5$节点,退出。(实际过程中,走到最后一个节点,别的节点都访问过,进行标记了,什么也不会做)。
这个时候$dis$数组就是从起点$1$到所有节点的最短路径了,如果还有$inf$表示不是连通图。
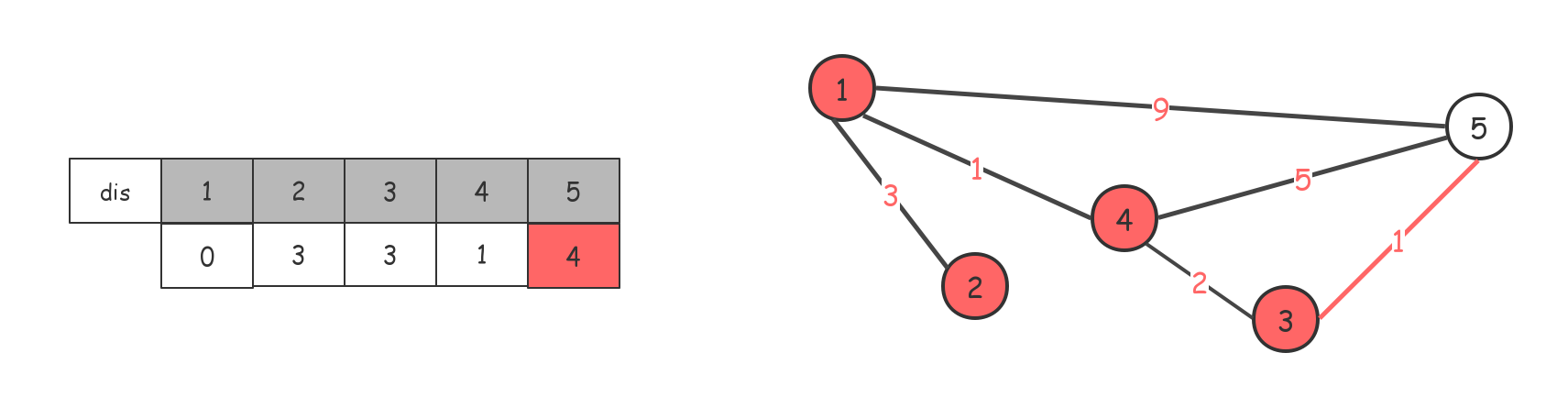
简单版(邻接矩阵+优先级队列):
测试题目:http://acm.hdu.edu.cn/showproblem.php?pid=2544 (数据很弱,建议再做后面一题)

#include <fstream> #include <iostream> #include <queue> #include <algorithm> #include <string.h> using namespace std; const int inf = 1 << 30; int n, m; bool book[1001]; int M[1001][1001]; int dis[1001]; class P { public: int to, dis; P(int t, int d) :to(t), dis(d) {} bool operator< (P a) const { return a.dis < dis; } }; priority_queue<P>q; void initialize() { fill(book, book + n + 1, false); fill(dis, dis + n + 1, inf); for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { if (i != j)M[i][j] = inf; } } } void dijkstra() { dis[1] = 0; q.push({ 1, 0 }); while (!q.empty()) { int v = q.top().to; q.pop(); if (book[v])continue; book[v] = true; for (int i = 1; i <= n; i++) { if (!book[i] && dis[i] > dis[v] + M[v][i]) { dis[i] = dis[v] + M[v][i]; q.push({ i, dis[i] }); } } } } int main() { #ifdef LOCAL fstream cin("data.in"); #endif // LOCAL while (cin >> n >> m) { if (n == 0 && m == 0)break; initialize(); for (int i = 0; i < m; i++) { int A, B, C; cin >> A >> B >> C; M[A][B] = C; M[B][A] = C; } dijkstra(); cout << dis[n] << endl; } return 0; }
正式版(邻接表+优先级队列)
测试题目:https://www.luogu.org/problemnew/show/P4779

#include <fstream> #include <iostream> #include <stdio.h> #include <queue> using namespace std; int dis[100001]; bool fuck[100001]; const int inf = 1 << 30; int n, m, s; struct ENode { int to, dis; ENode* next = NULL; ENode() {} ENode(int t, int d) :to(t), dis(d) {} void push(int t, int d) { ENode* p = new ENode(t, d); p->next = next; next = p; } bool operator<(ENode e)const { return e.dis < dis; } }head[100005]; void dijkstra() { priority_queue<ENode>q; fill(dis, dis + n + 1, inf); dis[s] = 0; q.push(ENode(s, 0)); while (!q.empty()) { //获得当期距离 源点 最近的点 int v = q.top().to, d = q.top().dis; q.pop(); if (fuck[v])continue; fuck[v] = true; ENode* p = head[v].next; while (p) { int to = p->to; if (!fuck[to] && dis[to] > d + p->dis) { dis[to] = d + p->dis; q.push(ENode(to, dis[to])); } p = p->next; } } } int main() { #ifdef LOCAL fstream cin("data.in"); #endif // LOCAL int c1, c2, c3; cin >> n >> m >> s; for (int i = 0; i < m; i++) { //cin >> c1 >> c2 >> c3; scanf("%d%d%d", &c1, &c2, &c3); head[c1].push(c2, c3); } dijkstra(); for (int i = 1; i <= n; i++) { printf("%d ", dis[i]); } cout << endl; return 0; }
提一句如果是要求找最少中转方案,那么就把每个边的权值都设为1,在求最短路径即可。
时间复杂度分析
一般默认迪杰斯特拉算法复杂度为$O(n^2)$,也就是每次从$dis$中获取路径最短的结点,需要花费线性的时间$O(n)$,但这是普通情况下。【$n$为顶点数】使用优先级队列后,从$dis$中获取路径最短的结点只需要$O(logn)$(因为我们用了一个标记数组,所以堆中的数据个数不可能会超过$n$,所以是$O(logn)$,如果没有加这个复杂度是$O(logm)$,m为边的个数)。所以,堆优化的迪杰斯特拉算法时间复杂度为$O((m+n)logn)$。
关于负权边
$Dijkstra$是一种基于贪心策略的算法。每次新扩展一个路径最短的点,更新与它相邻的所有点。当所有边权为正时,由于不会存在一个路程更短的没扩展过的点,所以这个点的路程就确定下来了,这保证了算法的正确性。但也正因为这样,这个算法不能处理负权边,因为扩展到负权边的时候,某个点会产生更短的路径,但可能该点已被标记。
比如这张图,按照Dijkstra算法,假如起点是A,一定会先找到C,并且认为已经找到A到C最短路径,在没有负边的时候是这样的,但现在B到C是-2,这就出现错误了。

Floyd算法
Floyd算法属于动态规划,实现容易,好理解,但缺点就是时间复杂度高是$O(n^3)$。
$M [ j ] [ k ]$ 表示从$ j$ 到 $k$ 的路径,而 $i$ 表示当前 $j$ 到 $k$ 可以借助的点;红色部分表示,如果 $j$ 到 $i$ ,$i$ 到 $k$ 是通的,就将 $j$ 到 $k$ 的值更新为$min(M[j][i] + M[i][k],M[j][k] )$
for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { for (int k = 1; k <= n; k++) { if (j != k && M[j][i] != inf && M[i][k] != inf) M[j][k] = min(M[j][i] + M[i][k], M[j][k]); } } }
给个题目链接,可以交试一下:http://www.dotcpp.com/oj/problem1709.html

#include <iostream> #include <queue> using namespace std; #define inf 2147483647 int M[1000][1000]; int main() { int n; queue<int>q; cin >> n; for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { cin >> M[i][j]; if (M[i][j] == 0 && i != j)M[i][j] = inf; } } for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { for (int k = 1; k <= n; k++) { if (M[j][k] != 0) { if (M[j][i] != inf && M[i][k] != inf) { M[j][k] = M[j][i] + M[i][k] < M[j][k] ? M[j][i] + M[i][k] : M[j][k]; } } } } } for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { if (M[i][j] == inf)cout << -1 << " "; else cout << M[i][j] << " "; } cout << endl; } return 0; }
Dijkstra & Floyd 对比
$Dijkstra$算法的复杂度为$O(n^2)$【不考虑堆优化的情况】,如果采用Dijkstra算法来计算图中任两点之间的最短距离,复杂度也为$O(n^3)$,虽然复杂度相同,但是看代码,两个算法运算量差了很多,也就是$Dijkstra$算法输在了常数项。但是堆优化后的$Dijkstra$算法,还是要完全优于$Floyd$算法的。
对比: