这尼玛是贪心。。。QAQ
有两种思路：
一种是把奶牛按可接受spf上限排序，把防晒霜按spf值升序排序。然后每头牛从可选的防晒霜中选spf值最小的。
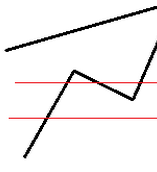（如图，红线表示防晒霜的spf值，上下两黑线表示奶牛可接受的spf值上限和下限）
显然选spf值最小的防晒霜对之后的奶牛影响最小。。
枚举每头奶牛，在剩下的防晒霜里再枚举一次。。。复杂度O(C*L)，（当然也可以用权值线段树之类的来优化，只是没第二种方便
另一种思路是把奶牛按可接受spf下限排序，防晒霜也是按spf值升序排序。对于每种防晒霜，选能接受它的牛里面spf上限最小的（当然了可能能选多头牛）。
（图的意思同上）
能接受当前防晒霜的奶牛中，可接受spf值上限越小的以后分配到防晒霜的可能就越小。。所以越应该给它。。。
维护一个小根堆，枚举防晒霜时，先把能接受的奶牛（的可接受spf上限值）加进堆里，再把堆顶那些不合法的奶牛去掉（上限值比当前防晒霜spf值还小的）。。最后从堆里出掉cover头奶牛就行了。。时间复杂度O(ClogC)
然而我只写了第一种(逃
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int maxn=2523; 7 struct zs{ 8 short l,r; 9 }a[maxn]; 10 struct zs1{ 11 short spf,num; 12 }b[maxn]; 13 short i,j,k,n,m,ans; 14 bool u[maxn]; 15 short ra;char rx; 16 inline short read(){ 17 rx=getchar();ra=0; 18 while(rx<'0'||rx>'9')rx=getchar(); 19 while(rx>='0'&&rx<='9')ra*=10,ra+=rx-48,rx=getchar();return ra; 20 } 21 bool cmp(zs a,zs b){ 22 return a.r<b.r; 23 } 24 bool cmp1(zs1 a,zs1 b){ 25 return a.spf<b.spf; 26 } 27 int main(){ 28 n=read();m=read(); 29 for(i=1;i<=n;i++)a[i].l=read(),a[i].r=read(); 30 sort(a+1,a+1+n,cmp); 31 for(i=1;i<=m;i++)b[i].spf=read(),b[i].num=read(); 32 sort(b+1,b+1+m,cmp1); 33 for(i=1;i<=m&&ans<n;i++){ 34 short tmp=0; 35 for(j=1;j<=n&&tmp<b[i].num&&ans<n;j++) 36 if(!u[j]&&a[j].l<=b[i].spf&&a[j].r>=b[i].spf)u[j]=1,tmp++,ans++; 37 } 38 printf("%d ",ans); 39 return 0; 40 }