马拉车算法总结

【算法简述】

马拉车（Manacher）算法是在O（n）时间内解决寻找源字符串的最长回文子串S的问题的算法。

朴素算法情况下对于每一个S[i]都要左右遍历其最大回文子串，所以时间复杂度是O（n²）

【算法原理】

充分利用之前求得的S【j】，为求S【i】服务。

预处理：在每个字符左右两边插入#将字符串变成奇数串

算法核心：

p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;

其中p[i]为S[i]的回文半径，mx为i之前某一回文串右侧最远延伸到的位置，id为该回文串的中心点位置，很显然从mx的对称点到mx这一段是关于id对称的。

如何利用之前求得的s[j]来求s[i]的回文串长度呢？
分情况讨论
(1) 当 i在mx左侧，p[j] < mx - i,即S[j]的回文子串的左端点不会超过mx的对称点，那么很显然S[i]的回文子串的右端点不会超过mx，所以此时取P[i] = p[j]

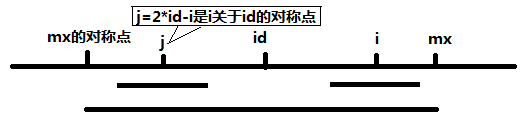
（2）当i在mx左侧， p[j] > mx - i时，即S[j]的回文子串的左端点超过mx的对称点，那么很显然S[i]的回文子串的右端点至少要到mx，至于mx右侧的，只能一个一个匹配以确定p[i]了。

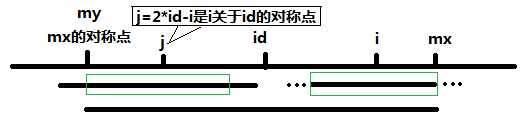
（3）当i在mx右侧，即i > mx,初始化p[i] = 1.这时候很显然，mx和id是要更新的。因为此时回文串右侧延伸的位置已经超过mx了。

【模板】

 为了最后返回字符串的参数传入方便，在字符串加了#的基础上又加了$

//返回源字符串S的最长回文子串 
string Manacher(string s){
    //预处理源串 
    string t = "$#";
    for(int i=0; i<s.size(); i++){
        t+=s[i];
        t+="#";
    }
    //新建p数组,大小和t串一致，初始化为0 ，p[i]表示以t[i]为中心的回文串半径 
    vector<int> p(t.size() , 0); 
    
    //设定重要参数 mx(某回文串延伸到的最右边下标),id(mx所属回文串中心下标),
    //reCenter（结果最大回文串中心下标）,reLen（最大长回文长度） 
    int mx = 0, id = 0, reCenter = 0, reLen = 0;
    
    //遍历t字符串
    for(int i=1; i<t.size(); i++){
        //核心算法 
        p[i] = mx > i ? min(mx - i , p[2*id - i]) : 1;
        
        //上面的语句只能确定i~mx的回文情况，至于mx之后的部分是否对称，就只能老老实实去匹配了，匹配一个p[i]++ 
        while(t[i + p[i]] == t[i - p[i]]) p[i]++;
        
        //当t[i]匹配的 右边界超过mx时mx和id就更新 
        if(i+p[i] > mx){
            mx = i+p[i];
            id = i;
        }
        //更新结果数据 
        if(p[i] > reLen){
            reLen = p[i];
            reCenter = i;    
        }
    }
    
    return s.substr((reCenter - reLen) / 2 , reLen - 1)  ;
    
}