Eat the Trees
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2303 Accepted Submission(s): 1124
Problem Description
Most of us know that in the game called DotA(Defense of the Ancient), Pudge is a strong hero in the first period of the game. When the game goes to end however, Pudge is not a strong hero any more.
So Pudge’s teammates give him a new assignment—Eat the Trees!
The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.
Now Pudge has a question, how many ways are there to eat the trees?
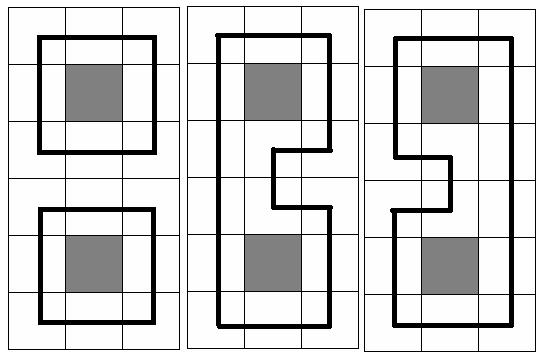
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))
So Pudge’s teammates give him a new assignment—Eat the Trees!
The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.
Now Pudge has a question, how many ways are there to eat the trees?
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))

Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.
Output
For each case, you should print the desired number of ways in one line. It is guaranteed, that it does not exceed 263 – 1. Use the format in the sample.
Sample Input
2
6 3
1 1 1
1 0 1
1 1 1
1 1 1
1 0 1
1 1 1
2 4
1 1 1 1
1 1 1 1
Sample Output
Case 1: There are 3 ways to eat the trees.
Case 2: There are 2 ways to eat the trees.
这篇文章写的不错https://wenku.baidu.com/view/e5314c16bcd126fff7050bf7.html
具体思路里面都有,代码里用x表示第i行第j列的下插头,y表示右插头,转移。
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; int t,n,m,dp[18][18][1<<13]; int Map[105][105]; int main() { scanf("%d",&t); while(t--) { memset(dp,0,sizeof(dp)); scanf("%d %d",&n,&m); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { scanf("%d",&Map[i][j]); } dp[0][m][0]=1; for(int i=1;i<=n;i++) { for(int k=0;k<(1<<m);k++) dp[i][0][k<<1]=dp[i-1][m][k]; for(int j=1;j<=m;j++) for(int sta=0;sta<(1<<(m+1));sta++) { int y=1<<j; int x=1<<(j-1); if(Map[i][j]) { if((sta&x)!=0&&(sta&y)!=0) { dp[i][j][sta]=dp[i][j-1][sta-x-y]; }else if((sta&x)==0&&(sta&y)==-0) { dp[i][j][sta]=dp[i][j-1][sta+x+y]; }else dp[i][j][sta]=dp[i][j-1][sta^x^y]+dp[i][j-1][sta]; }else { if((sta&x)==0&&(sta&y)==0) { dp[i][j][sta]=dp[i][j-1][sta]; }else dp[i][j][sta]=0; } } } cout<<dp[n][m][0]<<endl; } }
总的来说就是考虑把第i行,第j列的格子的右下插头的方案数从第i行第j列的左上插头中转移过来。