前面我们讲了 QR 分解有一些优良的特性,但是 QR 分解仅仅是对矩阵的行进行操作(左乘一个酉矩阵),可以得到列空间。这一小节的 SVD 分解则是将行与列同等看待,既左乘酉矩阵,又右乘酉矩阵,可以得出更有意思的信息。奇异值分解( SVD, Singular Value Decomposition ) 在计算矩阵的伪逆( pseudoinverse ),最小二乘法最优解,矩阵近似,确定矩阵的列向量空间,秩以及线性系统的解集空间都有应用。
1. SVD 的形式
对于一个任意的 m×n 的矩阵 A,SVD 将一个矩阵分解为三个特殊矩阵的乘积, 国外还做了一个视频——SVD 之歌:
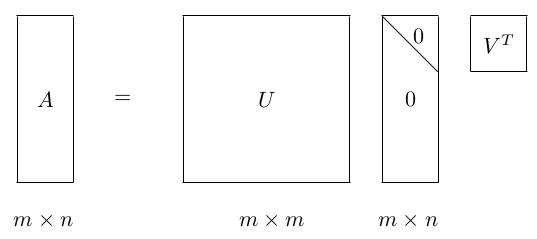
其中, U 和 是酉矩阵,
是对角线矩阵。注意酉矩阵只是坐标的转换,数据本身分布的形状并没有改变,而对角矩阵,则是对数据进行了拉伸或者压缩。由于 m
>= n,又可以写成下面这种 thin SVD 形式:
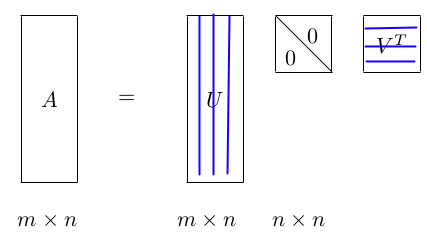
2. SVD 的几何解释
考虑 A 是 2×2 的简单情况。我们知道,一个几何形状左乘一个矩阵 A 实际上就是将该形状进行旋转、对称、拉伸变换等错切变换, A 就是所谓的 shear 矩阵。比如可以将一个圆通过左乘 A 得到一个旋转后的椭圆。
举个例子,假设 A 对平面上的一个圆进行变换:
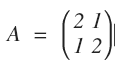
如果只看矩阵 A, 我们几乎无法直观看到圆是如何变换的。变换前的圆是:
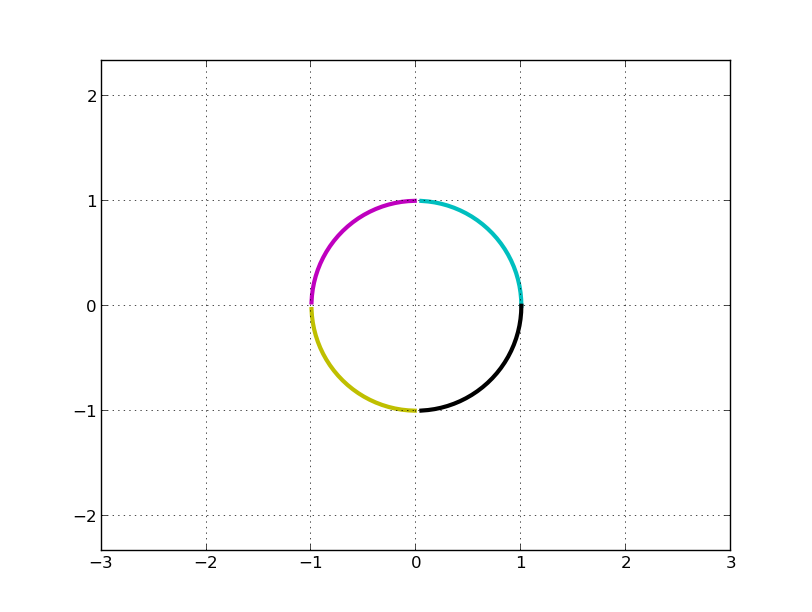
C, M, Y, K 分别表示第一、二、三、四象限。左乘 A 矩阵后得到:
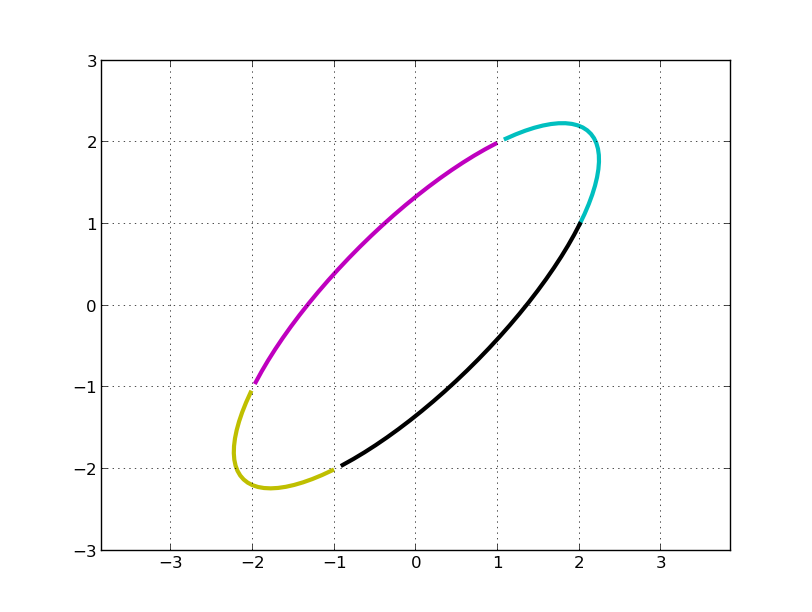
我们的问题是,旋转了多少度?伸缩的方向是多少?最大伸缩比例是多少?
利用这个在线工具对 A 进行 SVD 分解:
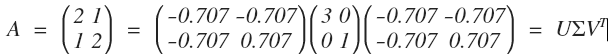
明显,我们看到 A 变换实际上是先对圆顺时针旋转 45°(可以看做是坐标轴逆时针宣战了 45°,主成分方向),再关于 x 轴对称(第一行乘以 -1), 即左乘 V^T:
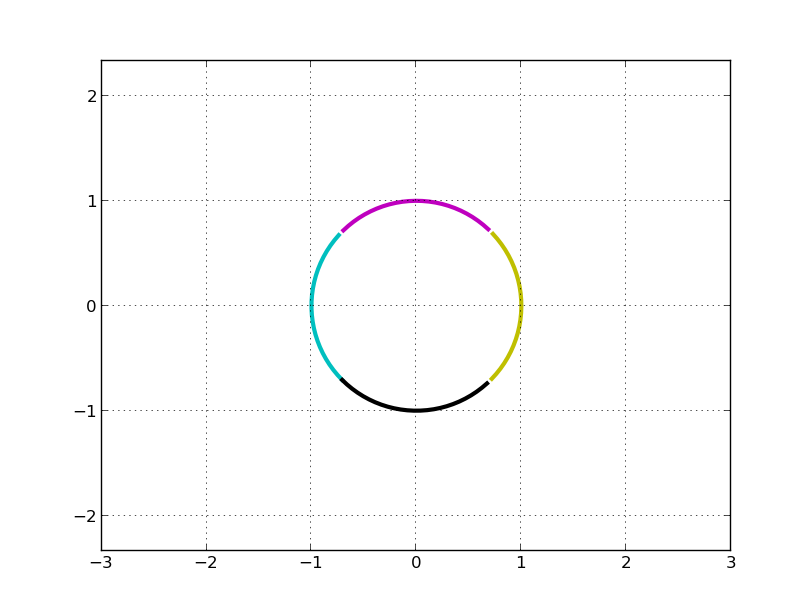
然后在 x 方向拉伸 3 倍(左乘S):
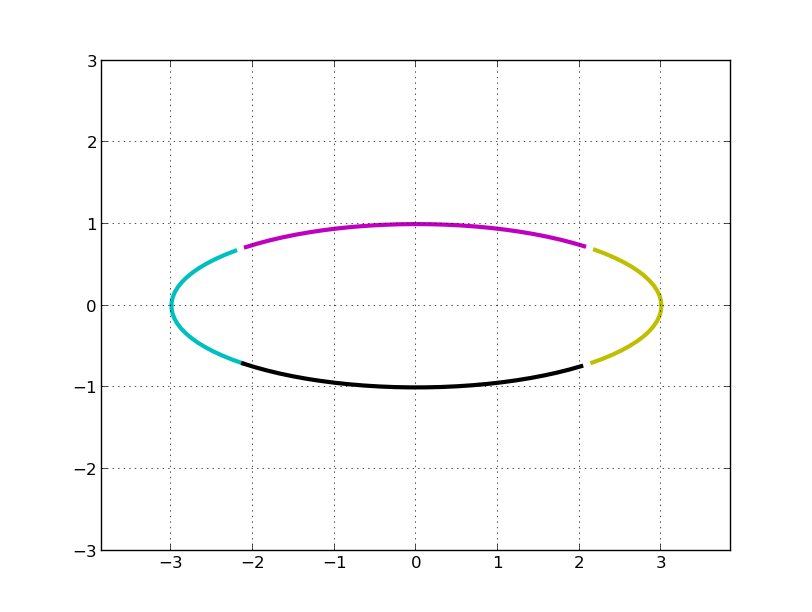
最后再顺时针旋转 45°,再关于 x 轴对称(第一行乘以 -1, 两次对称操作抵消了), 即左乘 U:
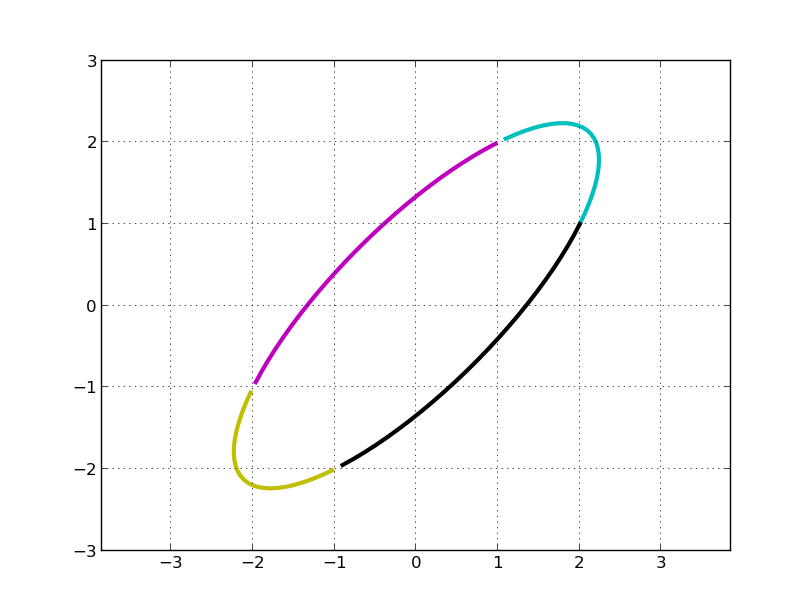
上述绘图过程的 python 代码如下:
1 # -*- coding=utf-8 2 #!/usr/bin/python2.7 3 4 from pylab import * 5 6 7 def plotCircle(before, M=matrix([[1, 0], [0, 1]])): 8 '''before: 变换前的矩阵 9 M: 变换矩阵,默认为单位矩阵 10 返回变换之后的矩阵 11 ''' 12 eclMat = M * before # M 变换 13 eclX = array(eclMat[0]).reshape(-1) 14 eclY = array(eclMat[1]).reshape(-1) 15 axis('equal') 16 axis([-3, 3, -3, 3]) 17 grid(True) 18 plot(eclX[:25], eclY[:25], 'c', linewidth=3) 19 plot(eclX[25:50], eclY[25:50], 'm', linewidth=3) 20 plot(eclX[50:75], eclY[50:75], 'y', linewidth=3) 21 plot(eclX[75:100], eclY[75:100], 'k', linewidth=3) 22 show() 23 return eclMat 24 25 26 ang = linspace(0, 2*pi, 100) 27 28 x = cos(ang) 29 y = sin(ang) 30 cirMat = matrix([x, y]) # 2 × 100 的圆圈矩阵 31 32 # 画最开始的图形——圆 33 plotCircle(cirMat) 34 35 # 画变换之后的椭圆 36 M = matrix([[2, 1], [1, 2]]) # 2 × 2 的变换矩阵 37 clMat = plotCircle(cirMat, M) 38 39 # 将 M 矩阵进行 svd 分解 40 U, s, V = np.linalg.svd(M, full_matrices=True) 41 S = np.diag(s) 42 43 # SVD 矩阵对圆的变换 44 plotCircle(cirMat) 45 Tran1 = plotCircle(cirMat, V) 46 Tran2 = plotCircle(Tran1, S) 47 Tran3 = plotCircle(Tran2, U)
3. SVD 向量空间
假设矩阵 A 的秩是 r, 那么对角线矩阵的秩也是 r (乘以酉矩阵不会改变矩阵的秩), 我们假设:

-
那么, Ax = 0 的 null space 也就是解空间是什么呢?答案如下:
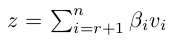
证明非常简单,直接带入 SVD 分解三个矩阵的右边,计算的时候正交的向量相乘都等于0, 不为 0 的恰好都被对角线矩阵的 0 元素归零,等号成立。如果 A 是列满秩的,显然符合条件的只剩下零向量了。同样的,你可以知道 A' 的 null space。 -
矩阵 A 的线性子空间是啥?设想有一个很高的矩阵 A, 它的列向量很有可能不是正交的。对于任意一个坐标 x,矩阵 A 的线性子空间可以定义为:
R(A) = {y | y = Ax, x 是任意的坐标}
那么, u1, u2,..., ur 是 R(A) 的正交基。
这个想法也非常直观,无论来了一个什么向量(或者叫坐标), 经过 V^T 和 对角线矩阵变换之后还是一个坐标,这个坐标就是 U 矩阵列向量线性组合的系数。
4. SVD 的计算
这就是正定矩阵的对角化。计算过程如下:
- 计算 A' (A 的转置)和 A'A
- 计算 A'A 的特征值,将特征值按照递减的顺序排列, 求均方根,得到 A 的奇异值
- 由奇异值可以构建出对角线矩阵 S, 同时求出 S 逆,以备后面的计算
- 有上述排好序的特征值可以求出对应的特征向量,以特征向量为列得到矩阵 V, 转置后得到 V'
- U = AVS逆,求出 U,完毕。
Lanczos algorithm 是一种迭代的计算方法,没来得及细看。
感觉 SVD 计算水很深,要用到的时候再看,现在暂不深入了。
5. PCA
主成分分析经常用于减少数据集的维数,同时保持数据集中的对方差贡献最大的特征。假设上面的椭圆中(二维空间,两个坐标值)均匀分布了非常多的点,如何在一维空间(一个坐标值)里面就能最大程度将这些点区分开来呢?这时候就要用到 PCA:

可以看到,上图中将所有的点投影到 +45° 直线上,将二维空间映射到一维空间,可以最大程度地区分开这些点,即投影后的样本分布方差最大,这个方向就是 v1 向量的方向。就上图来说,假设 100×2 的矩阵 X 表示样本点在平面上的坐标,将这些点投影到 v1 上保留最大的样本方差:
这样,就将 100 个 2 维空间的样本点压缩为 100 个 1 维空间的样本点,这里的列压缩实际上是对特征进行了压缩, 而不是简单地丢弃。PCA 是不是只能在样本点个数大于特征个数的时候才能压缩呢?例如,现在 3 个 100 维特征的样本用 100×3 的矩阵表示,用 SVD 分解后可以得到三个矩阵的乘积,做如下变换:
同样也最大限度保留了主成分。
总结起来,一个矩阵 A, 如果想对行进行压缩并保留主成分,那么左乘 u1', 如果相对列进行压缩并保留主成分(让我联想起了稀疏表示),那么右乘 v1。
当然,上面是简单的保留第一个主成分,PCA的全部工作简单点说,就是对原始的空间中顺序地找一组相互正交的坐标轴,第一个轴是使得方差最大的,第二个轴是在与第一个轴正交的平面中使得方差最大的,第三个轴是在与第1、2个轴正交的平面中方差最大的,这样假设在N维空间中,我们可以找到N个这样的坐标轴,我们取前r个去近似这个空间,这样就从一个N维的空间压缩到r维的空间了,但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。
6. 最小二乘问题
想法和 QR 分解的办法类似,主要是利用酉矩阵变换的长度不变性:
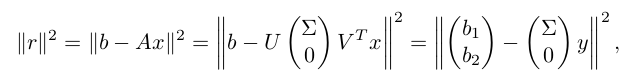
得到最优解是:
