(1)决策树的基本流程
决策树(decision tree):是一种基本的分类和回归方法。对于分类问题一般我们希望能够通过已有的数据来得到一个模型以对新的数据进行分类。而决策树是基于树的结构的,也是自然中常用的决策方法。比如说但银行判断能不能贷款给一个人时就采用的决策树的思维方式
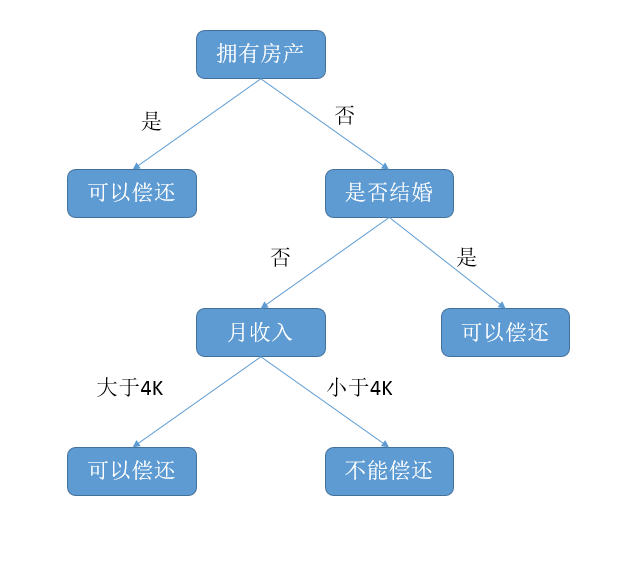
决策树的一般过程:(from http://www.cnblogs.com/tonglin0325/p/6050055.html)

决策树学习的基本算法:
输入:训练集 D={(x1,y1),(x2,y2),...,(xm,ym)} 属性集合 A={a1,a2....,ad}; 过程:函数TreeGenerate(D , A )
决策树的生成过程是一个递归过程:
首先给出递归终止条件:①当前节点所包含的样本全属于一个类别,例如此时{(xi,yi),(xi+1,yi+1)....}其中y相同;
②当前属性集合为空,或是所有样本在所有属性上取值相同,无法划分;(此时将该节点标为叶子节点,类型设定为其中y类型最多的)
③当前节点包含的样本集合为空,不能划分
当没有满足上述条件时:从A中选取最优划分属性a*,划分后继续对子节点递归;
(2)划分选择
从决策树的算法中可以看出最关键的是选取A中最优划分属性,这就要求我们找出最优划分属性;为了评价划分的优秀程度,也就是在划分中节点中包含的样本要尽可能的属于同一类别,就是说节点的纯度需要越来越高。
2.1 信息增益
信息熵(information entropy):度量样本纯度的工具;
在这里假设样本集合D中含有n个分类,第k个分类所占的比例为pk;则信息熵定义如下:

利用信息熵,我们可以刻画出一个数据集合的“纯度”,由公式可以看出当信息熵越小,则纯度越高。且信息熵最小为0,最大为log2(N)。
信息熵增益:既然可以刻画出纯度,那么我们可以利用穷举,分别计算出当使用不同属性分类后的节点信息熵,并采用加权相加方式得到总体的信息熵,那么使用不同属性得到的信息熵是不一样的,谁能使数据更“纯净”就采用谁来分类;
信息熵增益定义:

其中a是选取的离散属性,该属性有V中取值(a1,a2,...,av)。则使用a分类后会产生v个分支节点。每个分支节点的信息熵为


采用上式加权后相加就可以得到全局的信息熵。
目前采用信息熵增益的算法有: ID3决策树学习算法。
总结:信息熵增益的缺点:会对取值数目较多的属性有所偏好。(例如为每个样本编号,那编号这一属性一定是信息熵增益最高的,此时纯度最高)
2.2 增益率
为了解决信息增益方法的缺点,采用增益率的方法,就相当于除以属性取值的个数,这样就可以减少对取值较多的属性的偏好度。

IV(a)称为a的固定值,是描述a属性取值多少的一个固定值。
目前采用增益率的又C4.5决策树算法。
注意:采用增益率会对取值较少的属性有所偏好,因此C4.5算法并不是直接采用增益率,而是使用一个启发式,先选出信息增益高于平均水平的属性,再使用增益率选出最优划分属性。
4.2.基尼指数
数据集的纯度除了使用信息熵描述,还可以使用基尼值来描述。下面给出基尼值得计算公式:

Gini(D)反映出的是从数据集合中随机抽取出两个样本,其类别不一致的概率。因此纯度越高基尼值越低。
与信息熵相似,基尼值只是描述了数据集合的纯度,而用属性a划分后的基尼值,也就是该属性的基尼指数,定义如下:

在选取最优属性时,可以计算不同属性的基尼指数,从而找出基尼指数最小的作为最优划分属性。
采用基尼指数作为最优划分属性选择的算法有:“CART(Classification an Regression Tree)决策树算法”;
3.剪纸处理(防止过拟合)
过拟合是机器学习中最常见的错误,当你要识别一个叶子的时候,如果模型对叶子的每个叶脉都建模了那就是过拟合,在应对新的测试数据时就无法得到正确结果。
在决策树中,过拟合体现在一些不必要的分支的出现。因此要防止过拟合就得适当的剪枝,去除无法提高决策树泛化性能的分支。决策树中剪枝一般有两种策略:预剪枝,后剪枝。顾名思义,预剪枝是在建立决策树的过程中将一些无法提高泛化性能的分支剪去;后剪枝会在决策树建立之后再评测分支对泛化性能的影响决定是否剪枝。
3.1 预剪枝
要评价泛化性能可以将训练集合分为两个部分,一个部分用来训练,一部分用来进行预测和评价泛化性能。在采用一个最优属性选择策略后,我们可以得到决策树生成算法,预剪枝会在最优属性选择完毕之后,计算验证的精度,并与分支前对比。若精度变高则进行分支,否则不分支。
预剪枝优点:降低了过拟合的风险,还显著减少了决策树的训练书剑和测试时间
缺点:基于“贪心算法”的预剪枝,虽然当前分支无法提高泛化性能,但它之后的分支可能提高泛化性能。因此可能导致“欠拟合”,比如上面提到的叶子的例子,欠拟合就是将树识别为叶子。
3.2 后剪枝
后剪枝就是在建立决策树之后,从树的最低非叶子节点开始,先得出未剪枝的评价精度,然后计算出若采用子节点替换该子树后的精度,若精度提高或不变则剪枝,否则不剪枝。
后剪枝的优缺点:优点是减少了欠拟合的风险,泛化性能优于预剪枝。但是后剪枝因为要对非叶节点一一比较,训练的花费比预剪枝大得多。
4连续与缺失值的处理
4.1 连续属性的处理
上面提到的都是基于离散属性的,它的属性值有限可以穷举出来。但是对于连续属性,它的属性值的取值是无限的。这是要用到连续值离散化的技术。最简单的是C4.5决策树采用的二分法。
具体而言,就是将训练集中出现的连续属性数值排序后,选取其中位数作为划分点,也可以看做是离散属性的属性取值。再利用这些划分点计算信息增益。

注意:连续属性的划分与离散属性不同,该属性还可以作为其后代属性的划分属性。比如“密度《=0.5”,子节点可以使用“密度小于0.34”等等。
4.2缺失值的处理
在实际应用中,常常会遇到训练集合中一些值得某些属性值缺失的情况。这时如果简单的抛弃这些值是不恰当的,但是如何在这些值缺失的情况下进行最优划分属性的选取,与节点的划分是我们需要解决的两个问题。
首先是在值缺失的情况下选取最优划分属性。

在这里所有样本的初始权重都为1;
因此对于一个属性a , p表示的是无缺失样本所占的比例,pk表示的是无缺失样本中第k类样本所占的比例,第三个是在无缺失样本中某一属性值所占的比例。

至此我们可以根据带缺失值的数据集进行最优划分属性的选取。下面讨论如何划分属性值缺失的数据。
若样本x在a属性上的属性值缺失,则将x划入所有子节点,并用样本权重在于属性av对应的子节点中调整为rv*wx。也就是说让同一个数据样本以不同的概率划入不同的叶子节点。