飞行路线-洛谷4568

传送门

一道神仙题

（这题卡dijkstra啊哈哈

神仙的大佬秒出思路

神仙的大佬秒切

卑微的qxt de着if后面手欠打上去的‘；’的沙雕bug

我真开心...

-----------------------------------------------------------------------------------------------------------

题目描述

Alice和Bob现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在n个城市设有业务，设这些城市分别标记为0到n−1一共有m种航线，每种航线连接两个城市，并且航线有一定的价格。

Alice和Bob现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多k种航线上搭乘飞机。那么Alice和Bob这次出行最少花费多少？

输入输出格式

输入格式：

数据的第一行有三个整数，n,m,k，分别表示城市数，航线数和免费乘坐次数。
第二行有两个整数，s,t，分别表示他们出行的起点城市编号和终点城市编号。
接下来有m行，每行三个整数，a,b,c，表示存在一种航线，能从城市a到达城市b，或从城市b到达城市a，价格为c。

输出格式：

只有一行，包含一个整数，为最少花费。

输入输出样例

输入样例#1： 

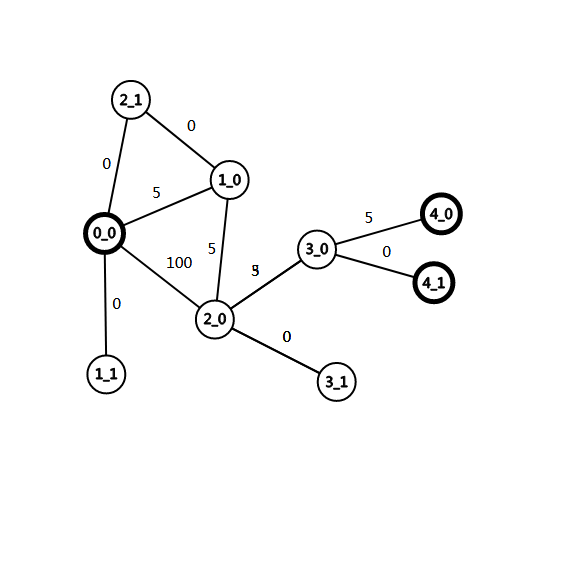
5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100

输出样例#1： 

8

说明

对于30%的数据,2≤n≤50,1≤m≤300,k=0;
对于50%的数据,2≤n≤600,1≤m≤6000,0≤k≤1;
对于100%的数据,2≤n≤10000,1≤m≤50000,0≤k≤10；

2018.12.10 增加一组 hack 数据

-----------------------------------------------------------------------------------------------------------

经典的分层图

（一脸懵）

对于图中的每个结点 u可以把它拆成 k+1个节点 u_j,j∈[0,k]

分别表示当使用 j次免费通行权限后到达 u 号节点的状态。

不一定要建这么多结点。只需要按照原始的输入建普通的图。

于是dijkstra就好了

（至于某位同学说的什么卡dijkstra什么的.我也不知道是怎么肥事）

（我就得没问题啊）

（显然，这题我也是膜了题解的）

#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#define INF 2147483647
#define N 20008
using namespace std;

inline int read()
{
    int sum = 0,p = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
            p = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        (sum *= 10) += ch - '0';
        ch = getchar();
    }
    return p * sum;
}

int n,m,k,s,t,cnt,ans = INF;
int dis[N][15];
bool vis[N][15];
struct edge
{
    int nxt,to,wei;
}e[N*6+5];
int head[N];

inline void add(int a,int b,int c)//加边 
{
    e[++cnt].nxt = head[a];
    e[cnt].to = b;
    e[cnt].wei = c;
    head[a] = cnt;
}

struct co
{
    int u,d,used;
    bool operator < (const co&a) const
    {
        return d > a.d;
    }
};

void dijkstra()
{
    memset(dis,127,sizeof(dis));
    dis[s][0] = 0;
    priority_queue<co>q;
    q.push((co){s,0,0});
    while(!q.empty())
    {
        int u = q.top().u;
        int now = q.top().used;
        q.pop();
        if(vis[u][now])
            continue;
        vis[u][now] = true;
        for(int i = head[u];i;i = e[i].nxt)
        {
            int o = e[i].to;
            if(now < k && !vis[o][now + 1] && dis[o][now + 1] > dis[u][now])
            {
                dis[o][now+1] = dis[u][now];
                q.push((co){o,dis[o][now+1],now+1});
            }
            if(!vis[o][now] && dis[o][now] > dis[u][now] + e[i].wei)
            {
                dis[o][now] = dis[u][now] + e[i].wei;
                q.push((co){o,dis[o][now],now});
            }
        }
    }
}

int main()
{
    n = read(),m = read(),k = read();
    s = read(),t = read();
    int a,b,c;
    for(int i = 1;i <= m;i++)
    {
        a = read(),b = read(),c = read();
        add(a,b,c);
        add(b,a,c);
    }
    dijkstra();
    for(int i = 0;i <= k;i++)
        ans = min(ans,dis[t][i]);
    printf("%d",ans);
    return 0;
}