双线性插值算法

1、介绍双线性插值算法前先讲下线性插值（Linear Interpolate)：

在数学中，线性插值是一种曲线拟合方法，利用线性多项式在已知数据点的离散集合范围内构造新的数据点。

两个已知点之间的线性插值：

已知两点由坐标(x0，y0)和(x1，y1)给出，线性插值就是两点之间的直线。对于区间(x0，x1)中的x值，由方程给出沿直线的y值

（1）

 

已知2点（x0,  y0)、(x1, y1)，

设线性方程：f(x) = ax + b

则有：

    y0 = f(x0)  = a * x0 + b;

    y1 = f(x1)  = a * x1 + b;

=>

y1 - y0 = a (x1 - x0)

得：a = (y1 - y0) / (x1 - x0)，a是斜率

y0 = a * x0 + b = (y1 - y0) / (x1 - x0)  * x0 + b

b = (x1 * y0 - x0 * y1) / (x1 - x0)

=>

y = f(x) = (y1 - y0) / (x1- x0) * x  +（x1 * y0 - x0 * y1) / (x1 - x0)

 

应用举例：D3.js的d3.interpolateRgb颜色插值原理应该用的是线性插值算法，根据RGB3个分量值的范围（0-255）分别进行线性插值。

 

2、双线性插值（Bilinear Interpolate)

在数学上，双线性插值是线性插值的拓展，是针对2维直线网格上的2个自变量函数z = f(x, y)的插值，涉及到2元函数，要复杂点。

主要思想是先在一个方向上执行线性插值，再在另一个方向上操作一次。虽然样本值和样本位置中的每一步插值是线性的，但是整体上是非线性的。

 

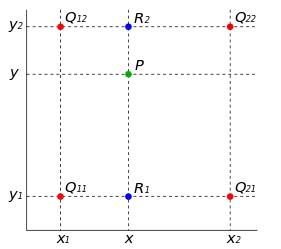
 注：红色点是原有的数据点，绿色点是我们想要插值的结果。

 

算法思路：

令我们要找的未知值的函数关系 f 和相应坐标（x, y)， 假设已知的4个点是Q11 = (x1, y1)，Q12=(x2, y2)，Q21=(x2, y1)， Q22=(x2, y2)。

首先在x轴上做线性插值，得到如下式子：

（2）

分析：

点R1是在Q11与Q21之间在x轴上进行一次线性插值的结果，y值都是y1不变。

f(x, y1) ≈ a * f(Q11) + b * f(Q21)

a = (x2 - x) / (x2 - x1),  b = (x - x1) / (x2 - x1)，这2个系数是如何确定的？

我认为和点的（x, y)位置相关，Q11、Q21对点R1的值f(x, y1)的影响程度取决于它们和R1点的距离值，也就是|x - x1|和|x2 - x|，谁与点R1距离近，影响程度越大，也就是相应的系数越大。

总的距离为| x2 - x1|，即点Q11与Q21之间的距离D， R1距离Q11为d1 = |x - x1|,   R1距离Q21为d2 = |x2 - x|，且R1位于Q11与Q21之间，即 x1 < x < x2,  当d1减小时，d2会变大，而此时Q11的相关系数a应该变大，Q21的相关系数b应变小，观察发现d1/D会随着d1变小而变小，d2 = D-d1,  d2/D会随着d1变小而变大，因此a = d2/D = (x2 - x) / (x2 - x1)，b = (x - x1) / (x2 - x1)，这样a * f(Q11)在随R1靠近点Q11而变大，b * f(Q21)随R11远离Q21而变小，满足条件。

 

 

我们继续在y轴上插值得到估算式子：

（3）

注：先在x轴还是y轴上插值的最终结果是一致的，顺序不影响插值结果。

 

上面的代数式比较繁，我们可以用矩阵来求解，以达到化繁为简。

设二元函数如下：

代入四个已知点，系数a0,a1,a2,a3可以通过解线性系统得到：

若一个解用f(Q)表示，我们可以写成：

  （4）

推导：

       a0 + a1 * x + a2 * y + a3 * xy = b11 * f(Q11) + b12 * f(Q12) + b21 * f(Q21) + b22 * f(Q22)

=>  

 

 =>

 =>

 

=>

   =>

=>

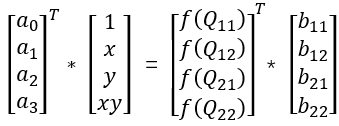
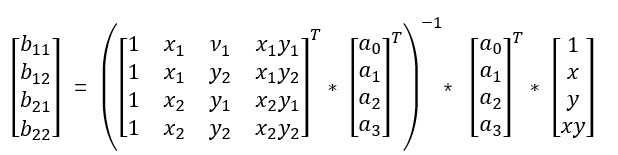
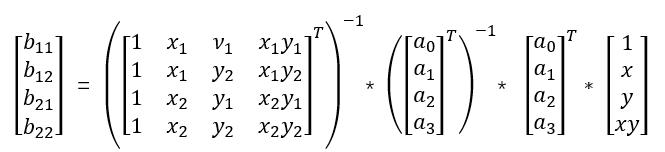
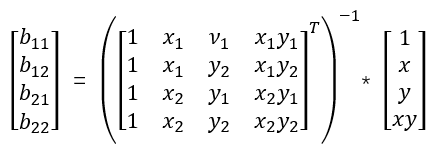
  得出最终式子：

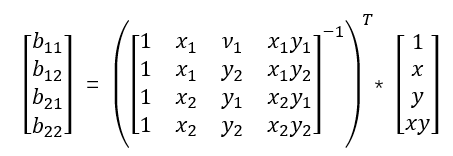（5）

系数可以通过解线性系统获得。

若用一个坐标系来表示Q11 =（0，0）、Q12 =（0，1）、Q21 =（1， 0）、Q22 =（1， 1）四个已知的点，则插值公式可以简化为：

（6）

 上面的式子可以直接把坐标代入式子（3）得到，也可以解式子（5）矩阵求得系数b11、b12、b21、b22,再代入（4）得到，计算过程如下（复习下线性代数）：

复习：矩阵A的逆矩阵A^-1可以用高斯若尔当消元法；A*A^-1 = I（单位矩阵）； (A^-1)^T = (A^T)^-1。

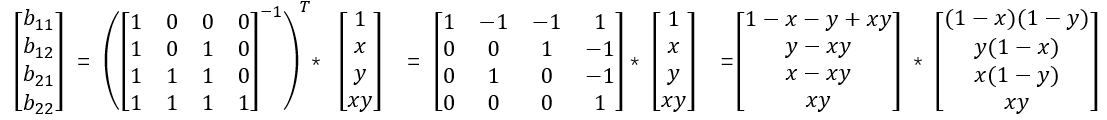
得：b11 = (1 - x) * (1 - y)， b12 = y * (1 - y) ,  b21 = x * (1 - y) , b22 = xy

f(x, y) = b11 * f(Q11) + b12 * f(Q12) + b21 * f(Q21) + b22 * f(Q22) = (1 - x) * (1 - y) * f(0, 0) + y * (1 - x) * f(0, 1) + x * (1 - y) * f(1, 0) + xy * f(1, 1)， 整理即为式（6）

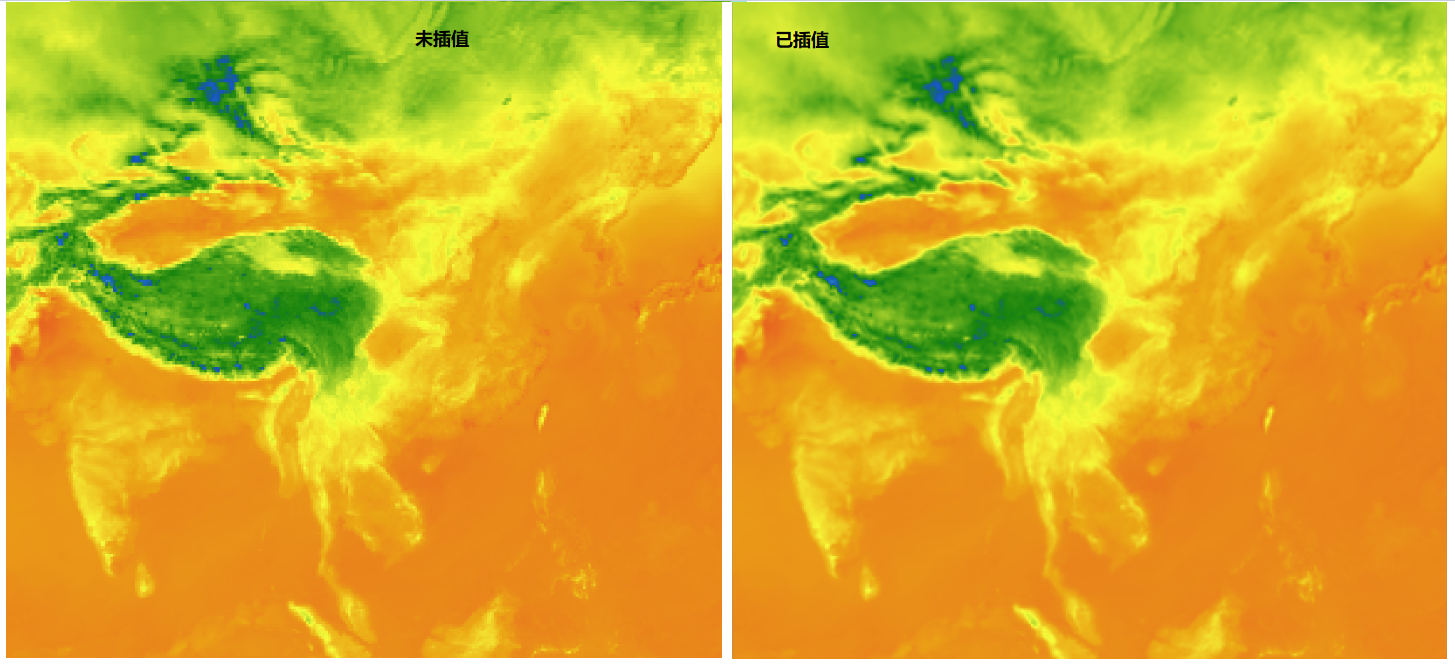
 3、双线性插值算法应用：对NCEP气象数据使用双线性插值以增加数据的稠密度，改善绘制的气象图谱效果。

温度分布图绘制：

 /**
     * 直接根据原始数据绘制，不插值
     */
    private void drawGridsWithoutInterpolation(){
        int x = 0, xMax = this.imgWidth, y = 0, yMax = this.imgHeight;
        int nx = this.entity.getNx();
        int ny = this.entity.getNy();
        double lo1 = this.entity.getLo1();
        double lo2 = this.entity.getLo2();
        double la1 = this.entity.getLa1();
        double la2 = this.entity.getLa2();
        double deltLO = lo2 - lo1;
        double deltLA = la2 - la1;
        Double[] data = this.entity.getData();
        double[] color = {0, 0, 0, 0}; //Transparent black
        for(int i=x; i<xMax; i++) {
            for(int j=y; j<yMax; j++){
                Point p = CRSutil.toPoint(i, j);
                p = p.add(this.pixelOrigin);
                LngLat lnglat = this.crs.pixelPointToLngLat(p);
                double lng = lnglat.lng;
                double lat = lnglat.lat;
                int col = (int) Math.floor((lng -lo1)/deltLO * nx);
                int row = (int) Math.floor((lat -la1)/deltLA * ny);
                if(col<0) {
                    col = 0;
                }
                if(col>=xMax){
                    col = xMax-1;
                }
                if(row<0){
                    row = 0;
                }
                if(col>=yMax){
                    row = yMax - 1;
                }
                int index = row * nx + col;
                double value = data[index];
                color = this.scale.getPointColor(value, OVERLAY_ALPHA);
                drawGrid(i, j, color);
                drawGrid(i+1, j, color);
                drawGrid(i, j+1, color);
                drawGrid(i+1, j+1, color);
            }
        }

    }
    

 /**
     * 先插值再绘制
     */
    private void interpolateField() {
        int x = 0, xMax = this.imgWidth, y = 0, yMax = this.imgHeight;
        Double scalar = 0d;
        double[] color = {0, 0, 0, 0}; //Transparent black
        for(int i=x; i<xMax; i+=2) {
            for(int j=y; j<=yMax; j+=2) {
               Point p = CRSutil.toPoint(i, j);
               p = p.add(this.pixelOrigin);
               LngLat lnglat = this.crs.pixelPointToLngLat(p);
               if(this.entity.getMeteoType().equals(MeteoTypeEnum.WIND)){
                    //TODO
               }else{
                  scalar = interpolate(lnglat, this.grid);
                  if(scalar==null){
                      continue;
                  }
                  color = this.scale.getPointColor(scalar, OVERLAY_ALPHA);
                //   logger.info(scalar+"--"+color[0]+","+color[1]+","+color[2]+","+color[3]);
                  drawGrid(i, j, color);
                  drawGrid(i+1, j, color);
                  drawGrid(i, j+1, color);
                  drawGrid(i+1, j+1, color);
               }
            }
        }

    }

效果图对比：