枚举、二进制、双精度精度等问题

1.对于枚举类型

package LianXi;

public class EnumTest {

    public static void main(String[] args) {
        Size s=Size.SMALL;
        Size t=Size.LARGE;
        //s和t引用同一个对象？
        System.out.println(s==t);  //
        //是原始数据类型吗？
        System.out.println(s.getClass().isPrimitive());
        //从字符串中转换
        Size u=Size.valueOf("SMALL");
        System.out.println(s==u);  //true
        //列出它的所有值
        for(Size value:Size.values()){
            System.out.println(value);
        }
    }

}
 enum Size{SMALL,MEDIUM,LARGE};

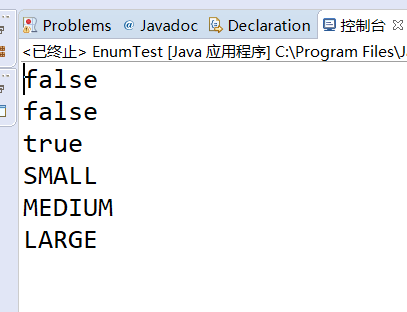
对于枚举类型它的每个具体值都引用一个特定的对象。相同的值则引用同一个对象。并且==与equals

2.局部变量和全局变量

package LianXi;
public class lianXi {
    private static int a=897;
public static void main(String []args){
    int a=3636;
    System.out.println(a);
    //System.out.print(a/0);
    }
}

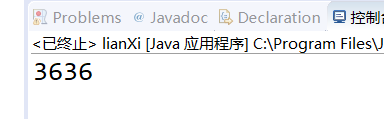
局部变量可以屏蔽全局变量

3.关于精度的实验测试

package LianXi;
public class TestDouble {
    public static void main(String args[]) {
        System.out.println("0.05 + 0.01 = " + (0.05 + 0.01));
        System.out.println("1.0 - 0.42 = " + (1.0 - 0.42));
        System.out.println("4.015 * 100 = " + (4.015 * 100));
        System.out.println("123.3 / 100 = " + (123.3 / 100));
    }
}
//尾数不一样（浮点数的运算精度）

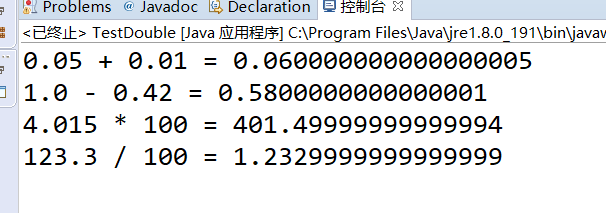
 得出的结论使用double类型的数值进行计算， 其结果是不精确的。Double类型的数值占用64bit，即64个二进制数，除去最高位表示正负符号的位，在最低位上一定会与实际数据存在误差（除非实际数据恰好是2的n次方）。

4.关于输出中的“+”

package LianXi;
public class TestDouble {
    public static void main(String args[]) {
        int X=100;
        int Y=200;
        System.out.println("X+Y="+X+Y);
        System.out.println(X+Y+"=X+Y");
    }
}
//尾数不一样（浮点数的运算精度）

“+”号运算符结合顺序是从左到右，当前面没有字符串时如果是用“+”连接两个数字将进行先运算在输出。

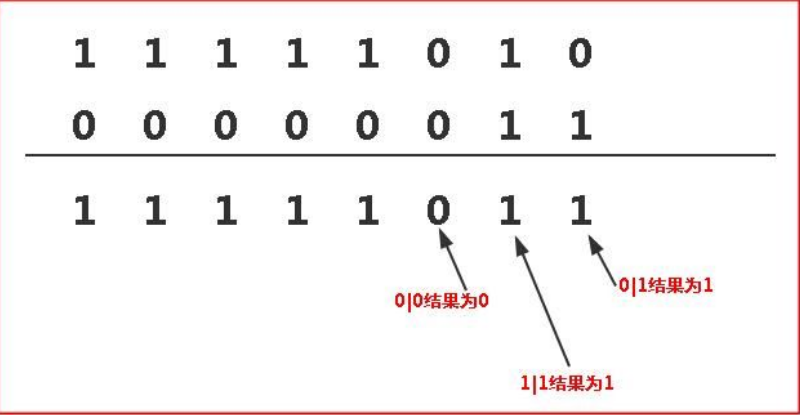
5.关于二进制的问题

正数的原码补码和反码都相等

负数：原码就是原来的表示方法反码是除符号位（最高位）外取反补码=反码+1

使用二制数中的最高位表示正负。

package LianXi;
public class TestDouble {
public static void main(String args[]) {
int x=18;
System.out.println(x<<3);
System.out.println(x>>3);
System.out.println(x>>>3);
System.out.println(~x);
System.out.println(x&3);
System.out.println(x|3);
int y=-18;
System.out.println(y<<3);
System.out.println(y>>3);
System.out.println(y>>>3);
System.out.println(~y);
System.out.println(y&3);
System.out.println(y|3);
}
}

}

这是关于二进制的相关操作。

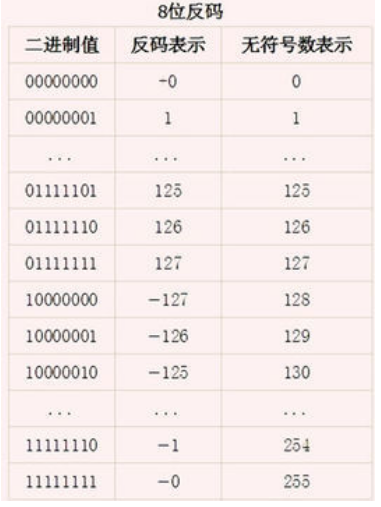
例如，当编码总位数为8时有：

+127的原码、反码、补码都为：0 1111111。

-127的原码、反码、补码依次为：1 1111111、1 0000000、1 0000001。

+0、-0的原码分别为：0 0000000、1 0000000，均对应真值0。

将128化为二进制为：1 0000000，最高位为1，可以只对舍去最高位后剩余的7位进行处理即可，首先取反得：1111111，加1得：1 0000000，最高位有进位需丢弃，即得：0000000，加上符号位就得补码：1 0000000。

又如，当编码总位数为4时，真值X=+0.101的原码、反码、补码均为：0 101。

真值X=-0.101的原码、反码、补码依次为：1 101、1 010、1 011。

同理，特例，-1的补码为：1 000。

在定点小数中，小数点隐含在第一位编码和第二位编码之间。

相关知识：

在计算器中参与运算的数有两大类：无符号数和有符号数

     (1)有符号数：

          对于有符号数而言，符号的正、负机器是无法识别的，但由于“正、负”恰好是两种截然不同的状态，如果用“0”表示“正”，用“1”表示“符”，这样符号也被数字化了，

          并且规定将它放在有效数字的前面，即组成了有符号数。所以，在二进制中使用最高位（第一位）来表示符号，最高位是0，表示正数；最高位是1，表示负数。

     (2)无符号数：

          无符号数是针对二进制来讲的，无符号数的表数范围是非负数。全部二进制均代表数值（所有位都用于表示数的大小），没有符号位。即第一个"0"或"1"不表示

          正负。