傅立叶变换在图像处理中有非常重要的作用。因为不仅傅立叶分析涉及图像处理很多方面,傅立 叶改进算法,比如离散余弦变换,gabor与小波在图像处理中也有重要的分量。傅立叶变换在图像处理的重要作用:
1.图像增强与图像去噪
绝 大部分噪音都是图像的高频分量,通过低通滤波器来滤除高频——噪声; 边缘也是图像的高频分量,可以通过添加高频分量来增强原始图像的边缘;
2.图像分割之边缘检测
提 取图像高频分量
3.图像特征提取:
形状特征:傅里叶描述子
纹 理特征:直接通过傅里叶系数来计算纹理特征
其他特征:将提取的特征值进行傅里叶变 换来使特征具有平移、伸缩、旋转不变性
4.图像压缩
可以直接通过傅里叶系数来压缩数据;常用的离散余弦变换是傅立叶变换的实变换;傅立叶变换。
傅里叶变换是将 时域信号分解为不同频率的正弦信号或余弦函数叠加之和。连续情况下要求原始信号在一个周期内满足绝对可积条件。离散情况下,傅里叶变换一定存在。冈萨雷斯 版<图像处理>里面的解释非常形象:一个恰当的比喻是将傅里叶变换比作一个玻璃棱镜。棱镜是可以将光分解为不同颜色的物理仪器,每个成分的颜 色由波长(或频率)来决定。傅里叶变换可以看作是数学上的棱镜,将函数基于频率分解为不同的成分。当我们考虑光时,讨论它的光谱或频率谱。同样,傅立叶变 换使我们能通过频率成分来分析一个函数。
傅立叶变换有很多优良的性质。
如线性, 对称性(可以用在计算信号的傅里叶变换里面);
时移性:函数在时域中的时移,对 应于其在频率域中附加产生的相移,而幅度频谱则保持不变;
频移性:函数在时域中乘 以e^jwt,可以使整个频谱搬移w。这个也叫调制定理,通讯里面信号的频分复用需要用到这个特性(将不同的信号调制到不同的频段上同时传输);
卷积定理:时域卷积等于频域乘积;时域乘积等于频域卷积(附加一个系数)。(图像处理里面 这个是个重点)。
信号在频率域的表现。
在频域中,频率越大说明原始信号变化速度越快;频率越小说明原始信号越平缓。当频率为0时,表示直 流信号,没有变化。因此,频率的大小反应了信号的变化快慢。高频分量解释信号的突变部分,而低频分量决定信号的整体形象。
在图像处理中,频域反应了图像在空域灰度变化剧烈程度,也就是图像灰度的变化速度,也就是图像的梯 度大小。对图像而言,图像的边缘部分是突变部分,变化较快,因此反应在频域上是高频分量;图像的噪声大部分情况下是高频部分;图像平缓变化部分则为低频分 量。也就是说,傅立叶变换提供另外一个角度来观察图像,可以将图像从灰度分布转化到频率分布上来观察图像的特征。书面一点说就是,傅里叶变换提供了一条从 空域到频率自由转换的途径。对图像处理而言,以下概念非常的重要:
图像高频分量: 图像突变部分;在某些情况下指图像边缘信息,某些情况下指噪声,更多是两者的混合;
低 频分量:图像变化平缓的部分,也就是图像轮廓信息
高通滤波器:让图像使低频分量抑 制,高频分量通过
低通滤波器:与高通相反,让图像使高频分量抑制,低频分量通过
带通滤波器:使图像在某一部分的频率信息通过,其他过低或过高都抑制
带阻滤波器,是带通的反。
模板运算与卷积定理
在时域内做模板运算,实际上就是对图像进行卷积。 模板运算是图像处理一个很重要的处理过程,很多图像处理过程,比如增强/去噪(这两个分不清楚),边缘检测中普遍用到。根据卷积定理,时域卷积等价与频域 乘积。因此,在时域内对图像做模板运算就等效于在频域内对图像做滤波处理。
比如说 一个均值模板,其频域响应为一个低通滤波器;在时域内对图像作均值滤波就等效于在频域内对图像用均值模板的频域响应对图像的频域响应作一个低通滤波。
图像去噪
图像去噪 就是压制图像的噪音部分。因此,如果噪音是高频额,从频域的角度来看,就是需要用一个低通滤波器对图像进行处理。通过低通滤波器可以抑制图像的高频分量。 但是这种情况下常常会造成边缘信息的抑制。常见的去噪模板有均值模板,高斯模板等。这两种滤波器都是在局部区域抑制图像的高频分量,模糊图像边缘的同时也 抑制了噪声。还有一种非线性滤波-中值滤波器。中值滤波器对脉冲型噪声有很好的去掉。因为脉冲点都是突变的点,排序以后输出中值,那么那些最大点和最小点 就可以去掉了。中值滤波对高斯噪音效果较差。
椒盐噪声:对于椒盐采用中值滤波可以 很好的去除。用均值也可以取得一定的效果,但是会引起边缘的模糊。
高斯白噪声:白 噪音在整个频域的都有分布,好像比较困难。
冈萨雷斯版图像处理P185:算术均值 滤波器和几何均值滤波器(尤其是后者)更适合于处理高斯或者均匀的随机噪声。谐波均值滤波器更适合于处理脉冲噪声。
图像增强
有时候感觉图像增 强与图像去噪是一对矛盾的过程,图像增强经常是需要增强图像的边缘,以获得更好的显示效果,这就需要增加图像的高频分量。而图像去噪是为了消除图像的噪 音,也就是需要抑制高频分量。有时候这两个又是指类似的事情。比如说,消除噪音的同时图像的显示效果显著的提升了,那么,这时候就是同样的意思了。
常见的图像增强方法有对比度拉伸,直方图均衡化,图像锐化等。前面两个是在空域进行基于像 素点的变换,后面一个是在频域处理。我理解的锐化就是直接在图像上加上图像高通滤波后的分量,也就是图像的边缘效果。对比度拉伸和直方图均衡化都是为了提 高图像的对比度,也就是使图像看起来差异更明显一些,我想,经过这样的处理以后,图像也应该增强了图像的高频分量,使得图像的细节上差异更大。同时也引入 了一些噪音。
对图像二维傅立叶变换的意义
众所周至,傅立叶变换可以将连续或离散的函数序列从空域映射到频域上,因此,傅立叶变换是信息与信号学中不可获缺的强大工具。但是,由于傅立 叶变换在学习时是以一大堆公式的形式给出的,因此很多人(包括我在内)往往在做了一大堆习题掌握了变换的数学表示却对其变换后的物理意义一无所知,尤其是 自学的时候更是晕头转向。
这里假设大家对傅立叶变换的数学表示已经很熟悉了,撇开傅立叶变换本身和其在其他领域的应用不谈,只谈图像傅立叶变换前后的对应关系。我们知道傅立叶变换 以前,图像(未压缩的位图)是由对在连续空间(现实空间)上的采样得到一系列点的集合,我们习惯用一个二维矩阵表示空间上各点,则图像可由 z=f(x,y)来表示。由于空间是三维的,图像是二维的,因此空间中物体在另一个维度上的关系就由梯度来表示,这样我们可以通过观察图像得知物体在三维 空间中的对应关系。为什么要提梯度?因为实际上对图像进行二维傅立叶变换得到频谱图,就是图像梯度的分布图,当然频谱图上的各点与图像上各点并不存在一一 对应的关系,即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一的亮点,实际上图像上某一点与邻域点差异的强弱,即梯度的大小,也即该点的 频率的大小(可以这么理解,图像中的低频部分指低梯度的点,高频部分相反)。一般来讲,梯度大则该点的亮度强,否则该点亮度弱。这样通过观察傅立叶变换后 的频谱图,也叫功率图(看看频谱图的各点的计算公式就知道为什么叫功率图了:)),我们首先就可以看出,图像的能量分布,如果频谱图中暗的点数更多,那么 实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小),反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的,边界分明且边界两边像素差 异较大的。对频谱移频到原点以后,可以看出图像的频率分布是以原点为圆心,对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外,还有一个好 处,它可以分离出有周期性规律的干扰信号,比如正玄(sin的正玄,找不到这个字,郁闷)干扰,一副带有正玄干扰,移频到原点的频谱图上可以看出除了中心 以外还存在以某一点为中心,对称分布的亮点集合,这个集合就是干扰噪音产生的,这时可以很直观的通过在该位置放置带阻滤波器消除干扰。
1.使用模板处理图像相关概念:
模板:矩阵方块,其数学含义是一种卷积运算。
卷积运算:可看作是加权求和的过程,使用到的图像区域中的每个像素分别于卷积核(权矩阵)的每个元素对应相
乘,所有乘积之和作为区域中心像素的新值。
卷积核:卷积时使用到的权用一个矩阵表示,该矩阵与使用的图像区域大小相同,其行、列都是奇数,
是一个权矩阵。
卷积示例:
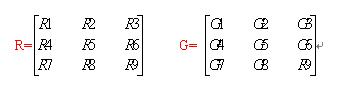
3 * 3 的像素区域R与卷积核G的卷积运算:
R5(中心像素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
2.使用模板处理图像的问题:
边界问题:当处理图像边界像素时,卷积核与图像使用区域不能匹配,卷积核的中心与边界像素点对应,
卷积运算将出现问题。
处理办法:
A. 忽略边界像素,即处理后的图像将丢掉这些像素。
B. 保留原边界像素,即copy边界像素到处理后的图像。
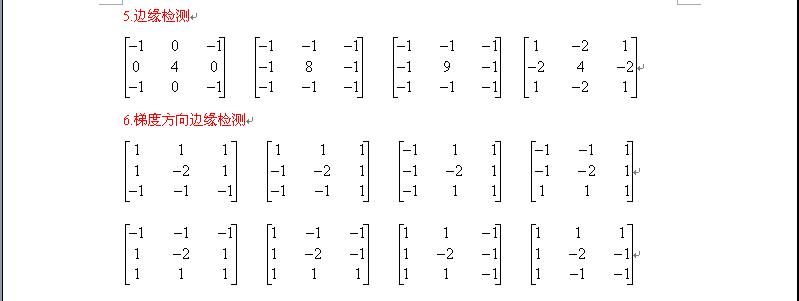
3.常用模板:
http://blog.csdn.net/abcjennifer/article/details/7622228
http://cns-alumni.bu.edu/~slehar/fourier/fourier.html#filtering
https://blog.csdn.net/m0_37264397/article/details/70186390