使用深度优先搜索查找路径

给定图G及起点s，查找从s到其他顶点的路径。

设计一个类实现该算法，类的API如下：

基于深度优先搜索实现路径查找，该算法扩展深度优先搜索，在原算法的基础上添加一个实例变量edgeTo[]，这个数组用于记录每个与s连通的顶点回到s的路径。

 如下图：

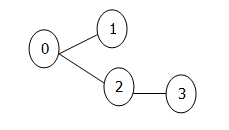
edgeTo[]的值为：

节点1与2（数组下标表示节点）存储的为0，表示由节点1或2可以到节点0，节点3存储的为2，表明节点3可以到节点2 。那么由节点0到节点3的路径为0-2-3。

实现代码如下：

public class DepthFirstPaths {

    private int s;
    private boolean[] marked;
    private int[] edgeTo;

    public DepthFirstPaths(Graph G, int s) {
        this.s = s;
        marked = new boolean[G.V()];
        edgeTo = new int[G.V()];
        dfs(G, s);
    }

    private void dfs(Graph G, int v) {
        marked[v] = true;
        for (int w:G.adj(v)) {
            if (!marked[w]) {
                edgeTo[w] = v;
                dfs(G, w);
            }
        }
    }

    public boolean hasPathTo(int v) {
        return marked[v];
    }


    public Iterable<Integer> pathTo(int v) {
        if (!marked[v]) return null;
        Stack<Integer> path = new Stack<>();
        for (int x = v; x != s; x = edgeTo[x])
            path.push(x);
        path.push(s);
        return path;
    }

}

示例：

如下图，使用深度优先搜索查找G中顶点0到其他顶点路径的过程及结果

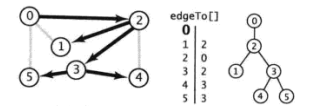
    public static void main(String[] args) {

        Graph G = new Graph(6);
        G.addEdge(0, 5);
        G.addEdge(0, 1);
        G.addEdge(0, 2);
        G.addEdge(2, 4);
        G.addEdge(2, 3);
        G.addEdge(2, 1);
        G.addEdge(3, 4);
        G.addEdge(3, 5);

        DepthFirstPaths paths = new DepthFirstPaths(G, 0);
        for (int x:paths.pathTo(5))
            System.out.print(x + " ");
        System.out.println();

    }