题目来源:http://poj.org/problem?id=1024
题目大意:
有一个迷宫,迷宫的起点在(0,0)处。给定一条路径,和该迷宫墙的设置,要求验证该路径是否为唯一的最短路径,该种墙的设置中是否存在多于的墙,可结合图进行理解。
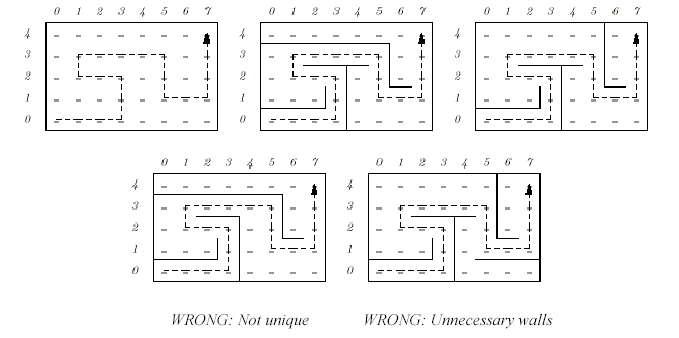
输入:第一行制定测试用例数。每个测试用例的第一行为两个正整数,指明迷宫的长和宽。接下来是给定的最短路径,用由L(左)R(右)U(上)D(下)组成的字符串表示。然后输入一个正整数m表示墙的个数。后接m行,每行四个整数,前两个整数和后两个整数分别组成两个坐标,表示该面墙把这两个点之间的路径隔断。
输出:若符合条件输出CORRECT否则输出INCORRECT。
Sample Input
2 8 5 RRRUULLURRRRDDRRUUU 19 0 0 0 1 1 0 1 1 2 0 2 1 2 1 3 1 3 0 4 0 3 1 4 1 3 2 4 2 3 2 3 3 2 2 2 3 4 2 4 3 0 3 0 4 1 3 1 4 2 3 2 4 3 3 3 4 4 3 4 4 5 3 5 4 5 3 6 3 5 2 6 2 6 1 6 2 4 3 RRRUU 2 2 2 3 2 2 2 2 1
Sample Output
CORRECT INCORRECT
一开始没有什么想法,看了Discuss里的讨论和一些解题报告,思路很高明。
1. bfs求各点到源点的最小步数
2. bfs求各点到终点的最小步数
3. 遍历所有网格点,如果某不在路径上的点,到源点的步数+到终点的步数<=给定的路径,则给定的路径不是唯一最短
4. 检查每堵墙,如果把墙两侧点 到起点和到终点的步长加起来+1 > 给定路径的长度,则该墙多余。(如果拆掉这堵墙,唯一最短路径不变就说明多余)

1 ////////////////////////////////////////////////////////////////////////// 2 // POJ1024 Tester Program 3 // Memory: 368K Time: 16MS 4 // Language: C++ Result: Accepted 5 ////////////////////////////////////////////////////////////////////////// 6 7 #include <iostream> 8 #include <string> 9 #include <queue> 10 using namespace std; 11 12 struct Grid { 13 bool inpath; // 是否是路径方格 14 bool uwal; // 是否有上墙 15 bool rwal; // 是否有右墙 16 int scnt; // 到源点步数 17 int dcnt; // 到终点步数 18 }; 19 20 int main(void) { 21 bool ok; 22 int w, h, cnt, steps; // 1 <= w, h <= 100 23 string path; 24 Grid grid[100][100]; 25 queue<pair<int, int> > q; 26 27 int t, x, y, desx, desy, x2, y2, i; 28 for (cin >> t; t > 0; --t) { 29 //初始化数据 30 cin >> w >> h; 31 for (y = 0; y < h; ++y) { 32 for (x = 0; x < w; ++x) { 33 grid[y][x].inpath = false; 34 grid[y][x].uwal = false; 35 grid[y][x].rwal = false; 36 grid[y][x].scnt = -1; 37 grid[y][x].dcnt = -1; 38 } 39 } 40 cin >> path; 41 x = 0, y = 0; 42 grid[0][0].inpath = true; 43 steps = path.size(); 44 for (i = 0; i < steps; ++i) { 45 switch (path[i]) { 46 case 'U': ++y; break; 47 case 'D': --y; break; 48 case 'L': --x; break; 49 case 'R': ++x; break; 50 } 51 grid[y][x].inpath = true; 52 } 53 desx = x, desy = y; 54 cin >> cnt; 55 for (i = 0; i < cnt; ++i) { 56 cin >> x >> y >> x2 >> y2; 57 if (x == x2) 58 if (y + 1 == y2) grid[y][x].uwal = true; 59 else grid[y2][x].uwal = true; 60 else 61 if (x + 1 == x2) grid[y][x].rwal = true; 62 else grid[y][x2].rwal = true; 63 } 64 65 //求各点到源点的最小步数(BFS) 66 q.push(make_pair(0, 0)); 67 grid[0][0].scnt = 0; 68 while (!q.empty()) { 69 y = q.front().first, x = q.front().second; 70 if (y < h - 1 && grid[y][x].uwal == false && grid[y + 1][x].scnt == -1) { 71 grid[y + 1][x].scnt = grid[y][x].scnt + 1; 72 q.push(make_pair(y + 1, x)); 73 } 74 if (0 < y && grid[y - 1][x].uwal == false && grid[y - 1][x].scnt == -1) { 75 grid[y - 1][x].scnt = grid[y][x].scnt + 1; 76 q.push(make_pair(y - 1, x)); 77 } 78 if (0 < x && grid[y][x - 1].rwal == false && grid[y][x - 1].scnt == -1) { 79 grid[y][x - 1].scnt = grid[y][x].scnt + 1; 80 q.push(make_pair(y, x - 1)); 81 } 82 if (x < w - 1 && grid[y][x].rwal == false && grid[y][x + 1].scnt == -1) { 83 grid[y][x + 1].scnt = grid[y][x].scnt + 1; 84 q.push(make_pair(y, x + 1)); 85 } 86 q.pop(); 87 } 88 89 //求各点到终点的最小步数(BFS) 90 q.push(make_pair(desy, desx)); 91 grid[desy][desx].dcnt = 0; 92 while (!q.empty()) { 93 y = q.front().first, x = q.front().second; 94 if (y < h - 1 && grid[y][x].uwal == false && grid[y + 1][x].dcnt == -1) { 95 grid[y + 1][x].dcnt = grid[y][x].dcnt + 1; 96 q.push(make_pair(y + 1, x)); 97 } 98 if (0 < y && grid[y - 1][x].uwal == false && grid[y - 1][x].dcnt == -1) { 99 grid[y - 1][x].dcnt = grid[y][x].dcnt + 1; 100 q.push(make_pair(y - 1, x)); 101 } 102 if (0 < x && grid[y][x - 1].rwal == false && grid[y][x - 1].dcnt == -1) { 103 grid[y][x - 1].dcnt = grid[y][x].dcnt + 1; 104 q.push(make_pair(y, x - 1)); 105 } 106 if (x < w - 1 && grid[y][x].rwal == false && grid[y][x + 1].dcnt == -1) { 107 grid[y][x + 1].dcnt = grid[y][x].dcnt + 1; 108 q.push(make_pair(y, x + 1)); 109 } 110 q.pop(); 111 } 112 113 //判断路径是否唯一最短,以及墙是否多余 114 ok = true; 115 for (y = 0; y < h && ok; ++y) { 116 for (x = 0; x < w && ok; ++x) { 117 if (grid[y][x].scnt == -1 || grid[y][x].dcnt == -1) 118 ok = false; // 是否有封闭区域 119 if (y < h - 1 && grid[y][x].uwal 120 && grid[y][x].scnt + grid[y + 1][x].dcnt + 1 > steps 121 && grid[y][x].dcnt + grid[y + 1][x].scnt + 1 > steps) 122 ok = false; // 是否上墙多余 123 if (x < w - 1 && grid[y][x].rwal 124 && grid[y][x].scnt + grid[y][x + 1].dcnt + 1 > steps 125 && grid[y][x].dcnt + grid[y][x + 1].scnt + 1 > steps) 126 ok = false; // 是否右墙多余 127 if (!grid[y][x].inpath && grid[y][x].scnt + grid[y][x].dcnt <= steps) 128 ok = false; // 是否存在更短路径或另一最短路径 129 } 130 } 131 if(ok) cout << "CORRECT" << endl; 132 else cout << "INCORRECT" << endl; 133 } 134 return 0; 135 }
