numpy是一个在Python中做科学计算的基础库,重在数值计算,也是大部分PYTHON科学计算库的基础库,多用于在大型、多维数组上执行数值运算。
数组的定义
import numpy as np
# numpy数组的定义方法
a = np.arange(1, 6, 2)
b = np.array([1, 3, 5])
c = np.array(range(1, 6, 2))
# 这样产生的a,b,c三个结果是一样的,均为[1, 3, 5]
# 这里看一下数组的类型和数组元素的类型的定义和修改,type(a)表示的是数组a的类型,a.dtype则表示的是数组a中元素的类型。
In [1]: import numpy as np
In [2]: a = np.array([1, 2, 3])
In [3]: print(a, type(a), a.dtype)
[1 2 3] <class 'numpy.ndarray'> int32
In [4]: a = np.array([1, 2, 3], dtype = "float64")
In [5]: print(a, type(a), a.dtype)
[1. 2. 3.] <class 'numpy.ndarray'> float64
In [6]: a = a.astype("int64")
In [7]: print(a, type(a), a.dtype)
[1 2 3] <class 'numpy.ndarray'> int64
#要保留固定位数的小数需要用到np.round()
In [1]: import random
In [2]: import numpy as np
In [3]: "%.2f"%random.random()
Out[3]: '0.56'
In [4]: round(random.random(), 2)
Out[4]: 0.73
In [5]: a = np.round(np.array([random.random() for i in range(10)]), 2)
In [6]: a
Out[6]: array([0.7 , 0.95, 0.6 , 0.03, 0.27, 0.96, 0.17, 0.48, 0.3 , 0.23])
In [7]: np.round(a, 1)
Out[7]: array([0.7, 1. , 0.6, 0. , 0.3, 1. , 0.2, 0.5, 0.3, 0.2])
数组的形状
以下的代码是在Jupyter Notebook中完成的:
# 数组的形状
In [1]: import numpy as np
In [2]: a = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
In [3]: a
Out[3]: array([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]])
In [4]: a.shape
Out[4]: (2, 2, 3)
# 上面元组中的元素个数即是这个数组的维数,例如这个就是个三维数组,他一共有 2 块,每块有 2 行, 3 列,即(2, 2, 3)
In [5]: a.reshape((3, 4))
Out[5]: array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
In [6]: a.reshape((12,))
Out[6]: array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
In [7]: a
Out[7]: array([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]])
# 从这里看以看出a.reshape并不能改变a的形状和维度,如果需要改变a的维度和形状,需要重新对a进行赋值,如下↓:
In [8]: a = a.reshape((4,3))
In [9]: a
Out[9]: array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
# 计算一个二维数组的元素个数,可以使用如下的方法,shape[0]是这个二维数组的行数,shape[1]即是这个数组的列数。
In [10]: a.shape[0] * a.shape[1]
Out[10]: 12
# 所以将一个二维数组变为一维数组便有了如下的方法:
In [11]: a = a.reshape((a.shape[0] * a.shape[1],))
In [12]: a
Out[12]: array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
# 当然一个现成简单的方法是使用flatten这个函数
In [13]: a.flatten()
Out[13]: array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
数组的计算
# 数组直接对一个数进行加减乘除,产生的结果是数组中的每个元素都会加减乘除这个数。
In [14]: a * 2
Out[14]: array([[ 2, 4, 6],
[ 8, 10, 12],
[14, 16, 18],
[20, 22, 24]])
In [15]: a / 0
D:Anaconda3libsite-packagesipykernel\__main__.py:1: RuntimeWarning: divide by zero encountered in true_divide
if __name__ == '__main__':
Out[15]: array([[inf, inf, inf],
[inf, inf, inf],
[inf, inf, inf],
[inf, inf, inf]])
# 接下来我们看一下数组与数组之间的计算
In [17]: b = np.arange(12,24).reshape((4,3))
In [18]: b
Out[18]: array([[12, 13, 14],
[15, 16, 17],
[18, 19, 20],
[21, 22, 23]])
In [19]: a + b
Out[19]: array([[13, 15, 17],
[19, 21, 23],
[25, 27, 29],
[31, 33, 35]])
In [20]: c = np.array([1,2,3])
In [21]: a+c
Out[21]: array([[ 2, 4, 6],
[ 5, 7, 9],
[ 8, 10, 12],
[11, 13, 15]])
In [22]: d = np.arange(10,14).reshape((4,1))
In [23]: d
Out[23]: array([[10],
[11],
[12],
[13]])
In [24]: a + d
Out[24]: array([[11, 12, 13],
[15, 16, 17],
[19, 20, 21],
[23, 24, 25]])
# 从上面可以看出,和线性代数中不同的是,m*n列的m行的一维数组或者n列的一维数组也是可以计算的。
# 要求数组中所有元素的和或者每行或者每列的和应该怎么做?我们可以使用np.sum()函数
In [17]: c = a + d
In [18]: c
Out[18]: array([[11, 12, 13],
[15, 16, 17],
[19, 20, 21],
[23, 24, 25]])
In [19]: np.sum(c)
Out[19]: 216
In [20]: np.sum(c, axis = 0)
Out[20]: array([68, 72, 76])
In [21]: np.sum(c, axis = 1)
Out[21]: array([36, 48, 60, 72])
这是为什么呢?这里要提到numpy的广播原则:
如果两个数组的后缘维度(从末尾开始算起的维度)的轴长度相符或其中一方的长度为1,则认为它们是广播兼容的。广播会在缺失维度和(或)轴长度为1的维度上进行。
在上面的代码中,a的维度是(4,3),c的维度是(1,3);d的维度是(4,1)。所以假设有两个数组,第一个的维度是(x_1, y_1, z_1),另一个数组的维度是(x_2, y_2, z_2),要判断这两个数组能不能进行计算,可以用如下方法来判断:
if z_1 == z_2 or z_1 == 1 or z_2 == 1:
if y_1 == y_2 or y_1 == 1 or y_2 == 1:
if x_1 == x_2 or x_1 == 1 or x_2 == 1:
可以运算
else:
不可以运算
else:
不可以运算
else:
不可以运算
这里需要注意:(3,3,2)和(3,2)是可以运算的,因为对于二维数组(3,2)也可以表示为(1,3,2),套用上述的规则是完全适用的,同理:(4,2,5,4)和(2,1,4)也是可以进行运算的。
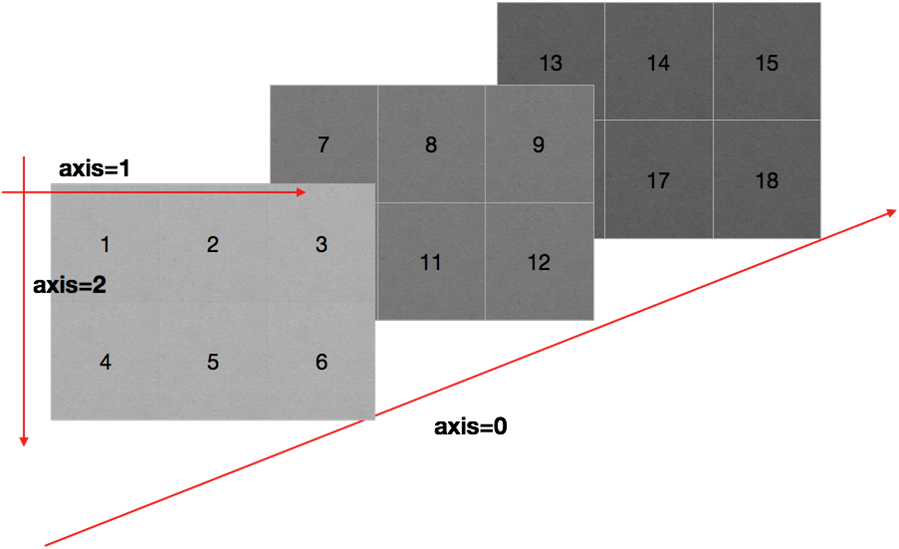
轴(axis)
在numpy中可以理解为方向,使用0,1,2...数字表示,对于一个一维数组,只有一个0轴,对于2维数组(shape(2,2)),有0轴和1轴,对于三维数组(shape(2,2, 3)),有0,1,2轴。
二维数组的轴如下图所示:

三维数组的轴:
numpy读数据
使用如下语句来读取CSV文件:np.loadtxt(fname,dtype=np.float,delimiter=None,skiprows=0,usecols=None,unpack=False)

数组转置:(两种方法)
.transpose().swapaxes(1, 0)
取数组中的值
import numpy as np
us_file_path = "./youtube_video_data/US_video_data_numbers.csv"
uk_file_path = ".youtube_video_dataGB_video_data_numbers.csv"
t1 = np.loadtxt(us_file_path, delimiter=",", dtype="int64")
print(t1)
print("*" * 100)
# 取行
# print(t1[2])
# print(t1[2,])
# 取连续的多行
# print(t1[2:])
# print(t1[2: ,])
# 取不连续的多行
# print(t1[[2, 9, 3]])
# print(t1[[2, 9, 3],])
# 取列
# print(t1[:,2])
# 取连续的多列
# print(t1[:,2:])
# 取不连续的多列
# print(t1[:, [0, 2]])
# 取元素
# print(t1[1, 3])
# 取连续多行和多列
# print(t1[1:4, 1:4])
# 取多个不相邻的点(0,1), (2, 2), (2, 3)
# print(t1[[0, 1, 2], [2, 2, 3]])
numpy中数值修改
# 取值然后赋值即可
In [1]: import numpy as np
In [2]: t2 = np.arange(24).reshape(4, 6)
In [3]: t2
Out[3]:
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])
In [4]: t2<10
Out[4]:
array([[ True, True, True, True, True, True],
[ True, True, True, True, False, False],
[False, False, False, False, False, False],
[False, False, False, False, False, False]])
In [5]: t2[t2<10] = 3
In [6]: t2
Out[6]:
array([[ 3, 3, 3, 3, 3, 3],
[ 3, 3, 3, 3, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])
In [7]: np.where(t2<10, 0, 10)
Out[7]:
array([[ 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 10, 10],
[10, 10, 10, 10, 10, 10],
[10, 10, 10, 10, 10, 10]])
clip操作
t.clip(10, 12)
# 这句话的意思是将数组t中小于10的数变为10,大于12的数变为12
拼接操作和换行换列操作
In [12]: a = np.arange(12).reshape(4,3)
In [13]: b = np.arange(12,24).reshape(4,3)
In [14]: a
Out[14]:
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]])
In [15]: b
Out[15]:
array([[12, 13, 14],
[15, 16, 17],
[18, 19, 20],
[21, 22, 23]])
# 竖直拼接
In [17]: np.vstack((a,b))
Out[17]:
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17],
[18, 19, 20],
[21, 22, 23]])
# 水平拼接
In [18]: np.hstack((a,b))
Out[18]:
array([[ 0, 1, 2, 12, 13, 14],
[ 3, 4, 5, 15, 16, 17],
[ 6, 7, 8, 18, 19, 20],
[ 9, 10, 11, 21, 22, 23]])
# 两行互换
Out[21]: 0
In [22]: a[[0,1],:] = a[[1,0],:]
In [23]: a
Out[23]:
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]])
将一维行向量转置为一维列向量的办法:.reshape(-1, 1)
构造全为0或1的包含n个元素的一维向量的方法:
# 列向量
np.zeros((n, 1))
np.ones((n, 1))
# 行向量
np.zeros((1, n))
np.ones((1, n))
numpy生成全0矩阵、全1矩阵、单位矩阵的方法以及求每行/列最大最小值的方法。
In [1]: import numpy as np
In [2]: np.zeros((4, 3))
Out[2]: array([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
In [3]: np.ones((4, 3))
Out[3]: array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
In [5]: a = np.eye(4)
In [6]: a
Out[6]: array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])
In [7]: np.argmax(a, axis = 0)
Out[7]: array([0, 1, 2, 3], dtype=int64)
In [8]: np.argmin(a, axis = 1)
Out[8]: array([1, 0, 0, 0], dtype=int64)
numpy生成随机数的方法
np.random.后加下列参数(.seed()的使用方法是先进行np.random.seed(s)再进行上述操作)
| 参数 | 解释 |
|---|---|
| .rand(d0, d1, ..., dn) | 创建d0-dn维度的均匀分布的随机数数组,浮点数,范围0-1 |
| .randn(d0, d1, ..., dn) | 创建d0-dn维度的标准正态分布随机数,浮点数,平均数0,标准差1 |
| .randint(low, high, (shape)) | 从给定上下限范围内随机取整数,形状是shape |
| .uniform(low, high, (size)) | 产生具有均匀分布的数组(浮点数),low起始值,high结束值,size形状 |
| .normal(loc, scale, (size)) | 从指定正态分布中随机抽取样本,分布中心是loc(概率分布的均值),标准差是scale,形状是size |
| .seed(s) | 随机数种子,s是给定的种子值。因为计算机生成的是伪随机数,所以通过设定相同的随机数种子,可以每次生成相同的随机数 |
numpy数组的复制
-
a = b[:]:视图的操作,会创建新的对象a,但是a的数据完全由b保管,改变b同时会引起a的改变; -
a = b.copy():复制,a和b互不影响。
In [1]: import numpy as np
In [2]: a = np.random.randint(0, 20, (4, 4))
In [3]: a
Out[3]: array([[ 1, 6, 5, 2],
[ 8, 12, 13, 8],
[19, 13, 9, 1],
[ 8, 2, 5, 5]])
In [4]: b = a[0:2,0:2]
In [5]: b
Out[5]: array([[ 1, 6, 5],
[ 8, 12, 13],
[19, 13, 9]])
In [6]: a[0, 0] = 0
In [7]: a
Out[7]: array([[ 0, 6, 5, 2],
[ 8, 12, 13, 8],
[19, 13, 9, 1],
[ 8, 2, 5, 5]])
In [8]: b
Out[8]: array([[ 0, 6, 5],
[ 8, 12, 13],
[19, 13, 9]])
nan和inf
nan(NAN,Nan):not a number表示不是一个数字,inf表示无穷大,-inf表示负无穷大。
什么时候numpy中会出现nan:当我们读取本地的值的类型为float的文件,有缺失的时候;或者当做了一个不合适的计算(比如无穷大(inf)减去无穷大)的时候,这个地方的值就会变成nan。
指定nan或者inf的方法:a[:] = np.nan;a[:] = np.inf
关于nan需要注意的地方:
-
两个nan是不相等的
-
利用(1)中的特性可以统计出一个数组中包含nan的个数
In [1]: import numpy as np
# 创建一个不含0的5阶非0方阵
In [2]: a = np.random.randint(1, 20, (5, 5))
In [3]: a
Out[3]: array([[12, 11, 2, 16, 16],
[19, 9, 7, 19, 8],
[14, 1, 2, 11, 12],
[ 5, 13, 15, 5, 13],
[ 6, 12, 4, 13, 6]])
# np.count_nonzero()这个函数用来统计数组中的非0值得个数
In [4]: np.count_nonzero(a)
Out[4]: 25
# 将数组的第3行全部变为0
In [5]: a[2,:] = 0
In [6]: a
Out[6]: array([[12, 11, 2, 16, 16],
[19, 9, 7, 19, 8],
[ 0, 0, 0, 0, 0],
[ 5, 13, 15, 5, 13],
[ 6, 12, 4, 13, 6]])
In [8]: np.count_nonzero(a)
# count_nonzero()的结果从25变为20
Out[8]: 20
# 因为nan的数值类型是float,而我们生成的数组类型为int,所以先把数组的类型转化为float
In [10]: a = a.astype(float)
# 将下面3个元素的值变为nan
In [11]: a[[1, 2, 3],[0, 3, 4]] = np.nan
In [12]: a
Out[12]: array([[12., 11., 2., 16., 16.],
[nan, 9., 7., 19., 8.],
[ 0., 0., 0., nan, 0.],
[ 5., 13., 15., 5., nan],
[ 6., 12., 4., 13., 6.]])
# 因为np.nan!=np.nan,所以在值为nan的位置会出现True,其他位置则会出现false
In [13]: a!=a
Out[13]: array([[False, False, False, False, False],
[ True, False, False, False, False],
[False, False, False, True, False],
[False, False, False, False, True],
[False, False, False, False, False]])
# 与a!=a等价的还有一种方法即np.isnan(a)他的结果也是上述这个数组
In [15]: np.count_nonzero(a!=a)
# 于是np.count_nonzero(a!=a)又可以写为np.count_nonzero(np.isnan(a))
Out[15]: 3
In [16]: (a!=a).astype(int)
# True的值即为1,False的值为0,所以non_zero()函数可以统计一个数组中包含nan的个数
Out[16]: array([[0, 0, 0, 0, 0],
[1, 0, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1],
[0, 0, 0, 0, 0]])
那么我们为什么要统计数组中nan的个数?
numpy中常用统计函数
| 类型 | 函数 |
|---|---|
| 求和 | t.sum(axis=None) |
| 均值 | t.mean(a,axis=None) 受离群点的影响较大 |
| 中值 | np.median(t,axis=None) |
| 最大值 | t.max(axis=None) |
| 最小值 | t.min(axis=None) |
| 极值 | np.ptp(t,axis=None) 即最大值和最小值之差 |
| 标准差 | t.std(axis=None) |
那么如何将数组中值为nan 的元素换为该列/行的均值?
import numpy as np
def fill_ndarray(t):
for i in range(t.shape[1]):
temp_col = t[:, i] # 当前列
nan_num = np.count_nonzero(np.isnan(temp_col)) # 计算当前列中nan的个数
if nan_num != 0:
# 计算均值
temp_non_nan_col = temp_col[temp_col == temp_col]
temp_col_mean = temp_non_nan_col.mean()
# 替换当前列中nan为均值
temp_col[np.isnan(temp_col)] = temp_col_mean
return t
a = np.arange(12).reshape(4, 3).astype(float)
a[2, 1:3] = np.nan
print(a)
print("*" * 100)
print(fill_ndarray(a))